Формируемые УУД

• Познавательные: анализировать,

делать выводы, сравнивать объекты по способам действия;

• Регулятивные: определять цель, проблему, выдвигать версии, планировать деятельность;

• Коммуникативные: излагать свое мнение, использовать речевые средства;

• Личностные: осознавать свои эмоции, вырабатывать уважительное отношение к одноклассникам

Планируемые результаты

• Предметные: умения использовать формулу для решения задач на вычисление вероятности.

• Метапредметные: умение выдвигать гипотезы, предположения, видеть

различные способы решения задачи.

• Личностные: умение правильно излагать свои мысли, понимать смысл

поставленной задачи.

Задача: Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театр мальчиков было не более 2/11 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 2/5 от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 9 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?

Разбор задания:

Сначала разберемся с условием:

(Параллельно с объяснением учитель все изображает на доске).

Предположим, что у нас есть множество ребят, которые сходили в кино, и множество ребят, которые сходили в театр. Т.к. сказано, что они все сходили, то вся группа входит или в множество ребят, которые сходили в театр, или в множество ребят, сходивших в кино. Что обозначает место, где эти множества пересекаются?

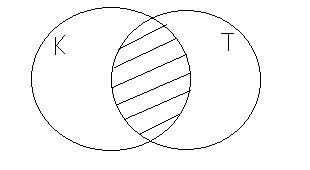
Оно обозначает, что эти ребята сходили и в кино и в театр одновременно.

Известно, что мальчиков, сходивших в театр, было не более 2/11 от общего числа сходивших в театр всего. Учитель просит кого-нибудь из учеников изобразить это на доске.

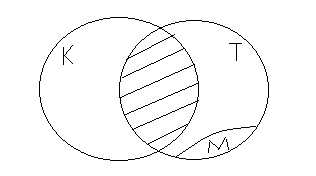
А мальчиков, которые сходили в кино могло быть больше - не более 2/5 от общего числа учащихся группы.

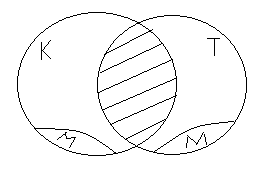
Теперь перейдем к решению.

а) У нас имеется 9 мальчиков, всего учащихся, обозначим N=20, должны выполняться все условия. Если у нас мальчиков 9, девочек, соответственно, 11. Пункт а) можно решить в большинстве случаев перебором.

Предположим, что у нас мальчики ходили либо только в кино, либо в театр.

А девочки сходили туда и туда. (Синим показано множество мальчиков, а черная штриховка - девочки)

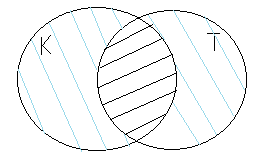
Так как у нас всего 9 мальчиков и, по условию, в театр сходило меньше мальчиков, предполагаем, что в театр сходило 2 мальчика, а в кино – 7. И посмотрим, выполняется ли наше условие.

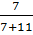
Проверим сначала на примере театра. Берем число мальчиков, сходивших в театр, ко всем, кто сходил в театр и плюс число девочек и сравним это с : 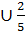. Домножим это на 18 и на 5: .

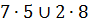, следовательно дробь 7/18 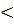2/5. Значит, условие выполняется для кино.

Теперь посмотрим, выполняется ли это условие для театра. Самостоятельно, потом кто-то из учеников записывает решение на доске.

Ответ: Если группа состоит из 2 мальчиков, посетивших только театр, 7 мальчиков, посетивших только кино, и 11 девочек, сходивших и в театр, и в кино, то условие задачи выполнено. Значит, в группе из 20 учащихся могло быть 9 мальчиков.

б) Предположим, что мальчиков было 10 или больше. Тогда девочек было 10 или меньше. Театр посетило не более 2 мальчиков, поскольку если бы их было 3 или больше, то доля мальчиков в театре была бы не меньше 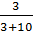= 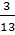, что больше .

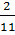Аналогично, кино посетило не более 7 мальчиков, поскольку 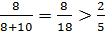, но тогда хотя бы один мальчик не посетил ни театра, ни кино, что противоречит условию.

В предыдущем пункте было показано, что в группе из 20 учащихся могло быть 9 мальчиков. Значит, наибольшее количество мальчиков в группе — 9.

в) Предположим, что некоторый мальчик сходил и в театр, и в кино. Если бы вместо него в группе присутствовало два мальчика, один из которых посетил только театр, а другой — только кино, то доля мальчиков и в театре, и в кино осталась бы прежней, а общая доля девочек стала бы меньше. Значит, для оценки наименьшей доли девочек в группе можно считать, что каждый мальчик сходил или только в театр, или только в кино.

Пусть в группе 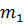мальчиков, посетивших театр, 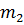мальчиков, посетивших кино, и d девочек.

Оценим долю девочек в этой группе. Нулем считать, что все девочки ходили и в театр, и в кино, поскольку их доля в группе от этого не изменится, а доля в театре и в кино не уменьшится.

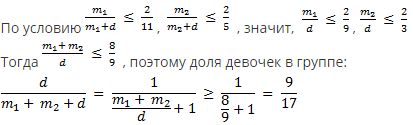
Если группа состоит из 2 мальчиков, посетивших только театр, 6 мальчиков, посетивших только кино, и 9 девочек, сходивших и в театр, и в кино, то условие задачи выполнено, а доля девочек в группе равна .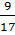

Date: 2015-06-08; view: 777; Нарушение авторских прав