
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теория вероятностей
|
|
В повседневной жизни, в практической и научной деятельности мы часто наблюдаем те или иные явления, проводим определенные эксперименты.
Событие, которое может произойти, а может и не произойти в процессе наблюдения или эксперимента, называют случайным событием. Например, под потолком висит лампочка – никто не знает, когда она перегорит. Каждое случайное событие - есть следствие действия очень многих случайных величин (сила, с которой брошена монета, форма монеты и многое другое). Невозможно учесть влияние на результат всех этих причин, так как число их велико и законы действия неизвестны.Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей.
Теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет - она просто не в силах это сделать. Если же речь идет о массовых однородных случайных событиях, то они подчиняются определенным закономерностям, а именно вероятностным закономерностям.
Для начала давайте рассмотрим классификацию событий.
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие A — выпадание трех очков на первой игральной кости, событие B — выпадание трех очков на второй кости. A и B — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие A — наудачу взятая коробка окажется с обувью черного цвета, событие B — коробка окажется с обувью коричневого цвета, A и B — несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.
Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера. A — появление красного шара при одном извлечении, B — появление белого шара, C — появление шара с номером. События A,B,C образуют полную группу совместных событий.
Событие может быть противоположным, или дополнительным. Под противоположным событием 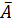 понимается событие, которое обязательно должно произойти, если не наступило некоторое событие A. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие A, либо бракованным — событие
понимается событие, которое обязательно должно произойти, если не наступило некоторое событие A. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие A, либо бракованным — событие 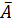 .
.
Рассмотрим пример. Бросают игральный кубик (т.е. небольшой куб, на гранях которого выбиты очки 1, 2, 3, 4, 5, 6). При бросании игрального кубика на его верхней грани может выпасть одно очко, два очка, три очка и т.д. Каждый из этих исходов является случайным.
Провели такое испытание. Игральный кубик бросали 100 раз и наблюдали, сколько раз произойдет событие «на кубике выпало 6 очков». Оказалось, что в данной серии экспериментов «шестерка» выпала 9 раз. Число 9, которое показывает, сколько раз в этом испытании произошло рассматриваемое событие, называют частотой этого события, а отношение частоты к общему числу испытаний, равное  , называют относительной частотой этого события.
, называют относительной частотой этого события.
Вообще пусть определенное испытание проводится многократно в одних и тех же условиях и при этом каждый раз фиксируется, произошло или нет интересующее нас событие A. Вероятность события обозначается большой латинской буквой P. Тогда вероятность события А будем обозначать: Р(А).
Классическое определение вероятности:
Вероятность события A равна отношению числа случаев m, благоприятствующих ему, из общего числа n единственно возможных, равновозможных и несовместных случаев к числу n, т. е.
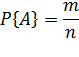
Следовательно, для нахождения вероятности события необходимо:
1. рассмотреть различные исходы испытаний;
2. найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать их общее число n, число случаев m, благоприятствующих данному событию;
3. выполнить расчет по формуле.
Из формулы следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев:
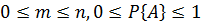
Рассмотрим еще один пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым. Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С. Тогда в соответствием с записанными выше формулами получаем:
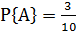 ;
; 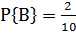 ;
; 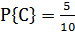
Отметим, что вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.
Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов. Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:
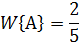
Как видно, эта величина не совпадает с найденной вероятностью. При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события.
Геометрическая вероятность. Классическое определение вероятности предполагает, что число элементарных исходов конечно, что также ограничивает его применение на практике.
В случае, когда имеет место испытание с бесконечным числом исходов, используют определение геометрической вероятности – попадание точки в область.
| M |
| N |
Событие A – «попадание брошенной точки на область M». Область M называют благоприятствующей событию A.
Вероятность попадания в какую-либо часть области N пропорциональна мере этой части и не зависит от ее расположения и формы.
| N |
| M |
1. отрезок (мерой является длина)
2. геометрическая фигура на плоскости (мерой является площадь)
3. геометрическое тело в пространстве (мерой является объем)
Дадим определение геометрической вероятности для случая плоской фигуры.
Пусть область M является частью области N. Событие A состоит в попадании случайно брошенной на область N точки в область M. Геометрической вероятностью события A называется отношение площади области M к площади области N:
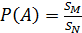
При этом вероятность попадания случайно брошенной точки на границу области считается равной нулю.
Рассмотрим пример: Механические часы с двенадцатичасовым циферблатом сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 5, но не дошла до отметки 8 часов.
Решение. Число исходов бесконечно, применим определение геометрической вероятности. Сектор между 5 и 8 часами составляет  часть площади всего циферблата, следовательно,
часть площади всего циферблата, следовательно, 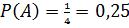 .
.
Операции над событиями:
События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.
Объединением или суммой событий 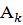 называется событие A, которое означает появление хотя бы одного из событий
называется событие A, которое означает появление хотя бы одного из событий 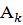 .
.
A= 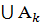
Пересечением или произведением событий 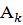 называется событие А, которое заключается в осуществлении всех событий
называется событие А, которое заключается в осуществлении всех событий 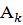 .
.
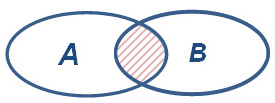 Произведение совместных событий Произведение совместных событий
|
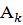
Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.
Пример:
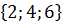 B – «на кубике выпало число, делящееся на 3»
B – «на кубике выпало число, делящееся на 3» 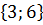
|
A + B – «выпало 2; 4; 6 или 3 очка»
A ∙ B – «выпало 6 очков»
A – B – «выпало 2 и 4 очка»
Дополнительным к событию А называется событие 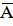 , означающее, что событие А не происходит.
, означающее, что событие А не происходит.
Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.
Совокупность всех элементарных исходов опыта называется пространством элементарных событий.
Свойства вероятностей:
Свойство 1. Если все случаи являются благоприятствующими данному событию A, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления 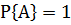 , так как в этом случае
, так как в этом случае
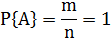
Свойство 2. Если нет ни одного случая, благоприятствующего данному событию A, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления  , так как в этом случае m=0:
, так как в этом случае m=0:
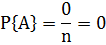
Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.
Свойство 4. Вероятность наступления противоположного события  определяется так же, как и вероятность наступления, события A:
определяется так же, как и вероятность наступления, события A:
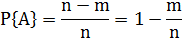
где (n-m) — число случаев, благоприятствующих появлению противоположного события 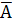 . Отсюда вероятность наступления противоположного события
. Отсюда вероятность наступления противоположного события 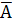 равна разнице между единицей и вероятностью наступления события A:
равна разнице между единицей и вероятностью наступления события A:
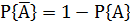
Сложение и умножение вероятностей.
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем A⊂B.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей 1. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
P 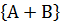 =P
=P 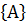 +P
+P 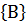
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
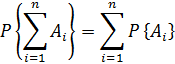
Если случайные события 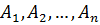 образуют полную группу несовместных событий, то имеет место равенство
образуют полную группу несовместных событий, то имеет место равенство
P 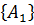 +P
+P 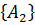 +…+P
+…+P 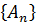 =1
=1
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
P 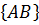 =P
=P 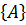 +P
+P 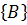 -P
-P 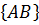
Date: 2015-06-08; view: 1329; Нарушение авторских прав