
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ПРИЛОЖЕНИЕ. Обратимся к некоторым примерам использования дифференциального исчисления для строгого подсчета излишка потребителя
|
|
Обратимся к некоторым примерам использования дифференциального исчисления для строгого подсчета излишка потребителя. Начнем с задачи нахождения максимума квазилинейной функции полезности:
max v(x)+y
x,y
при px+y=m.
После подстановки из бюджетного ограничения выражения для y получаем
max v(x)+m-px.
x
Условие первого порядка для данной задачи имеет вид
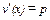 .
.
Это означает, что обратная функция спроса p(x) определяется уравнением
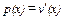 (14.2) (14.2)
|
Обратите внимание на аналогию с описанным в тексте решением подобной задачи для случая дискретного товара: цена, при которой потребитель как раз готов потребить x единиц товара, равна предельной полезности.
Однако, поскольку обратная функция спроса дает нам величину производной функции полезности, чтобы найти функцию полезности, можно просто проинтегрировать обратную функцию спроса.
Производя интегрирование, мы получаем:
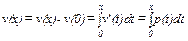 .
.
Следовательно, полезность, связываемая с потреблением товара x, есть не что иное как площадь под кривой спроса.
ПРИМЕР: Несколько функций спроса
Предположим, что функция спроса линейна, так что x(p)=a-bp. Тогда изменение излишка потребителя при движении цены от p до q задано выражением
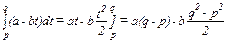 .
.
Другая широко используемая функция спроса, которую мы более детально изучим в следующей главе, имеет вид 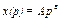 , где
, где 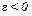 и A — некая положительная константа. При изменении цены от p до q связанное с этим изменение излишка потребителя составляет
и A — некая положительная константа. При изменении цены от p до q связанное с этим изменение излишка потребителя составляет
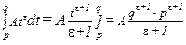 ,
,
для 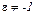 .
.
При 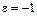 эта функция спроса имеет вид x(p)=A/p,что очень похоже на хорошо известную нам функцию спроса Кобба-Дугласа, x(p)=am/p. Изменение излишка потребителя для функции спроса Кобба-Дугласа есть
эта функция спроса имеет вид x(p)=A/p,что очень похоже на хорошо известную нам функцию спроса Кобба-Дугласа, x(p)=am/p. Изменение излишка потребителя для функции спроса Кобба-Дугласа есть
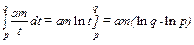 .
.
Табл.14.1 Сравнение CV, CS и EV.
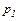
| CV | CS | EV |
| 0,00 | 0,00 | 0,00 | |
| 7,18 | 6,93 | 6,70 | |
| 11,61 | 10,99 | 10,40 | |
| 14,87 | 13,86 | 12,94 | |
| 17,46 | 16,09 | 14,87 |
ПРИМЕР: CV, EV и излишек потребителя
В тексте нами были подсчитаны компенсирующие и эквивалентные вариации дохода для функции полезности Кобба-Дугласа. В предыдущем примере мы подсчитали изменение излишка потребителя для функции полезности Кобба-Дугласа. Здесь мы сравниваем между собой эти три денежных меры влияния, оказываемого на полезность изменением цены.
Допустим, что цена товара 1 изменяется от 1 до 2, 3 и т.д., в то время как цена товара 2 остается без изменений на уровне 1, а величина дохода неизменна и равна 100. В табл.14.1 показаны эквивалентная вариация дохода (EV), компенсирующая вариация дохода (CV) и изменение излишка потребителя (CS) для функции полезности Кобба-Дугласа 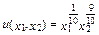 .
.
Обратите внимание на то, что величина изменения излишка потребителя всегда находится между величинами CV и EV и что разница между этими тремя числами относительно мала. Можно показать, что оба указанных факта наблюдаются при достаточно общих условиях.
[1]Конечно,изменение излишка потребителя — это лишь один из способов, которыми можно представить изменение полезности, — изменение величины, равной квадратному корню из излишка потребителя, могло бы столь же успешно служить способом указанного измерения. Однако, использование излишка потребителя в качестве стандартной меры полезности является общепринятой нормой.
Date: 2015-06-08; view: 520; Нарушение авторских прав