
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 7 Приложения производной
|
|
Правило Лопиталя ('без вывода), Теорема Ролля и Лагранжа (с нестрогими геометрическими доказательствами). Признаки возрастания и убывания функции. Экстремум функции. Необходимые и достаточные признаки экстремума (второй достаточный признак – без доказательства). Исследование функции (область определения, четность и нечетность, интервалы монотонности и точки экстремума, поведение функции при х ®±¥ и в точках разрыва, горизонтальные и вертикальные асимптоты, точки пересечения графика с осями координат) и построние ее графика. Квадратичная функция у = ax2+bx+c и ее график. Дробно-линейная функция у = 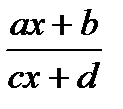 и ее график. (1, гл. 8, § 8.1 – 8.5, 8.7 – 8.9; с. 205–21, 225–236); (2, гл. 8).
и ее график. (1, гл. 8, § 8.1 – 8.5, 8.7 – 8.9; с. 205–21, 225–236); (2, гл. 8).
Нужно уяснить, что правило Лопиталя является эффективным средством вычисления пределов. При этом нужно понимать, что предел отношения двух бесконечно малых или бесконечно больших функций заменяется вычислением отношения их производных. Это правило можно использовать для вычисления целого ряда неопределенностей.
С помощью производных можно эффективно исследовать функции на возрастание и убывание, определять экстремумы функций (1,с.216, 217), наибольшее и наименьшее значение. Для этого необходимо знать теоремы о достаточных условиях возрастания и убывания функции, определения точек минимума и максимума, первое и второе достаточное условие экстремума, определение выпуклости и вогнутости функции (выпуклости вниз). Необходимо знать общую схему исследования функции, кроме п.6,7 (1, с.232).
В учебном пособии приведена схема исследования функции для нахождения характерных точек и особенностей, по которым можно построить ее график (1, с. 232). Выполнение пункта 6' этой схемы, связанного с нахождением интервалов выпуклости функции и точек перегиба, в программу не входит.
Рекомендуется разобрать задачи с решениями е 8.1–8.3, 8.4–8.7; 8.9, 8.11–8.15, 8.17 и задачи для самостоятельной работы N 8.19–8.31, 8.32–8.34, 8 41–8.53 по учебнику (1) и аналогичные задачи по практикуму (2), обратив особое внимание на исследование функций и построение их графиков.
Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
| Начальная буква фамилии | Вариант задания |
| А, Е, Л | Первый |
| Р, Х, Э | Второй |
| Б, Ж, М | Третий |
| С, Ц, Ю | Четвертый |
| В, З, Н | Пятый |
| Т, Ч | Шестой |
| Г, И, О | Седьмой |
| У, Ш | Восьмой |
| Д, К, П | Девятый |
| Ф, Щ, Я | Десятый |
Date: 2015-06-08; view: 531; Нарушение авторских прав