Тема 2 Система линейных уравнений

Система n линейных уравнений с n переменными (общий вид). Матрица системы. Матричная форма записи системы. Совместные (определенные и неопределенные) и несовместные системы. Теорема Крамера о разрешимости системы n линейных уравнений с n переменными (без доказательства). Решение системы: по формулам Крамера; с помощью обратной матрицы; методом Гауса. (1, гл. 2, §2.1—2.3,2.6; с. 38—47,53—56); (2, гл. 2).

При изучении материала темы следует освоить матричную форму записи заданной системы п линейных уравнений с п переменными и уметь переходить к этой форме от общего вида системы и наоборот. Необходимо знать и уметь объяснить, какие системы уравнений называются совместными (определенными и неопределенными) и несовместными. Надо твердо уяснить, что вопрос о разрешимости системы n линейных уравнений с n переменными устанавливается с помощью теоремы Крамера (1, с. 41); решаются же такие системы различными способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса (см. примеры 2.1 – 2.3, 2.6, 2.7).

Наиболее важен для практики метод Гаусса, имеющий по сравнению с другими способами решения ряд достоинств: он менее трудоемок, позволяет однозначно установить, является ли данная система определенной, неопределенной или несовместной, а в случае совместности системы – определить число ее независимых уравнений и исключить «лишние».

В методе Гаусса нужно усвоить правило исключения неизвестных х₁, х₂, …, х_n-1. Сначала умножается первая строка на соответствующие коэффициенты. Цель – в первом столбце во всех строках кроме первой обеспечить нули путем прибавления первой строки, умноженной на коэффициенты, ко второй и последующим строкам.

Затем умножается вторая строка на соответствующие коэффициенты. Цель – обеспечить нули во втором столбце во всех строках кроме второй (a₂₂ ¹0) путем прибавления к третьей и последующим строкам второй строки, умноженной на необходимые коэффициенты и т.д.

Для первой строки это коэффициенты (-a₂₁/a₁₁;-a₃₁/a₁₁;…;-a_m1/a₁₁); для второй строки это коэффициенты (-a₃₂/a₂₂;-a₄₂/a₂₂;…;-a_m2/a₂₂).

Необходимо понять, что при прямом ходе решения системы уравнений методом Гаусса определяется неизвестное х_n. Затем при обратном ходе определяются х_n-1, х_n-2 и так до х₁.

Необходимо уяснить, что метод Гаусса менее трудоемок особенно при решении систем уравнений более четвертого порядка.

Следует обратить внимание на различие между основными или базисными переменными, для которых определитель матрицы из коэффициентов при них отличен от нуля (х₁,х₂,…,х_r—переменные). Остальные (n–r) переменных называются не основными или свободными.

Необходимо усвоить, что для базисных решений должны быть равны нулю все (n-r) не основных переменных, и что число базисных решений имеется не более С_n^r = .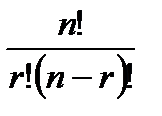

Необходимо разобраться (теорема Кронекера-Капелли) в том, что система имеет единственное решение в том случае, когда ранг матрицы «r» равен числу переменных «n», т.е. r=n; система имеет бесконечное множество решений, если n >r.

Необходимо разобраться в алгоритме нахождения базисных решений, а именно: научиться находить все определители, не равные нулю, которые и составляются из коэффициентов при основных (базисных) переменных, выражать основные (базисные) решения через не основные. Иметь понятие о функциональной системе решений для системы линейных однородных уравнений.

Рекомендуется разобрать задачи с решениями N 2.1 – 2.3, 2.6, 2.7 и задачи ля самостоятельной работы N 2.11, 2.12, 2.15 – 2.18, 2.21 – 2.23 по учебнику [1] и аналогичные задачи по практикуму [2].

Date: 2015-06-08; view: 492; Нарушение авторских прав