
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Операции с вещественными числами
|
|
Операции сложения и вычитания вещественных чисел.
Вещественные числа в компьютерах представляются в форматах с плавающей запятой (точкой), т.е. в полулогарифмическом виде. В связи с этим, операциям сложения и вычитания могут подвергаться только числа с одинаковыми порядками. Следовательно, первой же предварительной операцией перед сложением или вычитанием должна осуществляться операция выравнивания порядков. Выравнивание осуществляется по старшему порядку операндов для сохранения значения мантисс меньше 1. При выравнивании порядков значение большего порядка присваивается значению порядка меньшего числа, при этом для сохранения величины самого числа, его мантисса сдвигается вправо на число разрядов, равное разнице между порядками операндов.
После выравнивания порядков, мантиссы операндов рассматриваются как целые числа со знаком и, операции сложения и вычитания в дальнейшем осуществляются в соответствии с алгоритмом аналогичных операций для целых чисел со знаком. Следует только иметь в виду, что в отличие от отрицательных целых чисел, которые хранятся в памяти в дополнительном коде, мантиссы вещественных отрицательных чисел всегда хранятся в памяти в прямом коде. И преобразование прямого кода мантисс в дополнительный код у отрицательных чисел, осуществляется перед осуществлением операции, непосредственно в арифметико-логическом устройстве сопроцессора.
Отметим также, что отличием проведения операций сложения и вычитания мантисс от проведения аналогичных операций с целыми числами, является то, что появления признака переполнения разрядной сетки не рассматривается как признак недостоверности результата. Он рассматривается просто как сигнал, по которому значение мантиссы результата сдвигается вправо на один разряд, увеличивая, одновременно, на один разряд значение его порядка. Дело в том, что мантисса есть дробная часть числа, и отбрасывание ее младшего разряда, которое происходит при сдвиге мантиссы вправо, приводит лишь к уменьшению точности представления результата на значение этого разряда, т.е. приводит к той точности, которая задана величиной разрядной сетки представления мантиссы результата. Тем более что все эти операции происходят в сопроцессоре при представлении операндов в 80 – разрядном формате временных вещественных чисел.
Однако следует учесть, что это не относится к случаям при операциях с порядками, осуществляемых при умножении и делении.. Если в результате операции с порядками произойдет переполнение разрядной сетки, то результат окажется недостоверным.
Таким образом, операции сложения вещественных чисел осуществляется по следующему алгоритму.
1. Операнды из оперативной памяти компьютера пересылаются в сопроцессор, с явным отображением «скрытой» 1 в старшем разряде ее мантиссы.
2. Порядки операндов выравниваются по порядку большего числа, с соответствующим сдвигом мантиссы меньшего числа вправо на количество разрядов, равное разницы значений порядков.
3. Мантиссы отрицательных чисел представляются в дополнительном коде.
4. Коды мантисс, совместно со знаковыми разрядами, суммируются как целые числа со знаками.
5. При переполнении разрядной сетки, код результата сдвигается вправо на один разряд, при этом значение порядка увеличивается на единицу.
6. Если результат получился отрицательным, мантисса результата, будет представлена в дополнительном коде. А поскольку в памяти компьютера мантиссы всех вещественных чисел хранятся только в прямых кодах, то производится преобразование ее дополнительного кода в прямой код.
7. При получении ненормализованного результата (т.е. получении в старших разрядах мантиссы результата - нулей) код мантиссы результата сдвигается влево до появления 1 в ее старшем разряде. При этом для сохранения значения результата, порядок его уменьшается на количество сдвигов мантиссы. Т.е. происходит нормализация полученного результата.
8. Полный результат операции, со знаковым разрядом, скорректированным порядком и мантиссой, представленной в прямом коде, без «скрытой» единицы старшего разряда, передается в оперативную память компьютера.
Алгоритм вычитания вещественных чисел отличается только пунктом 4, в котором осуществляется суммирование кода мантиссы уменьшаемого, с дополнительным кодом вычитаемого. При этом дополнительный код вычитаемого формируется из прямого кода, вместе с его знаковым разрядом.
Приведем пример последовательности выполнения в компьютере операции вычитания вещественных чисел.
Пример:
Пусть: А = - 6,2510; В = + 0,187510; Формат хранения чисел: короткое вещественное, порядок – смещенный с отрицательным нулем.
Рассмотрим порядок проведения операции (А – В). (В результате проведенной операции должно получиться число: – 6,437510).
Полулогарифмическое двоичное представление заданных чисел будет иметь вид:
А = - 110,01 = - 2+10∙1,1001; В = + 0,0011 = + 2-11∙1,1;
В формате КВ, порядок – 8-ми разрядный, следовательно, смещение для получение смещенного порядка с отрицательным нулем будет равно: 01111111. Тогда, смещенный порядок числа А будет: 01111111 + 10 = 10000001, а смещенный порядок числа В будет: 01111111 – 11 = 01111100.
Таким образом, представление приведенных выше чисел, в основной памяти, (учитывая, что старший разряд мантиссы является «скрытым» разрядом, и в основной памяти не хранится) будет иметь вид:
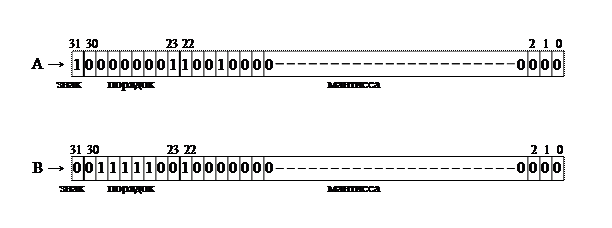
Сами операции с вещественными числами осуществляются только в математическом сопроцессоре, в 80-ти разрядном формате ВВ, который содержит разряд знака, 15 разрядов порядка и 64 разряда мантиссы. При этом в формате ВВ, старший «скрытый» разряд мантиссы делается явным. В формате ВВ, порядок – 15-ти разрядный, следовательно, смещение для получение смещенного порядка с отрицательным нулем будет равно: 011111111111111. Тогда, смещенный порядок числа А будет: 011111111111111 + 10 = 100000000000001, а смещенный порядок числа В будет: 011111111111111 – 11 = 011111111111100.
Следовательно, числа А и В, переданные в сопроцессор и преобразованные в формат ВВ будут иметь вид:
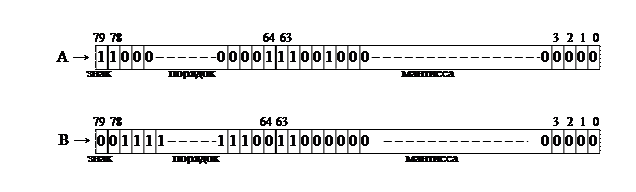
Перед тем как осуществлять операцию, необходимо, прежде всего, произвести выравнивание порядков чисел, по числу со старшим порядком (в нашем примере, по порядку числа А). Число В, с выровненным порядком, в формате ВВ, будет иметь следующий вид.
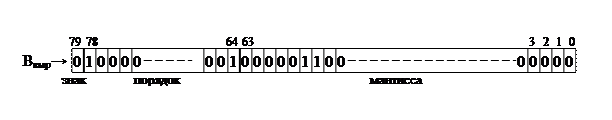
Затем, поскольку число А отрицательное, то для возможности дальнейшего осуществления с мантиссами, как целыми числами со знаком, мантисса числа А представляется в дополнительном коде.
Прямой код мантиссы числа А: 1100100.……………0.
Дополнительный код мантиссы числа А: 0011100……..0.
Следовательно, вместе со знаковыми разрядами, мантиссы чисел А и В, будут иметь следующие коды.
Код мантиссы числа А со знаком: 100111000……………0.
Код мантиссы числа В со знаком: 000000110……………0.
Операция вычитания мантисс А и В сводится к суммированию кодов мантиссы числа А со знаком, с дополнительным кодом мантиссы числа В со знаком. Для этого, прежде всего, формируется дополнительный код мантиссы числа В со знаком.
Прямой код мантиссы числа В со знаком: 000000110…………….0.
Дополнительный код мантиссы числа В со знаком: 1111110100…..00.
После этого осуществляется операция сложения прямого кода мантиссы со знаком числа А, с дополнительным кодом мантиссы со знаком числа В, рассматриваемых как целые числа со знаком.
100111000………………0
+
111111010………………0
----------------------------------------
1: 100110010………………0
Поскольку при осуществлении операции был перенос, как в знаковый разряд, так и из знакового разряда, то переполнения разрядной сетки нет, флаг OF = 0, и результат является достоверным. Кроме того, поскольку знаковый разряд равен 1, то это означает, что результат получился отрицательным, флаг SF = 1 и, следовательно, значение результата представлено в дополнительном коде.
Однако в основную память мантисса должна быть передана в прямом коде. Поэтому полученный результат преобразуется в прямой код.
Дополнительный код значения результата (без знака): 00110010………….0.
Прямой код значения результата (без знака): 1100111000…………..0.
Следовательно, в формате ВВ результат будет представлен в виде:
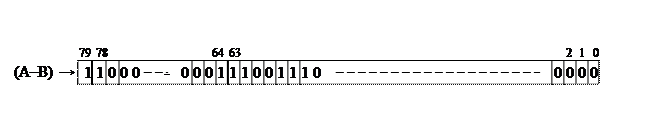
Поскольку старшие разряды мантиссы не равны нулю, то нормализация результата не производится.
Затем, результат из формата ВВ преобразуется в формат КВ со скрытым старшим разрядом мантиссы. Таким образом, результат, переданный в основную память компьютера, будет равен:

Несмещенный (исходный) порядок результата получается путем вычитания значения смещения из полученного смещенного порядка:
10000001 – 01111111 = 00000010.
Следовательно, окончательный результат рассмотренной операции вычитания двух вещественных чисел равен:
− 2+10∙1,100111 = − 110,01112 = − 6,437510
Основные принципы осуществления операций умножения и деления
вещественных чисел.
При осуществлении операций умножения вещественных чисел, порядки сомножителей суммируются, а мантиссы перемножаются. Произведение нормализуется и ему присваивается знак плюс, если сомножители имеют одинаковые знаки, и знак минус, если знаки разные. Если мантисса множимого или множителя равна нулю, то произведению присваивается значение 0 без выполнения умножения мантисс.
При делении вещественных чисел мантисса частного равна частному от деления мантиссы делимого на мантиссу делителя, а порядок частного – разности порядков делимого и делителя. Частное нормализуется, и ему присваивается знак плюс, если делимое и делитель имеют одинаковые знаки, и знак минус, если знаки разные. Если делимое равно 0, то в частное записывается 0 без выполнения деления. Если делитель равен 0, то деление не производится и формируется сигнал прерывания.
Date: 2015-05-04; view: 2448; Нарушение авторских прав