
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

VI. Основы компьютерной арифметики
|
|
Обработка числовой информации по сколь-угодно сложным алгоритмам, вычисление сложнейших математических выражений (решение нелинейных и трансцендентных уравнений, решение систем линейных и нелинейных с огромным числом неизвестных, решение дифференциальных уравнений обычных и в частных производных, и их систем и т.п.), а также моделирование сложнейших процессов и явлений, мультимедийные построения, все это, в конечном счете, осуществляются в компьютерах с помощью обычных четырех действий арифметики.
Сведение же решения всех этих указанных задач к четырем арифметическим действиям является основной целью вычислительной математики, в настоящее время самостоятельной области математической науки. Реализация этих алгоритмов осуществляется с помощью программного обеспечения компьютера.
Обработка числовой информации в компьютере, в подавляющем большинстве случаев, осуществляется в двоичной системе счисления, поскольку основная форма представления чисел в них – двоичная. Напомним основные правила двоичной арифметики и, используемых при обработке, основных логических функциях.
Арифметические операцииЛогические операции
сложение конъюнкция дизъюнкция
0 + 0 = 0 0 & 0 = 0 0 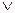 0 = 0
0 = 0
0 + 1 = 1 0 & 1 = 0 0 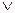 1 = 1
1 = 1
1 + 0 = 1 1 & 0 = 0 1 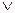 0 = 1
0 = 1
1 + 1 = 0 → (перенос) 1 & 1 = 1 1 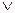 1 = 1
1 = 1
Вычитание инверсия неравнозначность
0 – 0 = 0 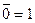
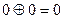
0 – 1 = 1→ (заем) 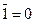
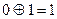
1 – 0 = 1 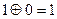
1 – 1 = 0 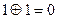
При выполнении арифметических операций умножения и деления необходима еще операция сдвига кодов.
Напомним, что логические операции с многоразрядными двоичными числами выполняются поразрядно, т.е. в каждом разряде отдельно, независимо друг от друга. Что касается арифметических операций с многоразрядными числами, то надо иметь в виду, что правило их выполнения во всех во всех позиционных системах счисления аналогичны. Поэтому правила осуществления арифметических операций с многоразрядными двоичными числами, аналогичны правилам осуществления арифметических операций с многоразрядными десятичными числами.
Кроме самого результата операции, в процессорах компьютеров фиксируется ряд признаков, характеризующих полученный результат. Их состояние отображается появлением 0 или 1 в соответствующем разряде специального регистра, называемого регистром флагов (признаков). Появление в таком разряде 1, называют установкой соответствующего флага. Обычно отображаются 6 основных признаков (флагов) осуществления арифметических операций:
· Перенос из старшего разряда результата (устанавливается в 1 флаг CF – Carry Flag). Используется процессором при осуществлении сдвиговых операций, а также как признак переполнения разрядной сетки при операции сложения целых чисел без знака (при операции вычитания служит признаком получения отрицательного результата). Является также аргументом при исполнении соответствующих команд условных переходов. Кроме того, этот флаг используется процессором при операциях с числами, разрядность которых превышает разрядность текущих регистров процессора, например, при необходимости операций с 64 разрядными числами в процессорах архитектуры IA-32, т.е. в процессорах, разрядность регистров которых равна 32 битам. В этом случае состояние этого флага, после проведения операции с младшими 32 разрядами числа, суммируется с результатом последующей операции над старшими разрядами этого числа.
· Четность числа единиц в коде младшего байта результата (устанавливается в 1 флаг PF – Parity Flag). Используется этот флаг процессором для контроля правильности передачи кодов, а также как аргумент при исполнении соответствующих команд условных переходов.
· Перенос из первой тетрады младшего байта результата в его старшую тетраду (устанавливается в 1 флаг AF – Auxiliary Flag). Флаг используется процессором только при обработке двоично-десятичных кодов, вводя соответствующую коррекцию в полученный результат.
· Признак нулевого результата (устанавливается в 1 флаг ZF – Zero Flag). Процессором этот флаг используется как аргумент при исполнении соответствующих команд условного перехода.
· Признак отрицательного результата (устанавливается в 1 флаг SF – Sign Flag). Этот флаг определяет результат как представленный в дополнительном коде, а также используется процессором как аргумент при исполнении команд условного перехода. При операциях с целыми числами без знака, установка флага SF в 1 говорит о том, что уменьшаемое меньше вычитаемого.
· Признак переполнения разрядной сетки (устанавливается в 1 флаг OF – Overflow Flag). Определяется как функция неравнозначности переносов в знаковый разряд результата и из знакового разряда. Используется процессором при обработке двоичных чисел со знаком, а также в командах умножения и деления.
Арифметические операции с числами можно разделить на следующие группы операций.
1. Операции с целыми двоичными и двоично-десятичными числами:
а) операции с целыми двоичными и двоично-десятичными числами без знака (адресами, номерами, содержимым счетчиков, кодами команд, символами и т.п.);
б) операции с целыми двоичными числами со знаком (целые двоично-десятичные числа со знаком используются крайне редко).
2. Операции с вещественными двоичными числами (вещественные числа в двоично-десятичном формате используются крайне редко).
Date: 2015-05-04; view: 942; Нарушение авторских прав