Операции сложения и вычитания целых чисел

Операции сложения и вычитания целых чисел без знака.

При осуществлении операций с двоичными целыми числами без знака используется обычная двоичная арифметика, включающая как операцию сложения, так и операцию вычитания, используя только прямые коды чисел. Поскольку операции умножения и деления сводятся к операциям сложения, вычитания и сдвига, то это также справедливо и для них. При этом перенос из старшего разряда при сложении и заем при вычитании сопровождается установкой в 1 флага CF. При сложении, это характеризует переполнение разрядной сетки, а при вычитании – получения отрицательного результата. В этом последнем случае, результат получается представленным в дополнительном коде. Переполнения разрядной сетки при операции вычитания не может быть принципиально.

Отметим, при этом, что при операциях сложения и вычитания целых чисел без знака, флаг OF не определен.

Примеры:

1. 11011011: В результате операции произошел перенос из старшего разряда.

+

10100011: Следовательно, произошло переполнение разрядной сетки и

--------------: результат является недостоверным. (219 + 163 = 382).

1: 01111110: Состояние флагов: ZF=0; AF=0; PF=1; CF=1;

2. 10011001: Переноса из старшего разряда нет, результат достоверный. (153+99=252).

+: Состояние флагов: ZF=0; AF=0; PF=1; CF=0:

01100011:

--------------:

11111100:

3. 11010101: Результат положителен и представлен в прямом коде.(213 – 178 = 35).

-: Состояние флагов: ZF=0; AF=0; PF=0; CF=0.

10110010:

-------------

00100011:

4. 10101110: Перенос из старшего разряда свидетельствует о том, что уменьшаемое

-: меньше вычитаемого. (Можно сказать, что результат является как бы

11000110: отрицательным, и представлен в дополнительном коде)

(174 – 198 = −24).

---------------: Состояние флагов: ZF=0; AF=0; PF=1; CF=1.

1: 11101000:

Особенности операций сложения и вычитания в компьютерах

двоично-десятичных чисел без знака.

Операции с двоично-десятичными числами осуществляются на тех же сумматорах, на которых осуществляются операции с двоичными числами и по тем же основным правилам двоичной арифметики. Однако для того, чтобы результаты сложения и вычитания были также представлены в двоично-десятичном коде, часто требуется вводить специальную коррекцию в коды, полученные после сложения и вычитания.

При суммировании коррекция производится в случае, если значение какой-либо тетрады (четырех двоичных разрядов, кодирующих десятичную цифру) полученного результата будет больше 1001 или, если есть перенос из данной тетрады в более старшую. Наличие такого переноса процессором определяется по состоянию флагов AF и CF. Дело в том, что, используя 4 двоичных разряда, для представления одной десятичной цифры мы, фактически, реализуем шестнадцатеричную систему счисления. Однако, вычислительные операции должны проводиться с числами в двоично-десятичной системе счисления с весами разрядов 8421, в которой 6 кодов тетрады (1010, 1011, 1100, 1101, 1110 и 1111) являются запрещенными, их быть не должно. А поскольку для осуществления операций сложения и вычитания используются обычные двоичные сумматоры, перенос между разрядами происходит как при работе с шестнадцатеричными числами, т.е. после кода 1111 (15₁₀), а не 1001 (10₁₀), как это должно быть при двоично-десятичной системе счисления. Поэтому, для формирования результата в требуемой двоично-десятичной системе, и должна производиться коррекция результата, путем добавления числа 0110 (6₁₀) в те тетрады результата, значение которых больше 1001 или, если из этой тетрады был перенос в более старшую тетраду. (6 = 16 – 10→ разница между основаниями шестнадцатеричной и десятичной систем счисления).

Таким образом, операция суммирования двух двоично-десятичных кодов без знака осуществляется по следующему алгоритму.

- Осуществляется операция суммирования двух исходных двоично-десятичных кодов, рассматривая их как обычные двоичные коды без знака.

- Если результат суммирования в какой-либо тетраде двоичного результата будет > 9, или произойдет перенос из этой тетрады в более старшую (CF=1 или AF=1), то в данной тетраде производится коррекция суммирования.

- Коррекция суммирования заключается в том, что в этих тетрадах к результату суммирования прибавляется 0110.

Примеры:

1. 01000110: (46 + 38 = 84).

+: Состояние флагов: ZF=0; AF=0; PF=1; CF=0.

00111000: Поскольку флаг CF=0; переноса из старшего разряда а, следователь-

------------: но и переполнения разрядной сетки, нет, и результат достоверен.

01111110: Однако значение кода младшей тетрады результата больше 1001.

+: Это означает, что необходимо ввести коррекцию в младшую тетра-

0110: ду, т.е. прибавить к ней 0110.

------------:

10000100:

2. 01001001: (49 + 58 = 107).

+:

01011000: Есть перенос из младшей тетрады в старшую и, кроме того, старшая

--------------: тетрада результата содержит код, больший 1001. Следовательно, и

10100001: в младшую и в старшую тетраду должна быть внесена коррекция.

+: После коррекции происходит перенос из старшего разряда резуль-

01100110: тата, что характеризует переполнение разрядной сетки результата.

---------------: Состояние флагов: ZF=0; AF=1; PF=0; CF=1.

1: 00000111:

3. 01010010: (52 + 34 = 86).

+: Переноса из младшей тетрады в старшую тетраду нет, и обе тетрады

00110100: не превышают значения 1001. Следовательно, коррекция результата

-------------: не требуется. Состояние флагов: ZF=0; AF=0; PF=0; CF=0.

10000110:

Операция вычитания целых двоично-десятичных чисел осуществляется похожим образом, но имеет ту особенность, что при вычитании переполнение разрядной сетки не может произойти принципиально, однако при вычитании уменьшаемое может оказаться меньше вычитаемого. При этом возникает заем из старшего разряда, который фиксируется, аналогично переносу, установкой флага CF в единицу. Это характеризует отрицательный результат и, следовательно, он будет представлен в дополнительном коде, который необходимо преобразовать в прямой код и только после этого корректировать результат. Коррекция, как и в случае сложения, осуществляется либо при значении декады больше 1001, либо при установке флагов CF или AF в единицу и заключается в том, что из соответствующей тетрады результата, вычитается код 0110.

Таким образом, алгоритм вычитания двоично-десятичных целых чисел сводится к следующему.

- Осуществляется операция вычитания двух двоично-десятичных чисел, рассматриваемых как обычные двоичные числа.

- Если результат положительный (уменьшаемое больше вычитаемого), флаг CF=0, то результат анализируется на состояние флага AF и на полученные значения тетрад. Если значение тетрады больше 1001, или флаг, AF=1, то из соответствующей тетрады результата вычитается константа 0110.

- Если результат отрицательный (CF=1), то полученный двоичный код результата является дополнительным, он преобразуется в прямой код, который затем корректируется по тетрадно, т.е., при значении данной тетрады больше 1001, из нее вычитается константа 0110.

Примеры:

1. 10000011: (83 – 61 = 22).

-: ZF=0; AF=0; PF=1; CF=0.

01100001: Переносов из тетрад нет, и обе они меньше 1001.

-------------: Коррекция не требуется.

00100010:

2. 10000001: (81 – 69 = 12).

-: Состояние флагов: ZF=0; AF=1; PF=1; CF=0.

01101001: Поскольку есть заем из старшей тетрады в младшую (AF=1),

-------------: в младшую тетраду результата вводится коррекция.

00011000:

-:

0110:

-------------:

00010010:

3. 00011000: (18 – 87 = − 69).

-: Состояние флагов: ZF= 0; AF=0; PF=0; CF=1.

10000111: Поскольку есть заем в старший разряд (CF=1), то

--------------: результат отрицательный и получен в дополнительном коде.

1: 10010001: Результат в дополнительном коде.

1: 01101111: Результат в прямом коде. Младшая тетрада больше 1001,

-: и, следовательно, производится коррекция младшей тетрады.

0110:

---------------:

1: 01101001: Прямой двоично-десятичный код результата.

Примечание. Введение коррекций при программировании на языке Ассемблера операций сложения и вычитания двоично-десятичных чисел в кодах ASCII, реализуется при подаче команды AAA, после команды операции сложения, и AAS, после команды операции вычитания.

Если же производятся операции сложения или вычитания двоично-десятичных кодов в упакованных форматах, то после команды сложения, для коррекции результата, надо ввести команду DAA, а при вычитании – команду DAS.

Операции сложения и вычитания целых чисел со знаком.

При представлении целых чисел со знаком, старший разряд кода является разрядом знака, в котором положительные числа кодируются 0, а отрицательные – 1. При этом, положительные числа представляются прямым кодом, а отрицательные – дополнительным. Так они хранятся и в оперативной памяти компьютера.

При сложении целых чисел со знаком операция сводится к обычному сложению кодов чисел, включая и знаковый разряд. При осуществлении операции вычитания, код вычитаемого преобразуется в дополнительный код (учитывая и знаковый разряд) и суммируется с кодом уменьшаемого.

Знак результата и в том, и в другом случае определяется автоматически по состоянию знакового разряда. Признак переполнения разрядной сетки результата, в этом случае, определяется функцией неравнозначности переносов в знаковый разряд результата и из его знакового разряда. Если же при осуществлении операции имеются оба этих переноса, или они оба отсутствуют, то переполнения разрядной сетки отсутствует и результат является достоверным.

Для упрощения определения переполнения разрядной сетки сумматора, числа со знаком в современных компьютерах, непосредственно в операционном узле, обрабатываются будучи представленными в модифицированных кодах. Модифицированные коды отличаются от обычных только тем, что для знака числа в них выделяется не один, а два разряда. При этом положительные числа характеризуются значением 00 этих разрядов, а отрицательные – 11.

Если же результат операции будет иметь в знаковых разрядах значения 10 или 01, это будет характеризовать отрицательное (10) или положительное (01) переполнение разрядной сетки и результат должен быть признан недостоверным. Это следует из функции неравнозначности указанных выше переносов.

Приведем примеры арифметических операций с числами, представленными в модифицированных кодах.

Примеры:

1. 111001101: (− 51) + (− 81) = (− 132).

+: Состояние флагов: OF=1; SF=0; ZF=0; AF=1; PF=0; CF=1.

110101111: Переноса в знаковый разряд нет, но перенос из знакового

----------------: разряда есть (знаковые разряды результата 10). Следовательно,

1: 101111100: имеет место отрицательное переполнение разрядной сетки и

: результат недостоверный.

2. 001010101: (+85) + (+ 75) = (+160).

+: Состояние флагов: OF=1; SF=1; ZF=0; AF=1; PF=1; CF=0.

001001011: Перенос в знаковый разряд есть, но переноса из знакового

---------------: разряда нет (знаковые разряды результата 01). Следовательно,

010100000: имеет место положительное переполнение разрядной сетки

: и результат недостоверный.

3. 000010011: (+ 19) + (+79) = (+98).

+: Состояние флагов: OF=0; SF=0; ZF=0; AF=1; PF=0; CF=0.

001001111: Нет переносов ни в знаковый разряд, ни из знакового разряда

--------------: (знаковые разряды результата 00). Следовательно, результат

001100010: достоверный, положительный, в прямом коде.

4. 110011110: (−98) + (−15) = (−113).

+: Состояние флагов: OF=0; SF=1; ZF=0; AF=0; PF=0; CF=1.

111110001: Есть перенос и в знаковый разряд и из знакового разряда:

-----------------: результат достоверный, отрицательный, (знаковые разряды

1: 110001111: результата 11) и представлен в дополнительном коде.

5. 000111011 000111011: (+ 59) − (− 37) = (+ 96).

− → +: Состояние флагов: OF=0; SF=0; ZF=0; AF=1;

111011011 000100101: PF=1; CF=0;

------------- ---------------: Переносов в знаковый и из знакового разряда

001100000: нет (знаковые разряды результата 00):

: результат достоверный, положительный,

: в прямом коде.

6. 110110111 110110111: (− 73) − (+ 69) = (− 142).

− → +: Нет переноса в знаковый разряд, но есть пере-

001000101 110111011: нос из знакового разряда (знаковые разряды

------------ --------------: результата 10): результат недостоверный,

1: 101110010: имеет место отрицательное переполнение

: разрядной сетки.

: Состояние флагов: OF=1; SF=0; ZF=0; AF=1;

: PF=1; CF=1.

При использовании операций сложения и вычитания двоично-десятичных чисел со знаком, алгоритм их проведения остается тем же, однако особенностью этих операций является способ преобразования прямых кодов двоично-десятичных чисел в дополнительные, и дополнительных в прямые. Ниже приведен пример преобразования прямых двоично-десятичных кодов в дополнительные (аналогично производится и преобразование дополнительных двоично-десятичных кодов в прямые).

00110111 - прямой двоично-десятичный код числа 37;

11001001 – дополнительный код исходного двоичного кода;

-

01100110 – вычитание из тетрад константы 0110;

-------------

01100011 – дополнительный код исходного двоично-десятичного

числа: 63.

Операции умножения и деления двоичных целых чисел.

Операции умножения и деления чисел, по сравнению с операциями сложения и вычитания существенно сложнее. Поэтому для них разработано очень много алгоритмов, отличающихся по критериям сложности реализации и быстроты выполнения. Отметим только основные принципы их выполнения. Прежде всего, заметим, что при реализации операций и умножения и деления используются как комбинационные схемы обработки (выполняющие операцию за один тактовый интервал), так и накапливающие схемы обработки (выполняющие операцию за несколько тактовых интервалов). Комбинационные схемы более быстродействующие, но накапливающие более просты.

Принципы умножения чисел сводятся к последовательности операций сложения и сдвига, а принципы деления – к последовательности операций вычитания и сдвига.

Перед осуществлением собственно умножения чисел всегда выполняются две предварительные операции:

1. Анализ сомножителей на равенство 0. При равенстве 0 хотя бы одного из сомножителей, умножение как таковое не производится, а результату (произведению) автоматически присваивается нулевое значение.

2. Если ни один из сомножителей не равен 0, определяется знак произведения, как логическая функции неравнозначности знаковых разрядов сомножителей (S_пр= S₁ 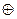S₂).

Перед осуществлением собственно деления чисел всегда выполняются предварительно четыре операции.

1. Анализ делителя и делимого на 0. При делителе = 0, процесс прекращается, и процессор уходит на прерывание, сообщая об этом пользователю. Если равно 0 делимое, процесс также прекращается, и в регистр результата сразу записываются нули.

2. Анализ на необходимость выполнения деления, т.е. выяснение, не меньше ли делимое делителя. Для этого производится предварительная операция вычитание делителя из делимого, выровненных по младшему разряду. Если при этом получается отрицательный результат, то делитель больше делимого и, поскольку в процессоре осуществляется только целочисленное деление, в регистр частного сразу записывается 0. Затем восстанавливается содержимое регистра делимого, путем сложения этого отрицательного результата с содержимым аккумулятора, где хранилось делимое, и это восстановленное значение делимого рассматривается как остаток.

3. Анализ на возможность достоверного деления заданных операндов, так как при слишком малом делителе результат может выйти за пределы разрядной сетки, т.е. произойдет переполнение разрядной сетки результата. Для такого анализа производится предварительная операция вычитания делителя из делимого, выровненных по старшим единичным разрядам. Если при этом получается положительный результат, то частное не войдет в разрядную сетку и процессор уйдет на прерывание.

4. Определяется знак частного, как функции неравнозначности знаковых разрядов делимого и делителя.