Теория множеств

Основной вклад в представление о бесконечности в математике внесён теорией множеств: идея актуальной бесконечности и разных сортов бесконечности занимают существенную часть этой теории.

Для измерения разных видов бесконечности в теории множеств вводится понятие мощности (кардинального числа), совпадающее с количеством элементов для конечных множеств, а для бесконечных множеств задействующее принцип биекции: если между множествами возможно установить взаимно-однозначное соответствие, то они равномощны. Так, оказывается, что множество натуральных чисел 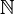равномощно множествам целых чисел (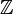), чётных натуральных чисел, всех рациональных чисел (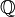), а отрезок числовой прямой (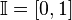, континуум^[⇨]) оказывается в биективном соответствии со всей числовой прямой (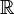), а также с 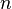-мерным евклидовым пространством (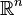). Мощность множества натуральных чисел и равномощных ему (счётных множеств)^[⇨] обозначается 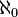, а мощность континуума — . Далее, установлено, что между множеством всех подмножеств натуральных чисел (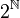) и континуумом есть взаимно-однозначное соответствие, таким образом, 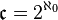, и что счётное множество — наименьшее по мощности из всех бесконечных множеств. Согласно континуум-гипотезе, между 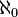и нет промежуточных мощностей (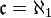), притом, как показал Коэн в 1962 году, ни она, ни её отрицание недоказуемы в основных аксиоматиках теории множеств. Обобщённая континуум-гипотеза предполагает, что все кардинальные числа подчиняются соотношению 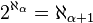, иными словами, все возможные бесконечные кардинальные числа в точности представляют мощности последовательного взятия булеана от множества натуральных чисел: 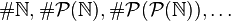^[12].

Представление порядковых чисел до 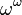: каждый виток спирали — степень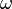

Другой вид бесконечностей, введённый теорией множеств — порядковые числа (ординалы), наряду со связанным с ними принципом трансфинитной индукции они вызвали наибольшие дискуссии в среде математиков, логиков и философов. Если кардинальные числа характеризуют класс эквивалентности относительно взаимно-однозначного соответствия, то порядковое число возникает как характеристика класса эквивалентности над вполне упорядоченными множествами, относительно биективных соответствий, сохраняющих отношение полного порядка. Для конечных множеств ординал и кардинал совпадают, но для бесконечных множеств это не всегда так, все множества одного порядкового числа равномощны, но обратное, в общем случае, неверно. Конструируются ординалы таким образом, чтобы последовательно продолжить натуральный ряд за пределы бесконечности^[13]:

,

,

…

,

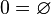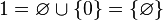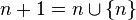после чего, рассмотрев множество всех конечных порядковых чисел как 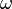, вводится арифметика порядковых чисел^[en] на базе операций сложения упорядоченных множеств (введением порядка над раздельным объединением последовательно по элементам первого слагаемого множества, потом второго) и произведения (над декартовым произведением вполне упорядоченных множеств с использованием лексикографического порядка), и продолжается процесс:

,

,

…

,

,

…

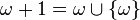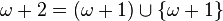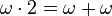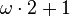Далее строится 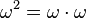, далее — 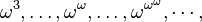, далее — 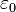-числа^[en]:

.

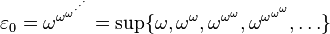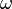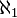Доказано, что множество всех счётных ординалов (всех и ) обладает мощностью — следующей за мощностью счётного множества 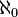, далее строятся ординалы высших порядков. Трансфинитная индукция — обобщение принципа математической индукции, позволяющий доказывать утверждения относительно любого вполне упорядоченного множества с использованием идеи порядковых чисел. Парадокс Бурали-Форти показывает, что множество всех порядковых чисел противоречиво, но во многих аксиоматизациях теории множеств построение такого множества запрещено.

Идейным ядром логического позитивизма (неопозитивизма) стала группа философов и учёных, сформированная и организованная профессором Морицом Шликом при кафедре индуктивных наук Венского университета в 1922 или 1924 году, которая получила название «Венский кружок».

Логический позитивизм ещё часто называют логическим эмпиризмом. Он имеет своим предшественником Дэвида Юма, который отвергал претензии на знание таких метафизических вопросов, как существование Бога и бессмертие души, так как идеи, на которых эти претензии основываются, не могут быть прослежены к простым чувственным впечатлениям, являющимися их источником. Таким же образом члены Венского кружка отвергали как бессмысленные любые утверждения, которые не проверяемы эмпирически. Посредством этого критерия верифицируемости они считали, что метафизические утверждения бессмысленны.

В манифесте Венского кружка было записано: «Если кто-либо утверждает: „Существует Бог“, „Первоначальной причиной мира есть бессознательное“, „Существует энтелехия, которая является основой жизни существ“, то мы не должны говорить: „То, что вы говорите, ошибочно“, а должны скорее спросить: „Что вы имеете в виду под этими предложениями?“ По-видимому, существует четкое разделение между двумя типами утверждений. Один из типов включает утверждения в том виде, как они высказаны в эмпирической науке, их значение может быть определено логическим анализом, или, более точно, сведением к простым предложениям об эмпирически данном. Другие утверждения, включая вышеупомянутые утверждения, оказываются полностью бессмысленными, если мы берем в том смысле, в котором использует их метафизик».^[2]

Можно выделить два исторических корня логического позитивизма. Так в своей программной статье «Поворот в философии» немецко-австрийский философ Мориц Шлик представил генетическую линию развития от Лейбница до Б.Рассела и Г.Фреге. Сама идея «Венского кружка» была инициирована «Principia Mathematica» Рассела и Уайтхеда. Основанием и развитием логики формальных отношений была заложена основа для будущей грандиозной эпистемологической реформы. Став вторым после аристотелевской классической логики силлогизмов инструментом познания, математическая логика послужила материалом строительства здания новой единой науки (своего рода Нового Органона Наук). Успехи, достигнутые в логике, убеждали в силе рациональных процедур мышления, заставляли верить в скорое и неизбежное слияние наук (при доминировании физики, биологии и математики). Отсюда пошло и название — «позитивизм». Задача, поставленная перед «венцами» — разработка системы критериев оценки качества теоретического вывода. Поэтому самое распространенное понимание позитивизма этого времени — это тезис единства метода.

Другое родовое понятие позитивизма — это система языка. Шлик считал, что Л. Витгенштейн был «первым, кто приблизился» к идеям позитивной науки в 1922 году в «Логико-философском трактате» (смотри далее).

Новая методология проводила активный отбор пригодного научного знания и начала с атак на метафизику. „Философия — это не наука“ — утверждал М. Шлик. Требование заменить содержательность как сверхзадачу формальностью стало важным этапом освобождения научного метода от химер и мистификаций обыденного сознания, что напомнило борьбу Бэкона с идолами. В целом 30−40-е годы XX века европейская наука встретила в жарких спорах при общей победе рационализма. Наука, воодушевленная успехами естествознания и объяснявшая этот прорыв совершенством метода, предприняла попытку восстановить единое знание о мире и природе. „Набрав сил, огонь познания охватывает и остальное. Эти моменты свершения и горения — самое существенное. Весь свет познания идет от них. Поисками источника этого света философ на самом деле и занят, когда он ищет последний фундамент познания“^[3].