Доказательство. Запишем интегральную сумму функции для данного разбиения отрезка и данного выбора точек : где и - интегральные суммы функций y = f(x) и y = g(x) для

Запишем интегральную сумму функции 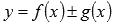для данного разбиения отрезка и данного выбора точек :

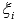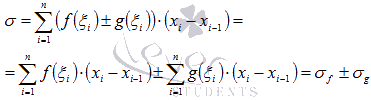
где 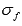и - интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.

Переходя к пределу при 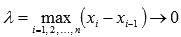получим 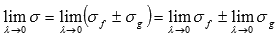, что по определению интеграла Римана равносильно утверждению доказываемого свойства.

4. Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке [a; b] функции y = f(x) и произвольного числа k справедливо равенство .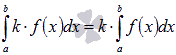

Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:

5. Пусть функция y = f(x) интегрируема на интервале X, причем 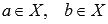и 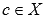, тогда .

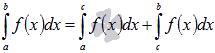Это свойство справедливо как для 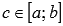, так и для 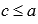или .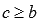

Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.

6. Если функция интегрируема на отрезке [a; b], то она интегрируема и на любом внутреннем отрезке .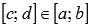

Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.

7. Если функция y = f(x) интегрируема на отрезке [a; b] и 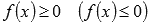для любого значения аргумента 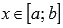, то .

Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек 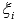при 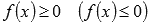будет неотрицательной (не положительной).

Date: 2015-06-08; view: 587; Нарушение авторских прав