
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Постулирование базовой таблицы форм
|
|
Данный раздел вызовет наибольшее раздражение у гуманитариев и, напротив, принесет некоторое отдохновение души технократам, скептически воспринимающим "философские рассуждения". Остается лишь призвать первых потерпеть, а вторых – не обольщаться.
Автор, безусловно, относится к нормальному большинству людей, которое на дух не переносит никаких "формул". Но появляющиеся ниже в тексте непривычные значки, строго говоря, не являются формулами. Это просто обозначения клеток "таблицы" вроде значков шахматной нотации ("ферзь стоит на поле h7") или географических координат (широты и долготы). Разобраться в этих обозначениях без труда может любой гражданин, имеющий восемь классов за плечами. Никакого знания математики не предполагается. Короче: если у вас при чтении возникают трудности – дело не в "формулах" и не в "математике". Исходите из того, что вы знаете заведомо больше, чем требуется для понимания.
Приступаем к построению базовой "таблицы" форм.
1. Изобразим на плоскости квадратную таблицу 3х3 для игры в "крестики - нолики", состоящую из девяти клеток. Обозначим нижнюю левую клетку символом @, среднюю – символом & и верхнюю правую – символом *.
2. Обозначим строки таблицы снизу вверх символами K{@}, K{&}, K{*}. Обозначим столбцы таблицы слева направо символами F{@}, F{&}, F{*}.
3. Теперь пририсуем вплотную к этой таблице еще восемь точно таких же: по одной справа и слева, по одной сверху и снизу и еще четыре – по диагоналям. В каждой из этих таблиц обозначим три диагональные клетки теми же символами и в том же порядке: @, &, *.
4. Теперь представим себе, что это "пририсовывание" распространяется и дальше во все стороны по принципу цепной реакции и дает в пределе бесконечную плоскость, покрытую сплошным "ковром" девятиэлементных таблиц со все той же тройкой непонятных символов на диагонали.
5. Очевидно (легко проверить на картинке), что каждая из тех пока пустых клеток этой бесконечной таблицы, в которой нет ни одного из трех символов @,&,*, всегда граничит ровно с двумя клетками, содержащими различные два из этих трех символов; причем одна из таких содержащих символы клеток содержится в том же столбце (рядом сверху или рядом снизу), а другая – в той же строке (рядом слева или рядом справа). С учетом этого обстоятельства, присвоим составной символ каждой из остающихся пустыми клеток по следующему правилу.
Если ближайшая справа от нее клетка содержит один из трех диагональных символов, например, &, то первая часть составного символа будет иметь вид K{&}n (где n – верхний индекс); если ближайшая слева от нее клетка содержит один из трех диагональных символов, например, @, то первая часть составного символа будет иметь вид K{@}r (где r – нижний индекс). Далее, если ближайшая снизу от нее клетка содержит один из трех диагональных символов, например, @, то вторая часть составного символа будет иметь вид F{@}t (где t – верхний индекс); если ближайшая сверху от нее клетка содержит один из трех диагональных символов, например, &, то вторая часть составного символа будет иметь вид F{&}i (где i – нижний индекс).
Легко убедиться, что какой бы квадрат из девяти клеток не вырезать из нашего ковра, на нем всегда окажется тем или иным способом размещен стандартный набор из девяти символов – трех диагональных (простых) и шести составных для остальных шести клеток:
@, &, *, K{*}rF{@}i, K{*}nF{&}t, K{&}rF{*}i, K{&}nF{@}t, K{@}rF{&}i, K{@}nF{*}t.
6. Теперь осталось осуществить единственную нетривиальную операцию, которая не вызовет затруднений у математиков, привыкших иметь дело с многомерными пространствами. "Свернем" нашу таблицу таким образом, чтобы все клетки, обозначенные одним и тем же символом, совместились друг с другом; таким образом, мы получим некий многомерный глобус, чья поверхность будет разбита ровно на девять ячеек, содержащих указанные выше три простых и шесть составных символов. Неискушенным читателям, которые сомневаются в осуществимости подобной операции, можно объяснить этот фокус менее строго, но более наглядно: нужно просто взять нашу исходную квадратную таблицу 3х3 и свернуть ее вокруг четырех осей: горизонтальной, так чтобы нижний край склеился с верхним и получилась горизонтальная трубочка-цилиндр; вертикальной, так чтобы левый край склеился с правым и получилась вертикальная трубочка-цилиндр; диагональной, так чтобы левый нижний угол склеился с правым верхним; другой диагональной, так чтобы левый верхний угол совпал с правым нижним. Вся проблема лишь в том, что эти четыре склейки нужно осуществить одновременно... Очевидно, пространство, в котором возможны такие операции, должно иметь более трех измерений. В дальнейшем описанное свойство базовой "таблицы" форм будем называть свойством четырехмерной свертки.
| K{@}rF{&}i | K{@}nF{*}t | @ |
| K{*}nF{&}t | * | K{*}rF{@}i |
| & | K{&}rF{*}i | K{&}nF{@}t |
По-видимому, можно показать, что вся "таблица" в целом будет представлять собой спиралошар [18], многомерный аналог листа Мебиуса, своими парадоксальными свойствами напоминающий "Бытие" элейцев – шаровую вселенную, одновременно открытую и замкнутую, конечную и бесконечную. Но к этим свойствам лучше вернуться позднее, уже на уровне космологической интерпретации.
7. Наконец, мы можем вернуться к элементарной двумерной проекции базовой "таблицы" форм, с которой по большей части и будем в дальнейшем иметь дело. Теперь каждая из девяти клеток однозначным образом получила собственный символ. Результат может выглядеть следующим образом:
| K{*}r F{@}i K{*}n F{&}t * |
| K{&}n F{@}t & K{&}rF{*}i |
| @ K{@}r F{&}i K{@}n F{*}t |
Следует только помнить, что базовая "таблица" имеет девять совершенно равноправных плоских квадратных проекций, и вышеприведенная выбрана из них по соображениям интерпретации, которые станут ясны в дальнейшем. Приведем для примера еще три из оставшихся восьми проекций:
| K{&}rF{*}i K{&}nF{@}t & |
| K{@}nF{*}t @ K{@}rF{&}i |
| * K{*}rF{@}i K{*}nF{&}t |
| @ K{@}rF{&}i K{@}nF{*}t |
| K{*}rF{@}i K{*}nF{&}t * |
| K{&}nF{@}t & K{&}rF{*}i |
Полезно также все время помнить, что в каждой из таких таблиц-проекций любой столбец, любая строка и любая из двух диагональных осей являются на самом деле замкнутыми "кольцами" из трех элементов.
Интерпретация базовой "таблицы" форм. Отношения "восхождения" и "нисхождения". "Номинальное" и "реальное". "Имманентное" и "трансцендентное".
Интерпретация базовой "таблицы" форм состоит в том, что символы, обозначающие элементы "таблицы" и отношения между ними, отождествляются с такими терминами, которые, при их употреблении в общекультурном или специальном контексте, приобретают известное общечеловеческое или профессиональное содержание. Само это содержание, однако, на данном этапе не рассматривается и не уточняется. Таким образом, интерпретация базовой "таблицы" имеет характер намека, указания на определенное содержание. Однако это не просто формальное сопоставление. При конкретизации указанного содержания "таблица" должна давать возможность (с той мерой адекватности, с какой она воспроизводит структуру универсума форм) сопоставить более конкретным общекультурным и специальным терминам соответствующие более конкретные элементы и отношения "таблицы".
Итак, переходим к интерпретации базовой "таблицы" форм. Начнем с наиболее абстрактных интерпретаций составных символов и отношений, не зависящих от интерпретации конкретных диагональных символов чистых форм.
Если "форма А" есть интерпретация диагонального символа "s", то:
K{s} интерпретируется как категория А;
F{s} интерпретируется как формация А.
Если "d" и "g" – символы чистых форм, "форма D" есть интерпретация диагонального символа "d", а "форма G" есть интерпретация диагонального символа "g", и клетка "g" расположена на диагонали "таблицы" непосредственно вслед за клеткой "d", правее и выше ее, то:
– "форма G" интерпретируется как "восходящая" по отношению к "форме D", а "форма D" – как "нисходящая" по отношению к "форме G";
– переход от клетки "d" к клетке "g" интерпретируется как "восхождение", а обратный переход – как "нисхождение";
– категория K{g} интерпретируется как "более конкретная" по отношению к категории K{d}, а категория K{d} – как "более абстрактная" по отношению к категории K{g};
– формация F{g} интерпретируется как "более сложная" по отношению к формации F{d}, а формация F{d} – как "более простая" по отношению к формации F{g}.
Если "форма А" есть интерпретация диагонального символа "s", то:
K{s}r интерпретируется как реальная форма категории А;
K{s}n интерпретируется как номинальная форма категории А;
F{s}i интерпретируется как имманентная форма формации А;
F{s}t интерпретируется как трансцендентная форма формации А.
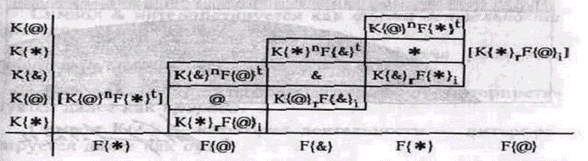 Последнюю интерпретацию сопроводим более наглядной графической параллелью. Для этого рассмотрим еще одну плоскую проекцию "таблицы" форм специального вида.
Последнюю интерпретацию сопроводим более наглядной графической параллелью. Для этого рассмотрим еще одну плоскую проекцию "таблицы" форм специального вида.
Здесь в левом столбце обозначены категории, а в нижней строке – формации. Для удобства составные формы K{*}rF{@}i и K{@}nF{*}t показаны на проекции дважды, хотя это пары проекций одной и той же "клетки-ячейки" "таблицы" форм ("вторые" экземпляры этих форм в таблице заключены в квадратные скобки). Благодаря этому каждый из трех простых символов оказался в окружении четырех составных. Из данной таблицы легко видеть, что все формы, обозначенные символами с верхними индексами (в интерпретации – "номинальные" и "трансцендентные") располагаются соответственно левее и выше диагональных (чистых) форм, а все формы, обозначенные символами с нижними индексами (в интерпретации – "реальные" и "имманентные") располагаются соответственно правее и ниже диагональных (чистых) форм.
Date: 2015-06-07; view: 616; Нарушение авторских прав