Основные теоретические положения. Маятником называют твердое тело, которое совершает колебания относительно неподвижной точки или оси под действием силы тяжести

Маятником называют твердое тело, которое совершает колебания относительно неподвижной точки или оси под действием силы тяжести. Различают:

Математический маятник, под которым понимают материальную точку массой т, подвешенную на длинной невесомой и нерастяжимой нити. Эта материальная точка совершает малые колебания в вертикальной плоскости под действием силы тяжести.

Физический маятник, под которым понимают тело массой т, колеблющееся относительно горизонтальной оси О, не проходящей через центр инерции.

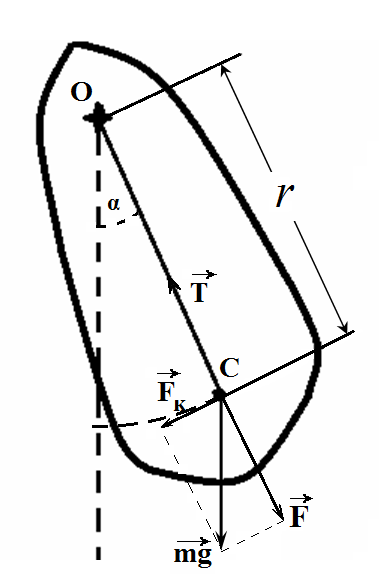Получим уравнение движения фи­зического маятника. Для этого применим уравнение динамики вращательного дви­жения, так как траектория движения центра инерции маятника – элемент окружности.

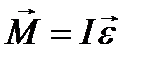, (1)

где 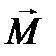- механический момент силы тяжести 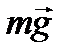; I - момент инерции маятника относительно т.О; ε - угловое ускорение, численно равное второй производной углового перемещения α по времени ().

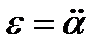Момент силы тяжести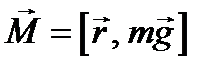

или в скалярной форме ,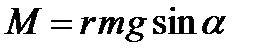

где 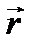– радиус-вектор центра инерции относительно т.О, g – ускорение свободного падения, α – угол между 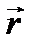и 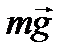численно равный угловому перемещению центра инерции. В итоге уравнение (1) имеет вид

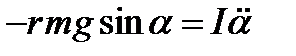. (2)

Знак «минус» указывает на то, что момент силы направлен в противо­по­ложную сторону углового перемещения α.

Преобразуем уравнение (2). Получили нелинейное дифференци­альное уравнение 2-го порядка

,

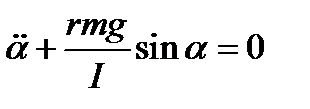решением которого будет ангармоническая функция α(t), период кото­рой зависит от полной энергии маятника.

Если же угол 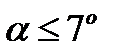, 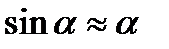и данное уравнение принимает вид 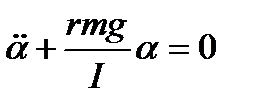. Решение этого уравнения будет гармонической функцией 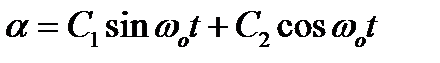, где 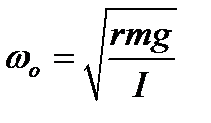– круговая или циклическая частота. Параметры С₁ и С₂ – определяются из на­чальных и граничных условий колебаний и являются амплитудой колебаний. Круговая частота связана с периодом колебания Т уравнением

.

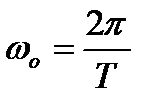Тогда период колеба­ния физического маятника равен

. (3)

Для математического маятника, масса которого сосредото­чена в материальной точке, подвешенной на нити длиной l, момент инерции

.

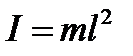Тогда период мате­матического маятника

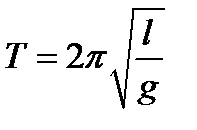. (4)

Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маят­ника.

Из сравнения формул (3) и (4) определяем приведенную длину как

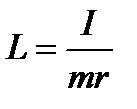. (5)

Таким образом, период колебания физического маятника равен

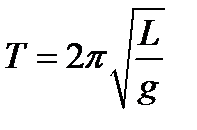. (6)

Date: 2015-05-04; view: 525; Нарушение авторских прав