Практическая работа № 3

Теоретическая часть:

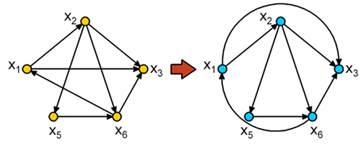
	Граф G =(V, E), который может быть изображен на плоскости или сфере без пересечений называется планарным
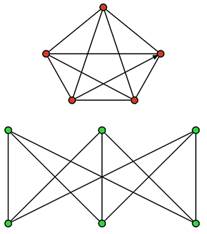
	На рисунке показаны непланарные графы. Эти два графа играют важную роль в теории планарных графов и известны как графы Куратовского.

Неориентированный граф G = (V, E) называют двудольным, если множество его вершин V может быть разбито на такие два подмножества V^а и V^b, что каждое ребро имеет один конец в V^а, а другой в V^b (рисунок 1,а).

Ориентированный граф G называется двудольным, если его неориентированный двойник – двудольный граф (рисунок 1,б,в).

Двудольный граф G=(V^а∪V^b, E) называют полным, если для любых двух вершин v_i∈V^а и v_j ∈V^b существует ребро (v_i,v_j) в G=(V,E) (рисунок 1,г).

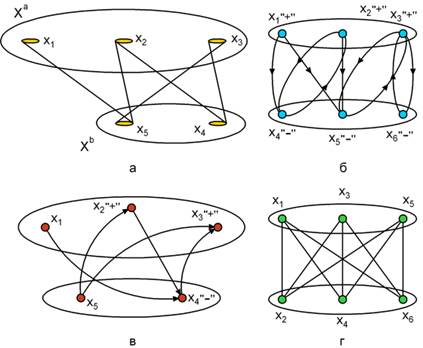
Рисунок 1

Теорема (X. Уитни, 1932 г.). Граф планарен тогда и только тогда когда он имеет абстрактно двой­ственный граф.

Говорят, что граф G укладывается на поверхности S, если его можно нарисовать на этой поверхности так, что его ребра будут пересекаться лишь в концевых точках - вершинах. Граф называется планарным, если его можно уложить на плоскости. Изображение планарного графа на плоскости называют планарной укладкой. Для каждого простого планарного графа существует планарная укладка, в которой все ребра графа будут прямыми линиями.

Если граф не укладывается на плоскости (поверхности нулевого порядка), то его можно уложить на какой - либо другой поверхности (более высокого порядка). Укладываемость графа на плоскости равносильна его укладываемости на сфере, поскольку сфера и плоскость относятся к поверхности нулевого порядка, что можно установить стереографической проекцией сферы на плоскость.

На рисунок 2, а и б показаны две планарные укладки одного и того же графа, а на рисунке в и г приведены два основных непланарных графа – K ₅ и K _3,3 (графы Куратовского).

Графы Куратовского считаются основными непланарнами графами потому, что играют решающую роль в исследовании планарности графов.

Теорема Граф планарен тогда и только тогда, когда каждый его блок планарен.

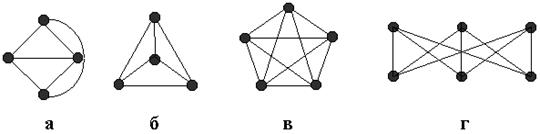
Рисунок 2. Примеры планарного и непланарных графов:
а - планарная укладка с непрямолинейными ребрами;
б - планарная укладка того же графа с прямолинейными ребрами;
в - непланарный граф K ₅; г - непланарный граф K _3,3

До появления статьи Куратовского, в которой был дан критерий планарности графов, характеризация планарных графов была труднейшей нерешенной проблемой. Доказательство приводимой ниже теоремы Куратовского можно найти в книге.

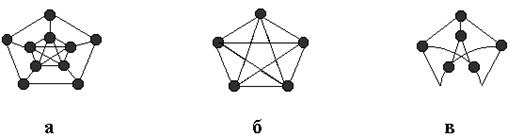
Рисунок 3. Непланарность графа Петерсена: а - граф Петерсена;
б - граф Петерсена, стянутый к K ₅;
в - один из подграфов графа Петерсена, гомеоморфный K _3,3

Граф Петерсена не имеет подграфов, гомеоморфных K ₅, но легко стягивается к K ₅. Сложнее увидеть, что граф Петерсена имеет подграф, гомеоморфный K _3,3.

Уитни связал планарность графов с существованием двойственных графов. Граф G* называется двойственным к графу G, если существует такое взаимнооднозначное соответствие их ребер, что множество ребер графа G* образует цикл тогда и только тогда, когда в графе G это же множество ребер образует разрезающее множество. Для плоского графа существует простой способ построения двойственного графа (см. пример на рисунок 4).

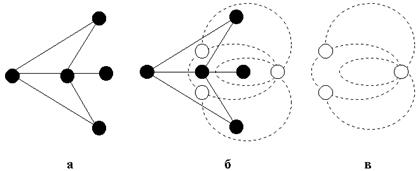
Рисунок 4. Пример: а – граф G; б – построение двойственного графа G*;
в – граф G*, двойственный графу G

Суть способа построения в следующем: а) в каждой области укладки графа G на плоскости размещается вершина графа G*; б) через каждое ребро e графа G, общее для областей 0 _i и 0 _j, проводится линия, соединяющая вершины 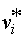и и образующая ребро e*.