
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Корреляционное поле сильной линейной обратной связи
|
|
В случае линейной зависимости у от х уравнением регрессии является уравнение прямой у = а + bх, где у — значение результативного признака (зависимая переменная), х — значения факторного признака (независимая переменная), а и b — коэффициенты
Простейшим примером линейного уравнения регрессии может служить индекс Брока, который используется как росто-весовой индекс для исчисления нормального веса: из роста вычитают 100 и получают нормальный вес, соответствующий этому росту. Математически этот индекс записывается в виде уже приводившегося уравнения линейной регрессии у=а+bх, где у — вес, х — рост, а=–100, b — поправочный коэффициент, который изменяется для разных возрастных групп.
Иногда при измерении расстояний на местности прибегают к счету шагами. Длина шага человека описывается уравнением регрессии L=37 + h/4, где h — рост человека в см, L — длина его шага.
Полная оценка взаимосвязи признаков требует нахождения уравнения регрессии не только для зависимости у от х, но и для зависимости х от у. В силу вероятностного характера статистических взаимосвязей результаты вычислений по этим уравнениям не будут зеркально похожими. Поскольку методика и порядок вычислений в обоих случаях во многом аналогичны, ограничимся рассмотрением основ обработки уравнения у = а + bх (зависимость у от х).
В уравнении у = а + bх коэффициент b равен тангенсу угла наклона линии регрессии. Этот коэффициент, называемый «коэффициент регрессии», имеет большой статистический смысл. Он показывает, насколько изменяется значение одной величины (зависимой, результативной переменной) при изменении второй (независимой, факторной) на единицу. Например: при увеличении температуры тела человека на 1°С, частота пульса увеличивается в среднем на 10 ударов в минуту.
Статистический анализ подразумевает решение уравнения регрессии, т. е. отыскание параметров этого уравнения на основе исходных данных. Математически решение уравнения линейной регрессии сводится к вычислению параметров а и b таким образом, чтобы точки исходных данных корреляционного поля как можно ближе лежали к прямой регрессии. Для этого вычисляют параметры по формулам, которые обеспечивают наименьший квадрат отклонений этих точек от линии регрессии (метод наименьших квадратов):
 и
и 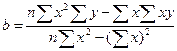
Пример: Найти выборочное уравнение регрессии по данным пяти наблюдений (л=5) зависимой и независимой переменных У и Х.
| Расчетная таблица параметров уравнения регрессии | ||||||||
| i | Xi | Yi | Xi2 | XiYi | ||||
| 2,0 | 2,6 | 4,0 | 5,2 | |||||
| 4,0 | 1,8 | 16,0 | 7,2 | |||||
| 7,0 | 1,3 | 49,0 | 9,1 | |||||
| 5,0 | 1.1 | 25,0 | 5,5 | |||||
| 3,0 | 2,4 | 9,0 | 7,2 | |||||
| X | 21,0 | 9,2 | 103,0 | 34,2 |
Согласно уравнению параметр 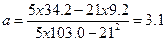
параметр 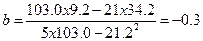
Искомое уравнение регрессии y=3.1+(–0.3)х. Коэффициент регрессии, соответственно, равен –0,3. Т. е. при изменении независимой переменной (х) на 1, зависимая переменная (у) будет уменьшаться в среднем на 0,3.
Насколько близки расчетные и фактические данные по зависимому фактору у, демонстрирует таблица, где Ypac первого наблюдения (i=1) Y1=3,1+(–0,3)х2,0=2,5 и т. д. Нетрудно заметить, что между фактическими и расчетными значениями (Ypac и Yi) существует определенная разница. Эта разница может объясняться малым числом наблюдений и точностью самого метода.
Разность фактического (Yi)и вычисленного (Ypac) параметров
| i | Xi | Yi | Ypac | Yi – Ypac |
| 2.0 | 2.6 | 2.5 | 0.1 | |
| 4.0 | 1.8 | 1.9 | –0.1 | |
| 7.0 | 1.3 | 1.0 | 0.3 | |
| 5.0 | 1.1 | 1.6 | –0.5 | |
| 3.0 | 2.4 | 2.2 | 0.2 |
Параметры уравнения регрессии, как и любые выборочные статистические характеристики, оцениваются в определенных интервалах. В том случае, если уравнение регрессии имеет вид у=а+bх, выборочные значения коэффициентов а и b являются оценкой соответствующих генеральных коэффициентов и отличаются от них в среднем на величину соответствующих им ошибок. Ошибка коэффициента
 , где σх — среднеквадратическое (стандартное) отклонение по ряду х, n — число наблюдений.
, где σх — среднеквадратическое (стандартное) отклонение по ряду х, n — число наблюдений.
Ошибка коэффициента b характеризует разброс значений угла наклона линии регрессии. Полная ошибка для результатов отдельных измерений у:
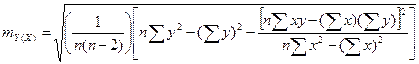
Рассмотренный пример касается так называемой двухмерной зависимости. В этом случае рассматривается вариант, при котором взаимодействуют два признака — зависимый (результативный) и независимый (факторный). В реальной ситуации чаще приходится сталкиваться с многофакторными зависимостями. Соответственно, если рассматривается большее число независимых признаков, то расчеты проводятся по другим формулам, с учетом трехмерного, четырехмерного и т. п. пространства распределения. С математической точки зрения, число пространственных распределений, в принципе, не ограничено.
Обязательным условием такого подхода является независящее друг от друга распределение факторных признаков.
В общем виде формула для расчета коэффициента множественной регрессии для результативного показателя:
Y=β0+ β1X1+ β2X2+…+βnXn,
где β0, β1, β2… βn — коэффициенты регрессии. Например: должные (стандартные) величины показателей ЖЕЛ — жизненной емкости легких вычисляются для мужчин в возрасте 18-25 лет по уравнению регрессии Y=β0+ β1X1+ β2X2 где β0 — константа, равная – 6,908, β1 — коэффициент по росту, равный 5,8, β2 — коэффициент по возрасту 0,085. С помощью этого уравнения, опираясь на фактические данные о конкретном человеке, путем несложных вычислений можно определить должную (стандартную) величину ЖЕЛ этого человека. Так, для мужчины в возрасте 19 лет, имеющему рост 1,8 метра, должная ЖЕЛ = –6,908 + 5,8 х 1,8 + 0,085 х 19 = 5,2. С точки зрения клинической практики, снижение фактической ЖЕЛ по сравнению с должной ЖЕЛ может говорить о рестриктивных нарушениях вентиляционной способности легких, являющихся следствием нарушения процесса расправления легких при вдохе.
Относительная простота применения уравнений регрессии обеспечила их большое распространение: для нахождения должных величин при оценке различных физиологических параметров, в гигиенических исследованиях для прогнозирования результатов воздействия различных факторов окружающей среды и т. п. Вместе с тем, получение точных исходных параметров уравнений регрессии требует большой и кропотливой работы.
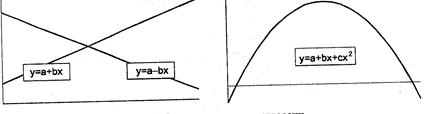
Одной из причин, снижающих точность параметров уравнения регрессии, является несоответствие теоретического распределения, взятого за основу расчетов, и фактического распределения точек корреляционного поля. Например, линия регрессии может представлять собой не прямую, а какую-либо кривую. Соответственно, форма уравнения регрессии должна соответствовать криволинейной зависимости.
Date: 2015-06-06; view: 617; Нарушение авторских прав