
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Критерии, характеризующие внутреннюю структуру совокупности
|
|
Наиболее полную характеристику разнообразию признака в совокупности дает среднее квадратическое отклонение, обозначаемое греческой буквой σ (сигма малая).
5.3.2.1 Расчет среднеквадратического отклонения
Среднее квадратическое отклонение характеризует среднее отклонение всех вариант вариационного ряда от средней арифметической величины.
Существует три способа расчета среднего квадратического отклонения: среднеарифметический, способом моментов и по амплитуде.
Возвратимся к нашему примеру. При среднеарифметическом способе расчета применяется формула:
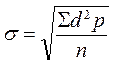
d — отклонение отдельных вариант от средней арифметической (V–M)
р — частота
n — число наблюдений (при числе наблюдений менее 30, в знаменатель необходимо взять n–1).
Порядок вычисления среднего квадратического отклонения представлен в таблице.
Расчет среднего квадратического отклонения
среднеарифметическим методом
| Частота пульса V | Р | d (V – М) М = 72,3 | d2 | d2p | ||||
| – 12,3 | 151,29 | 151,29 | ||||||
| – 10,3 | 106,09 | 212,18 | ||||||
| – 8,3 | 68,89 | 206,67 | ||||||
| – 6,3 | 39,69 | 119,07 | ||||||
| – 4,3 | 18,49 | 55,47 | ||||||
| – 2,3 | 5,29 | 47,61 | ||||||
| – 0,3 | 0,09 | 0,54 | ||||||
| 1,7 | 2,89 | 20,23 | ||||||
| 3,7 | 13,69 | 150,59 | ||||||
| 5,7 | 32,49 | 162,45 | ||||||
| 7,7 | 59,29 | 237,16 | ||||||
| n=54 | Σ 1363,26 | |||||||
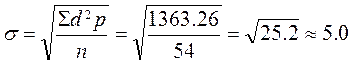
Среднее квадратическое отклонение, также как и среднюю арифметическую, можно рассчитать более простым способом, а именно способом моментов по формуле:
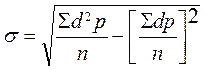 , где
, где
d – отклонение каждой варианты от условной средней (V–А).
Порядок вычисления среднего квадратического отклонения представлен в таблице (за условную среднюю принимаем Мо = 76 ударам в минуту).
| частота пульса V | D(V–A) А=76 | d | dp | d2 | d2p |
| – 16 | – 16 | ||||
| – 14 | – 28 | ||||
| – 12 | – 36 | ||||
| – 10 | – 30 | ||||
| – 8 | – 24 | ||||
| – 6 | – 54 | ||||
| – 4 | – 24 | ||||
| – 2 | – 14 | ||||
| N = 54 | Σ = –200 | Σ = 2104 |
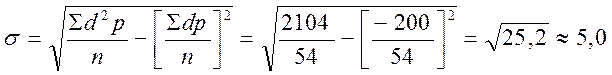
Результаты вычисления среднего квадратического отклонения среднеарифметическим способом и способом моментов идентичны. Однако, как указывалось выше, второй способ значительно убыстряет и упрощает расчеты. Если отсутствуют необходимые исходные данные для вычисления среднего квадратического отклонения обычным путем, может быть использован приближенный способ вычисления среднего квадратического отклонения по амплитуде вариационного ряда.
Среднее квадратическое отклонение, вычисленное по амплитуде, несколько отличается по величине от σ, вычисленной обычными способами. Различие это тем больше, чем больше число наблюдений, использованных для составления вариационного ряда. Поэтому определение среднего квадратического отклонения по амплитуде более целесообразно производить преимущественно при ориентировочных расчетах.
Вычисление производится по формуле:
| σ = | Am | = | Vmax–Vmin |
| k | k |
Am — амплитуда
k — коэффициент, соответствующий числу наблюдений (определяется по специальной таблице, в нашем примере при n=54 коэффициент равен 4,56)
| σ = | 80–60 | = | ≈ 4,4 | |
| 4,56 | 4,56 |
Значения и для вычисления среднего квадратического
отклонения (σ) по амплитуде
| n | ||||||||||
| – | – | 1,13 | 1,69 | 2,06 | 2,33 | 2,53 | 2,70 | 2,85 | 2,97 | |
| 3,08 | 3,17 | 3,26 | 3,34 | 3,41 | 3,47 | 3,53 | 3,59 | 3,64 | 3,69 | |
| 3,73 | 3,78 | 3,82 | 3,86 | 3,90 | 3,93 | 3,96 | 4,00 | 4,03 | 4,06 | |
| 4,09 | 4,11 | 4,14 | 4,16 | 4,19 | 4,21 | 4,24 | 4,26 | 4,28 | 4,30 | |
| 4,32 | 4,34 | 4,36 | 4,38 | 4,40 | 4,42 | 4,43 | 4,45 | 4,47 | 4,48 | |
| 4,50 | 4,51 | 4,53 | 4,54 | 4,56 | 4,57 | 4,59 | 4,60 | 4,61 | 4,63 | |
| 4,64 | 4,65 | 4,66 | 4,68 | 4,69 | 4,70 | 4,71 | 4,72 | 4,73 | 4,74 | |
| 4,75 | 4,77 | 4,78 | 4,79 | 4,80 | 4,81 | 4,82 | 4,83 | 4,83 | 4,84 | |
| 4,85 | 4,86 | 4,87 | 4,88 | 4,89 | 4,90 | 4,91 | 4,91 | 4,92 | 4,93 | |
| 4,94 | 4,95 | 4,96 | 4,96 | 4,97 | 4,98 | 4,99 | 4,99 | 5,00 | 5,01 | |
| n | ||||||||||
| k | 5,02 | 5,49 | 5,76 | 5,94 | 6,07 | 6,18 | 6,28 | 6,35 | 6,42 | 6,48 |
Среднее квадратическое отклонение вычисленное обычными способами дает точную величину (σ = 5,0). Однако различие это не слишком велико и, если бы были известны только крайние варианты ряда, приближенное вычисление среднего квадратического отклонения по амплитуде вариационного ряда имело бы смысл.
Итак, нахождение среднего квадратического отклонения позволяет судить о характере однородности исследуемой группы наблюдений. Если величина среднего квадратического отклонения небольшая, то это свидетельствует о достаточно высокой однородности изучаемого явления.
Среднюю арифметическую в таком случае следует признать вполне характерной, типичной для данного вариационного ряда. При очень большой величине сигмы средняя арифметическая в меньшей степени характеризует весь вариационный ряд, что говорит о значительной вариабельности изучаемого признака или явления или о неоднородности исследуемой группы.
5.3.2.2 Расчет коэффициента вариации
Оценка степени рассеяния вариант около средней может быть произведена с помощью коэффициента вариации, вычисляемого по формуле:
| CV= | σ | x 100% |
| M |
Значения коэффициента вариации (CV)
- менее 10% свидетельствует о малом рассеянии
- от 10% до 20% — о среднем
- более 20% — о сильном рассеянии вариант вокруг средней арифметической
Возвращаясь к нашему примеру мы можем дать характеристику изучаемому вариационному ряду. М=72,3 удара в минуту, σ =5,0
| CV= | 5,0 | x 100% | = 6,9% |
| 72,3 |
Расчеты свидетельствуют о малом рассеянии вариант, следовательно средняя арифметическая величина вполне типична, а исследуемая группа наблюдений является достаточно однородной.
Коэффициент вариации часто используется при оценке разнообразия ряда различных признаков, например, рост и масса тела, средняя длительность лечения на дому и частота врачебных посещений. Непосредственное сравнение «σ» в данном случае невозможно, так как величина среднего квадратического отклонения обычно характеризует рассеянность ряда при сравнении однотипных рядов.
Предположим, что при изучении физического развития группы подростков коэффициент изменчивости для массы тела составил 9%, а для роста — 3,7%. Эти цифры можно сравнивать и сделать заключение, что в данном примере рост является более устойчивым признаком, чем масса тела.
Контрольные вопросы
1. Дайте определение средней величины
2. Какие требования предъявляются при работе со средними величинами?
3. Дайте определение вариационного ряда
4. Назовите основные элементы вариационного ряда
5. Виды вариационных рядов
6. Правила построения вариационного сгруппированного ряда
7. Как определяется средняя арифметическая простая?
8. Как определяется средняя арифметическая взвешенная?
9. Определение средней арифметической способом моментов
10. Назовите критерии разнообразия признака вариационного ряда
11. Что такое среднее квадратическое отклонение и его значение?
12. Роль коэффициента вариации и его применение?
Date: 2015-06-06; view: 735; Нарушение авторских прав