
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Виды средних величин, методика их вычисления
|
|

Различают три вида средних величин: мода (Мо), медиана (Me), средняя арифметическая (М). Они не могут подменить друг друга и лишь в совокупности достаточно полно и в сжатой форме представляют собой особенности вариационного ряда.
Мода (Мо) — наиболее часто встречающаяся в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда. Используется:
- для определения центра распределения в открытых вариационных рядах
- для определения среднего уровня в рядах с резко асимметричным распределением
Медиана — это серединная варианта, центральный член ранжированного ряда. Название медиана взято из геометрии, где так именуется линия, делящая сторону треугольника на две равные части.
Медиана применяется:
- для определения среднего уровня признака в числовых рядах с неравными интервалами в группах
- для определения среднего уровня признака, когда исход-ные данные представлены в виде качественных признаков и когда единственным способом указать некий центр тяжести совокупности является указание варианты (группы вариант), которая занимает центральное положение
- при вычислении некоторых демографических показателей (средней продолжительности предстоящей жизни)
- при определении наиболее рационального места расположения учреждений здравоохранения, коммунальных учреждений и т. п. (имеется в виду учет оптимальной удаленности учреждений от всех объектов обслуживания)
В настоящее время очень распространены различные опросы ((маркетинговые, социологические и др.), в которых опрашиваемых просят выставить баллы изделиям, политикам и т. п. Затем из полученных оценок рассчитывают средние баллы и рассматривают их как интегральные оценки, выставленные коллективом опрошенных. При этом обычно для определения средних показателей применяют среднее арифметическое. Однако такой способ на самом деле применять нельзя. Обоснованным в этом случае является использование в качестве средних баллов медианы или моды.
Для характеристики среднего уровня признака наиболее часто используется в медицине средняя арифметическая величина (М).
Средняя арифметическая величина — это общая количественная характеристика определенного признака изучаемых явлений, составляющих качественно однородную статистическую совокупность. Различают среднюю арифметическую простую и взвешенную.
Средняя арифметическая простая вычисляется для не сгруппированного вариационного ряда путем суммирования всех вариант и делением этой суммы на общее количество вариант, входящих в вариационный ряд.
Вычисляется средняя арифметическая простая по формуле:
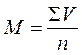
М — средняя арифметическая простая,
ΣV — сумма вариант,
n — число наблюдений
Средняя арифметическая взвешенная вычисляется для сгруппированного вариационного ряда по формуле:
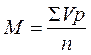
где
М — средняя арифметическая взвешенная,
ΣVp — сумма произведений вариант на их частоты,
n — число наблюдений.
Возвращаясь к нашему примеру, определим среднюю частоту пульса (среднее число ударов в минуту) у 54 студентов перед экзаменом.
| M = | 60х1+62х2+64х3+66х3+68х3+70х9+72х6+74х7+76х11+78х5+80х4 | = | =72,3 (ударов в минуту) | |
Помимо указанного метода прямого расчета средней арифметической взвешенной, существуют другие методы, в частности, способ моментов при котором несколько упрощены арифметические расчеты.
Расчет средней арифметической способом моментов проводится по формуле:
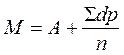 , где
, где
A – условная средняя (чаще всего в качестве условной средней берется мода Мо)
d – отклонение каждой варианты от условной средней (V–А)
Σdр — сумма произведений отклонений на их частоту.
Порядок вычисления представлен в таблице (за условную среднюю принимаем Мо = 76 ударам в минуту).
Определение средней арифметической способом моментов
| частота пульса V | Р | d (V–A) | dp |
| –16 | –16 | ||
| –14 | –28 | ||
| –12 | –36 | ||
| –10 | –30 | ||
| –8 | –24 | ||
| –6 | –54 | ||
| –4 | –24 | ||
| –2 | –14 | ||
| n = 54 | Σdp= –200 |
| M = 76 + | –200 | = 76–3,7 = 72,3 (ударов в минуту) |
Среднюю арифметическую можно также рассчитать и по данным середины группы. С учетом интервала между группами. Расчет проводим по формуле:
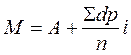
где i — интервал между группами.
Порядок вычисления представлен в табл. (за условную среднюю принимаем Мо = 73 ударам в минуту, где i = 3)
Определение средней арифметической способом моментов
| частота пульса V | середина группы | частота Р | условное отклонение в интервалах (d) | произведение условного отклонения на частоту (dp) |
| 60–62 | –4 | –12 | ||
| 63–65 | –3 | –9 | ||
| 66–68 | –2 | –12 | ||
| 69–71 | –1 | –9 | ||
| 72–74 | ||||
| 75–77 | ||||
| 78–80 | ||||
| n = 54 | Σ dp = –13 |
| M = 73 + | –13х3 | = 73–0,7 = 72,3 (ударов в минуту) |
Таким образом, полученное значение средней арифметической величины по способу моментов идентично таковому, найденному обычным способом.
Date: 2015-06-06; view: 1228; Нарушение авторских прав