Решение пределов через раскрытие неопределённостей

Неопределённость вида и вида 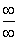- самые распространённые неопределённости, которые требуется раскрывать при решении пределов.

Большая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.

Неопределённость вида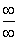

Пример 1. Раскрыть неопределённость 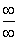и найти предел .

Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :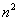

.

Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или "супермалому числу".

Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .

Пример 2. Раскрыть неопределённость 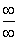и найти предел .

Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:

.

Комментарий к ходу решения. В числителе загоняем "икс" под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо "икса".

Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.

Неопределённость вида

Пример 3. Раскрыть неопределённость и найти предел .

Решение. В числителе - разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:

.

В знаменателе - квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):

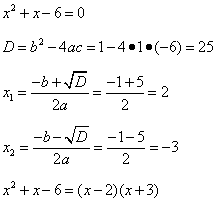
Запишем выражение, полученное в результате преобразований и найдём предел функции:

Пример 4. Раскрыть неопределённость и найти предел

Решение. Теорема о пределе частного здесь неприменима, поскольку

Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:

Пример 5. Раскрыть неопределённость и найти предел

Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:

Пример 6. Вычислить

Решение: воспользуемся теоремами о пределах

Ответ: 11

Пример 7. Вычислить

Решение: в этом примере пределы числителя и знаменателя при равны 0:

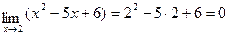; . Получили , следовательно, теорему о пределе частного применять нельзя.

Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3.

Квадратный трехчлен в числителе разложим по формуле , где x₁ и х₂ – корни трехчлена. Разложив на множители и знаменатель, сократим дробь на (x-2), затем применим теорему 3.

Ответ:

Пример 8. Вычислить

Решение: При числитель и знаменатель стремятся к бесконечности, поэтому при непосредственном применении теоремы 3 получаем выражение , которое представляет собой неопределенность. Для избавления от неопределенности такого вида следует разделить числитель и знаменатель на старшую степень аргумента. В данном примере нужно разделить на х:

Ответ:

Пример 9. Вычислить

Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. х³:

Ответ: 2

Пример 10. Вычислить

Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. х⁵:

=

числитель дроби стремится к 1, знаменатель к 0, поэтому дробь стремится к бесконечности.

Ответ:

Пример 11. Вычислить

Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. х⁷:

Ответ: 0

Date: 2015-11-15; view: 1229; Нарушение авторских прав