Задача № 315

Контрольная работа № 6.

Вариант 5

Задача № 305.

а) Решить задачу Коши для дифференциального уравнения первого порядка:

;

Решение:

Преобразуем уравнение к виду , .

Полагаем, что 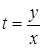, тогда

Подставляя это выражение в уравнение, получим:

Это уравнение с разделяющимися переменными.

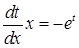
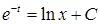
Делаем обратную замену:

- общее решение исходного дифференциального уравнения.

Найдем используя начальные условия .

Итак, окончательно получим:

б) Найти общее решение дифференциального уравнения второго порядка:

Решение:

В уравнение не входит . Обозначим . Тогда

Исходное уравнение примет вид:

Это уравнение с разделяющимися переменными.

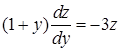
Делаем обратную замену:

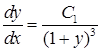
Итак, общее решение исходного дифференциального уравнения:

Задача № 315.

Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее начальным условиям:

; ;

Решение:

Это линейное неоднородное уравнение второго порядка с постоянными коэффициентами.

Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения данного неоднородного уравнения.

Для данного уравнения однородным уравнением является уравнение

Составляем характеристическое уравнение:

Общее решение соответствующего однородного уравнения:

Рассмотрим правую часть:

Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: f(x) = e^αx(P(x)cos(βx) + Q(x)sin(βx)),

(где P(x), Q(x) - некоторые полиномы) имеет частное решение:

y(x) = x^ke^αx(R(x)cos(βx) + S(x)sin(βx))

где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).

Для нашей задачи P(x) =0, Q(x) = 52, α = 0, β = 2.

Число α + βi = 2i не является корнем характеристического уравнения.

Итак, уравнение имеет частное решение вида:

Вычисляем производные:

которые подставляем в исходное дифференциальное уравнение:

Получим систему:

Частное решение имеет вид:

Общее решение исходного уравнения:

Найдем решение задачи Коши ; .

Окончательно получаем:

Date: 2015-11-15; view: 322; Нарушение авторских прав