
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Об искусстве рассуждения
|
|
Э. Кондильяк
Я изложил способности души, рассмотрел с Вами в общем виде различные обстоятельства, через которые прошел человек. Вы увидели происхождение правлений, законов, искусств и наук; Вы увидели предрассудки, заблуждения и первые успехи ума; Вы удивлялись то ограниченности, то обширности нашего разума 1. Это, Ваше высочество, должно научить Вас не доверять самому себе. Вы — человек и можете ошибаться, хотя Вы и принц; или, скорее, так как Вы принц, вы должны ошибаться больше, чем кто-либо другой. Лесть, которая осаждает Вас с колыбели и ждет лишь момента, чтобы усилить свою осаду, не заинтересована в том, чтобы открыть Вам глаза. Я отдаю Вам должное: Вы не любите, когда Вам льстят. Я всегда буду это помнить, и помните об этом Вы сами; Вы не раз краснели от похвал, которые Вы считали незаслуженными. Хотите отогнать льстецов? Для этого есть только одно средство: будьте более просвещенным, чем они. Для Вас было бы унизительным быть игрушкой в руках каких-то льстецов.
До сих пор я старался делать так, чтобы Вы рассуждали; сейчас речь идет о том, чтобы показать Вам все искусство рассуждения. Давайте же посмотрим, каковы в общем предметы наших знаний и какая степень достоверности доступна нашим знаниям.
| История природы делится на науку о чувственных истинах и науку об абстрактных истинах |
В сущности, есть только одна наука — история природы 2; эта наука слишком обширна для нас, и мы можем постигнуть лишь некоторые ее ветви.
Мы либо наблюдаем факты, либо комбинируем абстрактные идеи. Поэтому история природы делится на науку о чувственных истинах, физику, и на науку об абстрактных истинах, метафизику.
Я разделяю историю природы на науку о чувственных истинах и на науку об абстрактных истинах, потому что
принимаю во внимание лишь основные предметы, которыми мы можем заниматься. Каков бы ни был предмет наших исследований, для постижения связей чувственных идей необходимы абстрактные рассуждения; а чувственные идеи необходимы нам, чтобы составлять абстрактные идеи, давать им определение. Таким образом, видно, что уже с момента первого своего разделения обе эти ветви науки входят друг в друга; поэтому они оказывают друг другу помощь, и напрасно философы пытаются поставить между ними барьеры. Для умов ограниченных, как наши, весьма разумно рассматривать каждую из них отдельно; но было бы нелепо заключать, что они должны по своей природе существовать раздельно. Всегда нужно помнить, что есть в сущности только одна наука, и если мы познаем истины, которые кажутся нам оторванными друг от друга, то потому, что мы не знаем связи, которая объединяет их в одно целое.
| Метафизика охватывает все предметы нашего познания |
Из всех наук метафизика лучше всего охватывает все предметы нашего познания; она является одновременно наукой о чувственных истинах и наукой об абстрактных истинах. Наукой о чувственных истинах — потому что эта наука о том, что имеется в нас чувственного, как физика есть наука о том, что имеется чувственного вне нас 3; наукой об абстрактных истинах — потому что именно она открывает принципы, образующие системы, и дает все методы рассуждения. Сама математика является лишь ее ветвью. Стало быть, она ведает всеми нашими знаниями и ей принадлежит эта прерогатива, ибо если необходимо говорить о науках в соотнесении с нашим способом постигать, то именно метафизике, единственной науке, познающей человеческий ум, надлежит руководить нами в изучении всякого знания. Все в некоторых отношениях находится в ее ведении. Метафизика — самая абстрактная наука; она возвышает нас над тем, что мы видим и чувствуем; она возвышает нас до бога и образует науку, которую мы называем естественной теологией.
| Две метафизики: метафизика чувства и метафизика размышления |
Когда метафизика имеет своим единственным предметом человеческий ум, можно различить два ее вида: метафизику размышления и метафизику чувства. Первая исследует все наши способности; она усматривает, какова их первооснова и как они формируются, и соответственно пред-
писываст правила для руководства ими; этой метафизикой овладевают лишь благодаря обучению. Вторая чувствует наши способности; она повинуется их действию и следует принципам, которых она не знает; ею обладают, хотя, казалось бы, ее не приобретали, потому что счастливые обстоятельства сделали ее естественной; она — удел настоящих умов; она есть, так сказать, их инстинкт. Следовательно, метафизика размышления — это только теория, развивающая в своем принципе и в его следствиях все, что метафизика чувства осуществляет на деле. Например, метафизика чувства создает языки; метафизика размышления объясняет их систему; первая создает ораторов и поэтов; вторая дает теорию красноречия и поэзии.
| Три рода очевидности |
Я различаю три рода очевидности:
очевидности очевидность факта, очевидность чув
ства, очевидность разума *.
Мы имеем очевидность факта всякий раз, когда убеждаемся в фактах благодаря нашему собственному наблюдению. Если мы не наблюдали их сами, мы судим о них по свидетельству других, и это свидетельство в большей или меньшей степени заменяет очевидность.
Хотя Вы не были в Риме, Вы не можете сомневаться в существовании этого города; но у Вас могут быть сомнения относительно времени и обстоятельств его основания. Значит, среди фактов, о которых мы судим согласно свидетельству других людей, есть такие, которые выступают как очевидные или в которых мы уверены, как если бы сами их наблюдали; среди них есть и весьма сомнительные факты, тогда предание, которое их сообщает, является более или менее достоверным сообразно природе фактов, характеру свидетелей, одинаковости их сообщений и тому, насколько эти сообщения соответствуют обстоятельствам.
Вы способны на ощущения — вот то, в чем вы уверены благодаря очевидности чувства. Но в чем можно убедиться, располагая очевидностью разума? В тождестве. Два плюс два равно четырем — истина очевидная в силу очевидности разума, так как это предложение в сущности есть то же самое, что и предложение два плюс два равно двум плюс два. Первое и второе предложения отличаются друг от друга только выражением.
Я способен испытывать ощущения; Вы не сомневаетесь в этом, и, однако, у Вас нет в этом отношении ни одной из
трех очевидностей. У Вас нет очевидности факта, ибо Вы не можете сами наблюдать мои ощущения. Но этой же причине у Вас нет очевидности чувства, так как я один чувствую ощущения, которые я испытываю. Наконец, у Вас нет очевидности разума, потому что предложение «Я имею ощущения» не тождественно ни одному из предложений, какие Вам известны с очевидностью.
Свидетельство других людей восполняет очевидность чувства и очевидность разума, так же как и очевидность факта. Я говорю Вам, что у меня есть ощущения, и Вы в этом не сомневаетесь. Геометры Вам говорят, что сумма углов треугольника равна двум прямым, и Вы также этому верите.
За неимением трех очевидностей и свидетельства других людей, мы судим еще и по аналогии. Вы замечаете, что я имею органы, подобные Вашим, и поступаю как Вы, соответственно действию предметов на мои органы чувств. Из этого Вы заключаете, что если Вы сами имеете ощущения, то я также их имею. Ведь замечать отношения сходства между явлениями, которые наблюдают, и удостоверяться благодаря этому в явлении, которое нельзя наблюдать, — это и есть то, что называется «судить по аналогии».
Вот все средства, которыми мы обладаем для приобретения знаний, так как или мы сами видим факт, или нам его сообщают, или мы удостоверяемся при помощи чувства в том, что происходит в нас, или открываем истину благодаря очевидности разума, или же, наконец, судим об одной вещи по аналогии с другой.
Чтобы объяснить Вам, Ваше высочество, эти различные способы судить и рассуждать, мне будет достаточно дать Вам поупражняться на разных примерах. Я приведу их немало и не буду при этом следовать никакому плану. Неважно, что я напишу для Вас трактат об искусстве рассуждения, важно, чтобы Вы рассуждали. Это искусство станет Вам известно, когда Вы достаточно поупражняетесь.
Однако дать Вам поупражняться на суждениях, которые выносятся согласно свидетельству других людей, будет невозможно. Вы еще недостаточно прочли, чтобы суметь рледовать за мной в подобном предприятии; мы сможем заняться этим лишь тогда, когда Вы изучите историю, или по мере того, как Вы будете ее изучать.
| * См. «Логика», ч. II, гл. 9. |
| КНИГА ПЕРВАЯ ГДЕ ТРАКТУЕТСЯ О РАЗЛИЧНЫХ СПОСОБАХ УБЕЖДАТЬСЯ В ИСТИНЕ |
| ГЛАВА I |
| Тождество есть признак очевидности разума |
Чтобы хорошо рассуждать, необходимо точно знать, что такое очевидность, и уметь узнавать се по одному признаку, который полностью исключает всякого рода сомнения.
Предложение является очевидным или само по себе, или поскольку оно представляет собой очевидное следствие другого предложения, которое очевидно само по себе 4.
Предложение очевидно само по себе, когда тот, кто знает значение слов, не может сомневаться в том, что оно утверждает; таково предложение Целое равно своим частям, вместе взятым.
Почему же тот, кто в точности знает идеи, которые связывают с различными словами этого предложения, не может сомневаться в его очевидности? Потому что он видит, что оно тождественно, что оно не означает ничего, кроме того, что целое равно самому себе.
Если говорят: Целое больше, чем одна из его частей, то это опять-таки тождественное предложение, ибо это значит сказать, что целое больше, чем то, что меньше его.
Следовательно, тождественность есть признак, по которому узнают, что предложение является очевидным само по себе; а тождественность распознается, когда предложение может быть переведено в выражения, сводящиеся к формуле то же самое есть то же самое (le meme est le meme).
Стало быть, предложение, очевидное само по себе, — это предложение, тождественность которого усматривается непосредственно в выражающих его словах.
Из двух предложений одно является очевидным следствием другого, когда из сравнения слов видно, что они
утверждают одно и то же, т. е. когда они тождественны.
Значит, доказательство — это ряд предложений, и которых
одни и те же идеи, переходя из одного предложения в
другое, различаются лишь тем, что они по-разномы вы-
ражены, а очевидность рассуждения состоит исключительно в тождественности.
| Пример, доказывающий это |
| ОБ ОЧЕВИДНОСТИ РАЗУМА |
Предположим, что нужно доказать такое предложение: Площадь (mesurе) всякого треугольника есть произведение его высоты на половину его основания.
Конечно, в этих выражениях не видно тождества идей. Значит, это предложение не является очевидным само по себе; значит, его нужно доказать, нужно показать, что оно — очевидное следствие очевидного предложения, или что оно тождественно тождественному предложению; нужно показать, что идея, которую я должен составить себе о площади всякого треугольника, — это та же самая идея, которую я должен иметь о произведении высоты всякого треугольника на половину его основания.
Для этого есть только одно средство, а именно сначала точно объяснить идею, которую я связываю со словами «измерить площадь», а затем сравнить эту идею с той идеей, которую я имею о произведении высоты треугольника на половину основания.
Но измерить площадь — это то же самое, что последовательно наложить на все ее части другую площадь определенной величины, например квадратный фут. Здесь тождественность заметна уже при одном взгляде на слова. Значит, это предложение относится к числу тех, которые нет нужды доказывать.
Но я не мог бы непосредственно приложить к треугольной поверхности определенное число квадратных поверхностей одинаковой величины, и здесь-то доказательство становится необходимым, т. е. мне нужно путем ряда тождественных предложений прийти к открытию тождественности предложения Площадь всякого треугольника есть произведение его высоты на половину его основания. Может быть, сначала это покажется Вам очень трудным, однако нет ничего проще этого.
Сначала я хочу обратить Ваше внимание на то, что знать измерение какой-нибудь величины и знать ее отношение к величине, размер которой известен,— одно и то же; например, нет разницы между знанием того, что величина данной площади — один квадратный фут, и знанием того, что она есть половина площади, о которой известно, что ее величина — два квадратных фута.
После этого Вы легко поймете, что если мы находим площадь, на которую мы могли бы наложить последова-
тельно определенное число квадратных площадей одинаковой величины, то тотчас же, как мы откроем отношение величины площади треугольника к величине площади, которую мы измерили, мы узнаем размер площади треугольника.
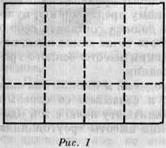
Возьмем для этого прямоугольник (рис. 1), т. е. поверхность, ограниченную четырьмя перпендикулярными линиями. Вы видите, что можете рассматривать его как составленный из нескольких маленьких площадей одной и
|
той же величины; все они одинаково ограничены перпендикулярными прямыми. Вы видите также, что все эти маленькие площади, взятые вместе,— это то же самое, что и целая поверхность всего прямоугольника.
Ведь нет разницы между тем, чтобы разделить прямоугольник на одинаковые квадратные площади или наложить последовательно на все его части площадь определенной величины.
Итак, я рассматриваю разделенный таким образом прямоугольник и вижу, что число квадратных футов, которое он имеет, в высоту, повторяется столько раз, сколько футов содержит его основание. Если на первом футе своего основания он имеет в точности три квадратных фута высоты, то он имеет также в точности три квадратных фута на втором, на третьем и на всех других. Эта истина заметна на глаз, но ее легко проверить при помощи тождественных предложений.
В самом деле, прямоугольник представляет собой площадь, четыре стороны которой перпендикулярны друг другу. У площади, стороны которой перпендикулярны, противоположные стороны параллельны, т. е. одинаково удалены друг от друга во всех противоположных точках своей длины.
Площадь, противоположные стороны которой одинаково удалены во всех точках, противоположных ее длине, имеет одинаковую высоту по всей длине своего основания. Площадь, имеющая одинаковую высоту по всей длине своего основания, имеет столько же футов в высоту, сколько ее основание имеет футов в длину.
Все эти предложения тождественны. Они суть лишь различными способами выраженное предложение Прямоугольник есть прямоугольник.
Следовательно, измерить прямоугольник, наложить последовательно на все части его поверхности площадь определенной величины, разделить его площадь на равные квадраты, взять число футов, которое он имеет в высоту, столько раз, сколько футов имеет в длину его основание, — это значит сделать одно и то же несколькими различными способами.
Если это так, то больше нет необходимости ни в том, чтобы делить площадь на маленькие квадраты, ни в том, чтобы последовательно накладывать на различные части площадь определенной величины; взяв число футов в высоту столько раз, сколько имеется футов в основании, мы получим точные размеры данной площади.
Таким образом, можно заменить предложение Измерить прямоугольник — значит взять число футов, которое он имеет в высоту, столько раз, сколько он имеет футов в основании предложением, с которого мы начали: Измерить прямоугольник — значит последовательно наложить на его различные части площадь определенной величины.
В самом деле, взглянув на эти выражения, мы не узнали, что эти два предложения являются по существу одним предложением, но тождество не могло от нас ускользнуть, когда мы стали его разыскивать в ряде промежуточных предложений. Мы видели, что одна и та же идея переходит из одних предложений в другие, а изменяется лишь способ, которым она выражается.
Доказать — значит осуществить перевод очевидного предложения, придавая ему различные формы до тех пор, пока оно не станет предложением, которое требуется доказать. Это значит изменять слова, которыми выражено предложение, и прийти через посредство ряда тождественных предложений к заключению, тождественному тому предложению, из которого оно непосредственно выводится. Нужно, чтобы тождественность, незаметная, когда проходят через промежуточные предложения, была бы явной при одном только взгляде на выражения, когда непосредственно переходят от одного предложения к другому.
Предложение, которое мы только что доказали: Измерить прямоугольник — значит взять число футов, которое он имеет в высоту, столько раз, сколько футов содержится в его основании — это то же самое, что умножить его высо-
ту на основание, а это опять-таки то же самое, что взять произведение его высоты на его основание.
Предложение же Площадь прямоугольника есть произведение его высоты на его основание есть правило, от которого следует идти путем ряда предложений, всегда тождественных друг другу, вплоть до самого вывода: Площадь всякого треугольника есть произведение его высоты на половину основания.
Но я уже отметил, что если нам известна площадь прямоугольника, то мы найдем площадь треугольника, когда узнаем отношение одной из этих фигур к другой, ибо нет разницы между знанием площади фигуры и знанием того, как относится площадь данной фигуры к уже известной площади какой-либо фигуры.

|
Прямоугольник (рис. 2). разделенный по диагонали, дает два треугольника, площади которых, взятые вместе, равны его площади. Ведь сказать, что эти две площади равны площади прямоугольника, — то же самое, что сказать, что два треугольника были образованы из прямоугольника при помощи диагонали, которая делит его пополам. Кроме того, Вы заметите, что поверхности этих двух треугольников равны; Вы даже на глаз видите истинность этого предложения; но нужно доказать Вам их тождественность.
Площадь [фигуры] определяется величиной прямых, которые ее ограничивают, и величиной углов, образуемых этими прямыми. Следовательно, в двух выражениях: две площади равны и две площади ограничены равными прямыми, образующими одинаковые углы — содержится только одно предложение, выраженное двумя способами. Следовательно, предложения Площади двух треугольников равны и Стороны этих треугольников равны опять-таки суть два тождественных предложения. Два треугольника, которые содержат в себе прямоугольник, разделенный по диагонали, имеют, стало быть, равные площади, если их стороны равны и если они образуют одинаковые углы.
Ведь сказать, что два треугольника заключены таким образом в прямоугольнике,— это то же самое, как если бы
мы сказали, что они имеют одну общую сторону — диагональ прямоугольника — и что они имеют также одинаковое основание и одинаковую высоту, образуя одинаковые углы, т. е. сказать, что они имеют три равные стороны и равные площади, или, короче, равны во всем.
Но сказать, что они равны во всем,— значит сказать, что каждый из двух треугольников относится к прямоугольнику как половина к целой единице, а это предложение есть не что иное, как перевод предложения Прямоугольник разделен на два равных треугольника.
Ведь высказывание Поверхность треугольника относится к поверхности прямоугольника, имеющего то же основание и ту же высоту, что и данный треугольник, как половина к целому и высказывание Площадь такого треугольника представляет собой половину площади этого прямоугольника представляют собой по смыслу выражений два тождественных предложения.
Но мы видели, что площадь прямоугольника есть произведение высоты на основание; значит, предложение Площадь этого треугольника есть половина площади данного прямоугольника будет тождественно предложению Площадь этого треугольника есть половина произведения его высоты на основание, или, как обычно выражаются, произведение высоты на половину основания.
Предстоит лишь узнать, равна ли площадь всякого другого вида треугольника произведению высоты на половину основания.
Какова бы ни была форма треугольника, площадь которого хотят узнать, из его вершины можно опустить перпендикуляр и этот перпендикуляр опустится на основание либо внутри треугольника, либо вне его.
Если он опустится внутри треугольника (рис. 3), он разделит его на два треугольника, у каждого из которых две стороны взаимно перпендикулярны и которые, следовательно, являются треугольниками того же рода, что и треугольник, который мы измерили. Значит, площадь каждого из них равна половине произведения высоты на основание.
Однако узнать суммарную площадь двух треугольников — то же самое, что узнать площадь треугольника, который мы разделили, опустив перпендикуляр. Эта площадь остается одной и той же, заключена ли она в одном треугольнике или разделена пополам. Значит, сказать ли, что площадь большого треугольника равна половине произведения его высоты на его основание, или сказать о

|
| двух малых треугольниках [из которых он состоит], что она равна половине произведения их высоты на их основание,— это одно и то же. |

Если перпендикуляр (рис. 4) опускается вне треугольника, нужно продолжить основание до точки, где встретятся эти две прямые, и мы образуем треугольник того же вида, что и треугольник, который мы измерили сначала.
Благодаря этой операции Вы получаете два треугольника, заключенные в одном, и Вы видите, что площадь большого треугольника равна сумме площадей двух малых треугольников, на которые он разделен.
Следовательно, одно и то же, измерить ли эту площадь, взяв половину произведения высоты большого треугольника на его основание, или взяв раздельно половины произведений высоты каждого из двух малых треугольников на их основания. Эти две операции сводятся к одному и тому же, и здесь нет иного различия, кроме того, что в одной операции делается в два приема то, что в другой делается сразу.
Таким образом, явно выступает тождество двух следующих предложений: Площадь большого треугольника, который мы образовали, продолжая основание до перпендикуляра, равна половине произведения его высоты на его основание; Площадь каждого из треугольников, заключенных в большом, равна половине произведения его высоты на его основание.
Но какую бы форму ни имел треугольник, Им всегда можете опустить из вершины перпендикуляр, который либо опустится внутри треугольника на его основание, либо, опустившись вне треугольника, разделит основание, которое Вы продолжили. Значит, Вы всегда можете убедиться при помощи ряда тождественных предложений, что его площадь равна половине произведения его высоты
на его основание. Значит, доказательство применимо ко всем треугольникам, и эта истина не допускает никакого исключения: Площадь всякого треугольника есть половина произведения его высоты на его основание.
| Другой пример, доказывающий, что тождество есть признак очевидности разума |
Я выбираю это предложение не только для того, чтобы привести пример; эта истина, Ваше высочество, послужит мне правилом, для того чтобы вести Вас к другим знаниям. При
помощи этого же правила я докажу Вам, что сумма трех углов треугольника равна двум прямым, ибо это еще одна истина, в познании которой мы нуждаемся.
Прямая есть линия, которая идет прямо от одной точки к другой. Это линия, направление которой не изменяется, или же линия, сохраняющая на всем своем протяжении направление, в каком она начинается; это наикратчайшая линия между двумя точками; это такая линия, что, когда поворачиваются ее крайние точки, вся она поворачивается так, что ни одна из ее частей не изменяет своего положения относительно других частей. Вы видите, что все эти выражения представляют собой лишь различные способы излагать одну и ту же идею и что они предполагают идею, которую они будто бы определяют.
Когда речь идет об идее, составленной из нескольких других идей, она определяется легко, так как для этого достаточно выразить идеи, из которых она образована. Говоря, например, что треугольник есть площадь, ограниченная тремя прямыми, дают его определение; и это определение носит характер, весьма отличный от мнимых дефиниций, даваемых прямой линии. В самом деле, дефиниция треугольника дала бы его идею тому, кто никогда не замечал ни одного треугольника; напротив, дефиниции прямой не дали бы ее идеи тому, кто никогда не замечал никакой прямой линии.
Дело в том, что идеи, когда они просты, не приобретаются при помощи дефиниций, а происходят исключительно из чувств. Проведите линию при помощи компаса — это будет кривая линия; проведите ее с помощью линейки, и это будет прямая линия. Правда, ничто не убедит Вас в том, что эта линия действительно прямая, так как ничто не убедит Вас, что сама линейка прямая; но, в конце концов, прямая линия — это то, чем Вам кажется линия, проведенная с помощью линейки; и хотя эта видимость может быть ложной, она тем не менее является идеей пря-
мой линии. Рассматривая прямую и кривую линии, Вы можете заметить, что вторая образована из нескольких линий, которые пересеклись бы, если бы они были продолжены. Но когда Вы скажете: «прямая линия — одна, кривая линия состоит из многих», Вы не дадите определение ни той, ни другой. Вы видите, что есть вещи, которым не следует даже и помышлять дать определение *.
Прямая перпендикулярна другой прямой, когда она не отклоняется ни в какую сторону, или когда она не наклонна, когда она с обеих сторон образует два равных угла, два прямых угла, два угла, каждый из которых имеет 90 °, или измеряется четвертью окружности. Все это лишь синонимические и тождественные выражения для того, кто знает значение слов.
Прямая является наклонной, когда ее направление отклоняется от направления другой прямой, когда, будучи продолжена до точки, где она встречается с этой другой прямой, она составила бы с ней два неравных угла, два угла, один из которых имел бы более, а другой — менее 90 °.
Две прямые параллельны, когда по всей их длине точки одной прямой одинаково удалены от соответствующих точек другой, или когда все прямые, проведенные из точек одной прямой в соответствующие точки другой, имеют совершенно одинаковую длину.
Вы заметите прежде всего, что положение прямой линии есть лишь отношение ее направления к направлению другой линии и что, следовательно, если дано ее направление, то ее положение определено.
Во-вторых, Вы заметите, что одна прямая может занимать по отношению к другой прямой лишь три положения: она или перпендикулярна ей, или наклонна к ней, или ей параллельна. Наконец, Вы заметите, что положение одной прямой по отношению к другой является взаимным: если одна параллельна другой, то и другая ей параллельна; если одна перпендикулярна другой, то и другая ей перпендикулярна; если одна наклонна к другой, то и другая к ней наклонна и каждая из них образует с другой одни и те же углы. Достаточно взглянуть на термины, в них употребляе-
* Со времени первого издания моего «Курса обучения» я показал в моей «Логике», что вещи познаются только благодаря анализу и что дефиниции ограничиваются тем, что указывают на вещи. Всякая дефиниция, предполагающая, что вещь известна, является скорее дефиницией слова, чем дефиницией вещи 5.
мые, и мы увидим, что все эти предложения тождественны и, следовательно, не относятся к числу тех, которые следует пытаться доказать. Нам остается дойти путем ряда тождественных предложений до заключения, что сумма трех углов треугольника равна двум прямым.
Предположить, что прямая EG (рис. 5) является перпендикуляром, опущенным на прямую АВ,— значит предположить, что она образует с прямой АВ два равных угла, или два прямых угла.

Предположить, что эта прямая продолжена вниз от прямой АВ,— значит предположить, что она продолжена в направлении прямой EF. Следовательно, если мы предположим, что прямая EF является этим продолжением, мы тем самым признаем, что прямая GF, так же как и прямая EF, образует с прямой АВ два прямых угла, ибо, если бы два угла были неравными, один был бы больше прямого угла, а другой — меньше. А это означало бы, что прямая GF была бы наклонной; значит, она не была бы продолжением прямой EG, что противоречит предположению, из которого мы исходим.
Стало быть, как в своей нижней части, так и в своей верхней части прямая EF перпендикулярна прямой АВ, а сказать так — то же, что сказать, что прямая АВ перпенди-кулярна прямой EF, поскольку предположить, что прямая АВ наклонна к прямой EF, означало бы предположить, что прямая EF наклонна к прямой АВ, поскольку прямые занимают по отношению друг к другу одинаковое положение.
Но прямая EF, будучи продолжена до точки Н, следует направлению, заданному двумя точками Е, G, и является прямой по всей своей длине.
Если это так, то сказать, что прямая CD параллельна прямой АВ,— значит сказать, что она образует с пря-
мой ЕН углы, подобные углам, которые образует прямая АВ с той же самой прямой; а сказать, что она образует два подобных угла,— значит сказать, что она образует прямые углы. В самом деле, если бы мы допустили противоположное, мы допустили бы, что она наклонна по отношению к прямой ЕН; а предположив в ней наклон, которого лишена прямая АВ, мы допустили бы, что она не параллельна прямой АВ.
Ведь сказать, что прямая CD образует с прямой ЕН прямые углы,— значит сказать, что прямая ЕН образует прямые углы с прямой CD, а сказать, что прямая ЕН образует прямые углы с прямой CD,— значит сказать, что она образует прямые углы с прямой АВ. Таким образом, доказано, что прямая, перпендикулярная другой прямой, перпендикулярна всем прямым, параллельным этой второй прямой, или что она образует со всеми прямыми, параллельными последней, прямые углы.
Следовательно, если эта прямая наклонна к одной из параллельных, она будет одинаково наклонна ко всем другим параллельным, ибо предположить, что она не одинаково к ним наклонна,— значит предположить, что она не прямая или что прямые, которые она пересекает, не параллельны.
Следовательно, прямая FG одинаково наклонна к прямой АВ (рис. 6) и к прямой CD. Ведь сказать, что она одинаково наклонна к обеим,— значит сказать, что она образует с той стороны, в которую она отклоняется, равные углы на каждой параллели; что угол q, внешний двум параллелям, равен внутреннему углу и и что внутренний угол s равен внешнему углу у.
Очевидно также, что с другой стороны прямой FG внешний угол р равен внутреннему углу t, а внешний угол х — внутреннему углу r. Чтобы сделать это явным, нужно лишь перевернуть рисунок.
Впрочем, если на первом рисунке прямая, которая перпендикулярно пересекает две параллели, образует на каждой два прямых угла, то на втором рисунке прямая, пересекающая их наклонно, образует на каждой два угла, сумма которых равна двум прямым. Ибо наклонность линии FG, образующая, например, угол q, не равный углу р, не может изменить суммарную величину этих двух углов. В самом деле, чтобы заметить тождество суммы двух углов на втором рисунке и суммы двух углов на первом, достаточно принять во внимание, что на обоих рисунках
Величина рассматриваемых нами двух углов равна полу-Окружности.
Значит, угол р равен двум прямым минус угол q; аналогичным образом угол t равен двум прямым минус угол и, ведь угол и равен углу q. Таким образом, каждый из углов p и t равен одной и той же величине; следовательно, они равны друг другу.
Та часть прямой FG, которая находится выше линии АВ, наклонена в сторону В, а нижняя часть ее наклонена в сторону А. Ведь предположить, что эти две линии прямые,— значит предположить, что, как в той своей части, которая выше АВ, так и в той, которая ниже АВ, прямая FG имеет одинаковый наклон; если бы он не был одинаковым, одна из двух линий не была бы прямой.
Но сказать, что наклон одинаков,— значит сказать, что прямая FG со стороной А образует угол, равный углу, который она образует со стороной В, и угол rравен углу q. Таким же путем можно будет доказать, что угол р равен углу s, угол t равен углу y, угол и — углу х. Это накрест-лежащие углы; следовательно, накрестлежащие углы равны.
В самом деле, очевидно, что угол гравен двум прямым минус угол р, а угол q равен двум прямым минус угол р. Значит, каждый из них равен двум прямым за вычетом одной и той же величины. Следовательно, они равны друг ДРУгу.

|
Ведь сказать, что угол rравен накрестлежащему углу q,— значит сказать, что он равен всякому углу, которому равен сам угол q. Но мы видели, что угол q равен углу и. Значит, угол rравен углу и. На том же основании угол s равен углу t, угол р — углу у, угол q — углу х. Именно это и выражают, говоря, что противолежащие углы равны. Предположим теперь, что прямая FG (рис. 7) параллельна прямой de. Вы видите два противолежащих угла а и d и два других — с и е. Значит, угол а равен углу d, а угол с — углу е. Ведь сумма углов а, Ъ, с равна двум прямым. Значит, три угла треугольника равны двум прямым углам.
Двух примеров, которые я привел в этой главе, более чем достаточно, для того чтобы сделать понятным, что
| очевидность разума состоит исключительно в тождестве. К тому же я, как и предупреждал, выбрал их потому, что это две истины, которые поведут нас к другим истинам. |
| ГЛАВА II РАССУЖДЕНИЯ О МЕТОДЕ, ИЗЛОЖЕННОМ В ПРЕДЫДУЩЕЙ ГЛАВЕ |
| Каким образом тождество замечают в ряде предложений |
Вы ясно видите, что вся сила доказательства теоремы о площади треугольника заключается исключительно в тождестве. Обратите внимание, что мы начали с дефиниции слова измерять, что эта дефиниция содержится во всех следующих предложениях и что при переходе от одного предложения к другому изменяется лишь форма рассуждения. А эта дефиниция высказывается лишь в других выражениях.
Невозможность непосредственно сравнить дефиницию слова измерять и дефиницию слова треугольник — вот что поставило Вас перед необходимостью предпринять в речи различные преобразования одной и той же идеи.
Но чтобы пройти таким образом через ряд следующих друг за другом предложений и открыть тождество первой дефиниции с заключением рассуждения, необходимо в совершенстве знать все вещи, которые Вам нужно сравнивать. Вы не докажете теорему о площади треугольника, если не имеете точных и полных идей того, что такое измерять прямоугольник, площадь, сторона, диагональ. Составьте же полные идеи каждой фигуры, и среди них не окажется такой, какую Вы не смогли бы точно измерить. Метод, которому мы следовали, применим ко всем случаям, когда мы не испытываем недостатка в идеях; и Вы можете предвидеть, что все математические истины суть лишь различные выражения этой первоначальной дефиниции.
Измерять — значит последовательно прилагать ко всем частям измеряемой величины определенную величину. Таким образом, математика представляет собой необозримую по своему объему науку, которая заключается в идее, выражаемой одним словом.
Нельзя всегда, как в примере, который я Вам только что привел, проделать с первой дефиницией все необходимые преобразования; но есть методы, позволяющие преодолеть эту трудность; чего невозможно сделать с целой идеей, можно последовательно проделать со всеми ее частями.
| Тождество явственно выступает в арифметике |
Например, большое число может быть выражено только одним способом, и арифметика не предоставляет средства варьировать его выражение. Но если, рассматривая непосредственно два больших числа, я не могу установить, в чем они тождественны, я могу открыть тождество, существующее между их частями, и благодаря этому способу я узнаю все их отношения. Именно на этом и основаны четыре действия арифметики, которые можно даже свести к двум — сложению и вычитанию. Стало быть, когда я говорю шесть плюс два равно восьми, это то же, как если бы я сказал шесть плюс два равно шести плюс два; а когда я говорю шесть минус двй равно четырем, это опять-таки то же самое, как если бы я сказал шесть минус два равно шести минус два, и т. д.
Значит, арифметическая очевидность состоит в тождестве, и, если шести и двум я даю наименование восьми, а шести минус два — наименование четырех, я изменяю выражение лишь для того, чтобы облегчить сравнения и сделать тождество заметным.
Таким образом, доказательства всегда производятся лишь при помощи ряда тождественных предложений, производим ли мы действия с целыми идеями или последовательно с каждой их частью 7.
Этого довольно, чтобы показать Вам, что очевидность разума относится исключительно к тождеству идей.
ГЛАВА III
Date: 2015-11-13; view: 367; Нарушение авторских прав