Сурет. Графтар

Мұндай схемаларды графтар деп атайды. А, Б, В, Г, Д, Е нүктелері графтың төбелері, оларды қосатын кесінділер графтың қабырғалары деп атайды. Граф қабырғаларының қиылысу нүктелері оның төбелері болып табылмайтының ескерте кетейік. Шатастырып алмау үшін граф төбелерін көбінесе нүктелермен емес, кішкентай дөңгелектермен кескіндейді. Қабырғаны көбінесе түзу сызықты кескінділермен емес, қисық сызықты кескінділермен – «доғалармен» кескіндеген ыңғайлы болады.

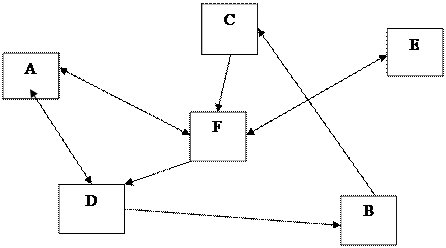
Ал енді есебімізге оралайық. Бұған дейін өткізілген ойындар саны қабырғалар санына тең, яғни 7. Өткізілуге тиісті ойындардың санын табу үшін, тағы бір граф сызайық, оның төбелері бұрынғыдай, бірақ қабырғалары бір-бірімен әлі ойнамаған судентерді қосатын кесінділер болады, ол 2-суретте көрсетілген. Бұл графтың қабырғасы 8 болып шықты, демек, әлі 8 ойын өткізу керек: Айгүл – Тимурмен және Дамирмен, Бекжан – Тимурмен, Дамирмен және Тимурмен т.с.с. теннис ойнауы керек.

Графтарды біз өте жиі пайдаланамыз. Темір жолдардың схемасын қарастырсақ: мұнда бекет – графтың төбесі, бекеттер арасындағы жол учаскелері – графтың қабырғалары. Кубтың, пирамиданың т.с.с. төбелері мен қабырғалары да граф құрайды.

Графтар теориясы – біршама жас ғылым. Ньютон заманыңда мұндай ғылым болмағанымен, графтардың бір түрі болып табылатын «генеологиялық ағаштар» бар еді. Графтар жөніндегі алғашқы жұмыс Леонард Эйлерге тән, ол 1736ж Петербург Ғылым академиясы публицистикаларында жарияланды. Эйлер дөңгелектері логикалық есептерде пікірлердің ақиқаттығының жиындарын кескіндеуде қолданылады.

Математикада кез келген V жиыны мен V жиынының элементтерінің парларынан тұратын E бинарлық қатынасын граф деп атайды. Белгілеуі: G = (V, E). Егер E жиынының элементтерін реттелмеген парлар ретінде қарастырсақ, ондай графты бағытталмаған (симметриялы) деп, ал парлар оның қырлары деп аталады. Кері жағдайда граф бағытталған, ал E жиынының элементтері графтың доғалары деп аталады. (a, a) пары тұзақ деп аталады, егер Е жиынында (a, b) пары бірнеше рет кездессе, оны еселі қыр (доға) деп атайды. Тұзақсыз және еселі қырларсыз графты бағытталмаған (немесе жай ғана граф), тұзақсыз графты мультиграф, ал тұзақтар кездесетін мультиграфты псевдограф дейміз. Қыр арқылы жалғасқан граф төбелерін іргелес деп атайды. Егер қандай да бір төбе қырға тиісті болса, онда оларды инцидентті деп атайды.

Қырлары қайталанбайтын жолды тізбек деп атайды. Төбелері қайталанбайтын жол қарапайым тізбек деп аталады. Жолда 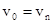болса, ол тұйық жол деп аталады. Қырлары қайталанбайтын тұйық жол цикл деп аталады. Төбелері қайталанбайтын тұйық жол қарапайым цикл деп аталады. Циклсыз байланған графты ағаш деп атайды.

Циклдардың жойылып кетуіне соқтыратын графтарды түрлендірудің бірнеше тәсілдері бар. Олар: аз мәнді байланыстардан өтіп кету, циклдық конструкцияларды бір төбеге біріктіру, тиісті түсініктерді қайта қалыптастыру, түсінікті байланыстыру.

Date: 2015-11-13; view: 1004; Нарушение авторских прав