
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Множественная регрессия
|
|
2. Необходимые сведения. Рассмотрим множественную линейную регрессионную модель с двумя объясняющими переменными
 ,
,
где a0, a1, a2 - неизвестные параметры, ε - случайная переменная (случайный член, случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерения.
Нахождение оценок неизвестных параметров в модели с тремя переменными x1, x2, y так же, как и в модели с двумя переменными, основывается на применении метода наименьших квадратов, основные этапы которого в этом случае сводятся к следующему.
1. Используя выборочные наблюдения над тремя переменными x1, x2, y, то есть: (xi1, xi2, yi), i=1, …,n, и уравнение регрессии 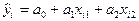 , в котором коэффициенты a0, a1, a2 пока неизвестны, составляются отклонения
, в котором коэффициенты a0, a1, a2 пока неизвестны, составляются отклонения  .
.
2. Определяется сумма квадратов отклонений
 ,
,
которая является некоторой функцией F трех переменных a0, a1, a2, т.е.
 .
.
3. Оценки a0, a1, a2 неизвестных параметров модели a0, a1, a2 находятся из условия минимума суммы квадратов отклонений, т.е. из условия
 .
.
4. Для нахождения точки минимума функции  записываются необходимые условия экстремума
записываются необходимые условия экстремума
 ,
, 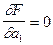 ,
,  .
.
5. Определяются частные производные функции  :
:
 ;
;
 ;
;
 .
.
6. Необходимые условия экстремума записываются еще один раз с учетом найденных выражений для частных производных  ,
,  ,
,  :
:
 ,
,
 ,
,
 .
.
7. После элементарных преобразований данная система уравнений записывается в виде так называемой системы нормальных уравнений, представляющую собой систему трех линейных уравнений относительно трех неизвестных a0, a1, a2:
 (2.1)
(2.1)
Найдем численные значения оценок a0, a1, a2 в рассматриваемой задаче. Обозначим:

 ,
,  ,
,  ,
,  .
.
Тогда
 ,
,  . (2.2)
. (2.2)
Обратим внимание, что почти все элементы матриц в (2.2) мы уже знаем (см. последнюю строку «сумма» таблицы 1.1). Не знаем только Σ xi1 xi2.
Система (2.1) в матричном виде запишется, как
 .
.
Ее решением будет вектор A:
 , (2.3)
, (2.3)
где  - матрица, обратная к матрице (
- матрица, обратная к матрице (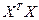 ).
).
Решение задачи. Используя последнюю строку «сумма» таблицы 1.1, в которой нами уже рассчитаны значения Σ xi1, Σ x2i1, Σ xi2, Σ x2i2 и др., а также отдельно дополнительно вычислив значение Σ xi1xi2 (в нашем примере оно равно 11095), получим:
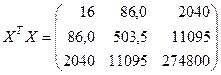 ,
,  .
.
Найдем матрицу  , обратную к матрице
, обратную к матрице 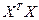 . Для этого сначала вычислим главный определитель:
. Для этого сначала вычислим главный определитель:


Определим матрицу алгебраических дополнений
 ,
,
где  . Здесь Mij -минор элемента, стоящего на пересечении i -й строки и j -го столбца матрицы
. Здесь Mij -минор элемента, стоящего на пересечении i -й строки и j -го столбца матрицы  . Например,
. Например,

 и т. д.
и т. д.
Окончательно получим
 .
.
Составляем так называемую присоединенную матрицу  ,
,
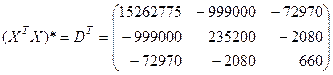 .
.
Отметим, что в данном случае DT=D, так как матрица D симметрична.
Наконец,
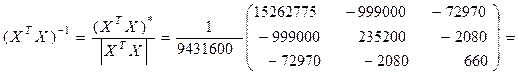
 . (2.4)
. (2.4)
По формуле (2.3) находим вектор оценок A:
 .
.
Таким образом,
 . (2.5)
. (2.5)
2.2. Необходимые сведения. Напомним, что важной характеристикой качества подбора уравнения регрессии является коэффициент детерминации R2. Для множественной регрессии R2 рассчитывается по той же формуле (1.9), что и в случае парной регрессии:
 .
.
Напомним, что здесь  - выборочное среднее, yi - выборочные значения зависимой переменной y,
- выборочное среднее, yi - выборочные значения зависимой переменной y,  - значения зависимой переменной, вычисленные по уравнению множественной регрессии
- значения зависимой переменной, вычисленные по уравнению множественной регрессии  . Левая часть равенства, т.е.
. Левая часть равенства, т.е.  интерпретируется как мера рассеивания переменной y относительно ее среднего значения
интерпретируется как мера рассеивания переменной y относительно ее среднего значения  . Эта мера раскладывается на две составляющие. Первая часть
. Эта мера раскладывается на две составляющие. Первая часть  - это мера разброса, «объясненная» с помощью уравнения регрессии. Вторая часть
- это мера разброса, «объясненная» с помощью уравнения регрессии. Вторая часть  - это мера разброса, «не объясненного» уравнением регрессии.
- это мера разброса, «не объясненного» уравнением регрессии.
Коэффициент детерминации R2, как и выше, определяется по формуле:
 , или
, или  .
.
Значение R2 характеризует ту долю дисперсии переменной y, которая обуславливается, или которую можно «объяснить» уравнением регрессии  . Если R2 равен 1, то имеет место полная корреляция с моделью, то есть нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминации равен 0, то уравнение регрессии неудачно для предсказания значений y.
. Если R2 равен 1, то имеет место полная корреляция с моделью, то есть нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминации равен 0, то уравнение регрессии неудачно для предсказания значений y.
Коэффициент детерминации R2 равен квадрату коэффициента множественной корреляции. Коэффициент множественной корреляции R определяется по формуле:
 .
.
Решение задачи. Для вычисления линии модели  , остатков ei и других переменных, необходимых расчета R2, нужно сформировать таблицу, аналогичную таблице 1.7, применявшуюся для парной регрессии. Для экономии места здесь она не приводится. Можно проверить, что для уравнения (2.4)
, остатков ei и других переменных, необходимых расчета R2, нужно сформировать таблицу, аналогичную таблице 1.7, применявшуюся для парной регрессии. Для экономии места здесь она не приводится. Можно проверить, что для уравнения (2.4)
 ;
;
 ;
;
 .
.
Коэффициент детерминации R2 =0,94. Следовательно, регрессия y на x1 и x2 объясняет 94% колебаний значений y. Это свидетельствует о значительном суммарном влиянии независимых переменных x 1 и x2 на зависимую переменную y.
Качество уравнения множественной регрессии, так же, как и парной, оценивает F-тест. Напомним, что он основан на проверке гипотезы H0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Фактическое значение F- статистики Фишера Fф определяется по формуле (1.12) как отношение объясненной суммы квадратов в расчете на одну независимую переменную к остаточной сумме квадратов в расчете на одну степень свободы:
 .
.
В нашем случае df1 = m =2, df2 = n - m – 1 = 16 – 2 – 1. Поэтому получаем:
 .
.
При уровне значимости 0,05 и df1 = 2, df2 =13 табличное значение Fт = 3,81. Неравенство Fт < Fф выполняется, гипотеза H0: α1 = α2 =0 отклоняется и признается статистическая значимость уравнения регрессии.
2.3. Проверим полученные результаты с помощью Пакет анализа Microsoft Excel. Зададим необходимые параметров в окне «Регрессия» Пакета анализа, см. рисунок 2.1.
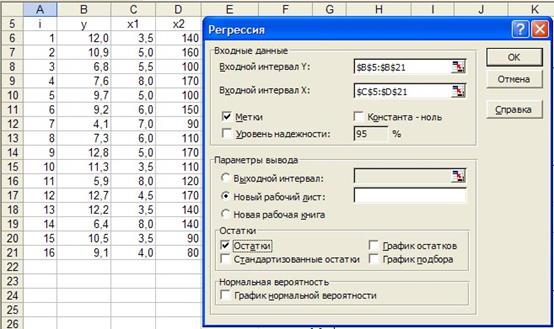
Рисунок 2.1 - Задание параметров раздела «Регрессия» Пакета анализа
Таблица 2.1 регрессионной статистики подтверждает правильность найденных коэффициентов детерминации R2 и множественной корреляции R.
Таблица 2.1 - Регрессионная статистика
| Множественный R | 0,97 |
| R-квадрат | 0,94 |
| Нормированный R-квадрат | 0,93 |
| Стандартная ошибка | 0,69 |
| Наблюдения |
В таблице 2.2 дисперсионного анализа, как и в п.2.2, получено: Fф =106,4.
Таблица 2.2 - Дисперсионный анализ
| df | SS | MS | F | Значимость F | |
| Регрессия | 101,57 | 50,78 | 106,4 | 0,000 | |
| Остаток | 6,20 | 0,48 | |||
| Итого | 107,77 |
Это подтверждает правильность отклонения гипотезы H0: α1 = α2 =0 и статистическую значимость уравнения регрессии. Напомним, что технология расчетов всех чисел в таблице 2.2 пояснена ранее в п. 1.3.
В таблице 2.3 показаны оценки коэффициентов регрессии и их статистики, полученные с помощью Пакета анализа Microsoft Excel.
Столбец «коэффициенты» убеждает нас в правильности уравнения регрессии (2.5), полученного «вручную» по формуле (2.3).
Таблица 2.3 - Коэффициенты
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 10,5 | 0,879 | 12,0 | 8,65 | 12,45 | |
| x1 | -1,42 | 0,109 | -13,0 | -1,66 | -1,18 | |
| x2 | 0,050 | 0,00578 | 8,65 | 0,0375 | 0,0623 |
Стандартные ошибки в столбце 3, определяющие доверительные интервалы коэффициентов и необходимые для расчета t -статистик, для множественной регрессии рассчитываются несколько иначе, чем для парной:
 , j=0,1,…m.
, j=0,1,…m.
Здесь zjj – диагональные элементы обратной матрицы  , полученные в выражении (2.4). Например, стандартна ошибка a0, как и в таблице 2.3, равна:
, полученные в выражении (2.4). Например, стандартна ошибка a0, как и в таблице 2.3, равна:
 .
.
Анализ t -статистик Стьюдента позволяет отвергнуть нулевые гипотезы H0: α0 =0, H0: α1 =0 H0: α2 =0 для каждого параметра в пользу альтернативной гипотезы. Таким образом, все параметры значимы, и их необходимо включать в модель.
2.4. Под точечным прогнозом среднего значения цены новой партии автомобилей понимается значение  , где
, где  -вектор независимых переменных, для которого определяется прогноз. В нашем случае
-вектор независимых переменных, для которого определяется прогноз. В нашем случае 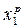 = 3 года - это возраст автомобиля.
= 3 года - это возраст автомобиля.  =165 л.с. - мощность двигателя.
=165 л.с. - мощность двигателя.
Под интервальным прогнозом среднего значения цены автомобилей понимается доверительный интервал цены, который находится по формуле
 , (2.6)
, (2.6)
где
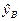 ,
,  - соответственно верхняя и нижняя границы доверительного интервала,
- соответственно верхняя и нижняя границы доверительного интервала,
 -вектор независимых переменных, для которого определяется интервал,
-вектор независимых переменных, для которого определяется интервал,
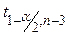 - квантиль распределения Стьюдента, (1 -a) - доверительная вероятность, n - количество наблюдений, (n- 3) - число степеней свободы,
- квантиль распределения Стьюдента, (1 -a) - доверительная вероятность, n - количество наблюдений, (n- 3) - число степеней свободы,
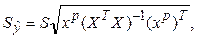
 ,
,
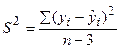 ,
,  , i=1,…,n.
, i=1,…,n.
Нахождение интервальных и точечных прогнозов по уравнению множественной регрессии проводится по следующей схеме.
Определяем вектор независимых переменных  , для которого необходимо получить прогноз. В соответствии с условием задачи
, для которого необходимо получить прогноз. В соответствии с условием задачи  .
.
Находим точечный прогноз:

Для нахождения интервального прогноза вычислим значения всех параметров, входящих в формулу (2.6)

 .
.
 ,
, 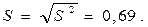
Тогда  .
.
Пусть 1- a =0,9. Тогда  = t 0,95;13 = 1,771. Поэтому:
= t 0,95;13 = 1,771. Поэтому:
 .
.
Следовательно,
 ;
;  .
.
Результаты вычислений целесообразно оформить в виде таблицы 2.4:
Таблица 2.4 - Прогноз

| Точечный прогноз | 
| Интервальный прогноз | |

| 
| 
| ||
| (1; 3; 165) | 14,5 | 0,40 | 13,8 | 15,2 |
2.5. На основании проведенных расчетов и полученных статистических характеристик можно сделать определенные выводы относительно взаимосвязей между исследуемыми экономическими показателями. Рассмотрим вначале зависимость цены от возраста. Так как  =-0,78 и проверка значимости этого коэффициента показала его существенное отличие от нуля, то есть основания утверждать, что между переменными y и x1 существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии
=-0,78 и проверка значимости этого коэффициента показала его существенное отличие от нуля, то есть основания утверждать, что между переменными y и x1 существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии  .
.
Коэффициент a0 =16,1 в данном случае имеет экономический смысл. Он формально определяет цену при x1 =0, т.е. цену нового автомобиля.
Коэффициент a1 = -1,26 также имеет вполне определенный экономический смысл, поскольку характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста на 1 год следует ожидать уменьшения цены на 1,26 тыс. у.е.
Необходимо особо подчеркнуть, что слова «следует ожидать снижения (прироста)...» в предыдущем предложении нельзя заменить словами «снижение цены составит...», так как уравнение регрессии y от x1 представляет собой лишь некоторую оценку стохастической зависимости между y и x1. Это уравнение характеризует так называемое среднее значение цены в зависимости от возраста автомобиля. Слово «среднее» выражает здесь тот факт, что реальное значение цены yi, соответствующее некоторому реальному возрасту xi1, будет находиться в некоторой окрестности значения  .
.
Значимое значение  = 0,44 (см. п.1.2) свидетельствует о том, что между y и x2 существует достаточно тесная линейная зависимость. Экономический смысл коэффициента b1 в уравнении
= 0,44 (см. п.1.2) свидетельствует о том, что между y и x2 существует достаточно тесная линейная зависимость. Экономический смысл коэффициента b1 в уравнении  аналогичен смыслу коэффициента a1 в уравнении
аналогичен смыслу коэффициента a1 в уравнении  , т.е. b1 показывает, какого прироста цены следует ожидать при увеличении мощности двигателя на единицу – на 1 л.с.
, т.е. b1 показывает, какого прироста цены следует ожидать при увеличении мощности двигателя на единицу – на 1 л.с.
В результате исследования зависимости объема цены от двух факторов - возраста и мощности двигателя, получено уравнение множественной регрессии  .
.
Содержательный смысл найденных коэффициентов уравнения состоит в следующем. Величина a1 = -1,42 показывает, что при увеличении возраста на 1 год и фиксированной (неизменной) мощности двигателя следует ожидать снижения цены автомобиля на 1,42 тыс. у. е.
Коэффициент a2 =0,05 показывает, что при увеличении мощности двигателя на 1 л.с. и фиксированном возрасте следует ожидать увеличения цены на 0,05 тыс. у. е.
Сравнение результатов, полученных на основе анализа уравнений парной регрессии, с результатами, полученными на основе анализа уравнения множественной регрессии, может создать представление об их противоречивости, поскольку оценки параметров заметно различаются. Однако здесь нет противоречия. Действительно, исследуя зависимость 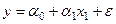 , мы исходим из того, что на цену влияет один единственный фактор – возраст автомобиля, а все остальные объясняющие факторы не учитывались (отбрасывались). Очевидно, что в реальности на цену влияет множество факторов: вес автомобиля, расход топлива, время разгона, регион производителя и т.д. Поэтому, рассматривая модель
, мы исходим из того, что на цену влияет один единственный фактор – возраст автомобиля, а все остальные объясняющие факторы не учитывались (отбрасывались). Очевидно, что в реальности на цену влияет множество факторов: вес автомобиля, расход топлива, время разгона, регион производителя и т.д. Поэтому, рассматривая модель 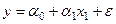 , мы фактически объединили все влияющие на y факторы в один результирующий и назвали этот фактор возрастом автомобиля. Точно такое же объединение всех факторов в один результирующий фактор было осуществлено при рассмотрении модели
, мы фактически объединили все влияющие на y факторы в один результирующий и назвали этот фактор возрастом автомобиля. Точно такое же объединение всех факторов в один результирующий фактор было осуществлено при рассмотрении модели 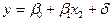 . Поэтому коэффициенты, отражающие степень (или силу) влияния каждого из двух рассмотренных факторов в отдельности на зависимую переменную, оказались достаточно большими.
. Поэтому коэффициенты, отражающие степень (или силу) влияния каждого из двух рассмотренных факторов в отдельности на зависимую переменную, оказались достаточно большими.
Для более точного описания изменения исследуемого показателя следует включать в эконометрическую модель по возможности большее количество объясняющих переменных (факторов). Вместе с тем, увеличение количества объясняющих факторов должно проводиться достаточно осторожно. С одной стороны, в числе этих факторов может оказаться такой, который не оказывает сколько-нибудь существенное влияние на объясняемую переменную y. С другой стороны, математическая модель может оказаться слишком громоздкой и неудобной для анализа. Существуют различные методы выявления и отбора существенных факторов. Простейший основан на вычислении и анализе коэффициентов парной корреляции  ,
,  ,...,
,..., 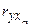 , где y - результирующий признак, а x1, x2,..., xm, - объясняющие факторы. Другой подход основан на рассмотренном дисперсионном анализе модели.
, где y - результирующий признак, а x1, x2,..., xm, - объясняющие факторы. Другой подход основан на рассмотренном дисперсионном анализе модели.
Следует помнить, что прежде, чем применять формальные, математические методы отбора и выявления существенных факторов, следует провести тщательный содержательный анализ изучаемого объекта или процесса.
Используемое в задачах 1 и 2 понятие доверительной вероятности характеризует степень уверенности в справедливости получаемого результата. Чем ближе к единице значение доверительной вероятности (1- a), тем с большей уверенностью можно утверждать, что прогнозируемое значение результирующего признака будет находиться в найденном доверительном интервале. Следует иметь в виду, что ширина доверительного интервала существенно зависит от значения (1- a): чем ближе к единице величина (1- a), тем шире доверительный интервал и, следовательно, хуже качество прогноза.
Очевидно, что достаточно широкий доверительный интервал прогноза не имеет никакого практического значения. Действительно, если мы получим результат типа:
«С вероятностью 0,999 среднее значение цены будет находиться в пределах от 0 до 20 тыс. у. е.», то от такого результата нет никакой практической пользы. При этом степень его достоверности оценивается в 99,9%. Поэтому при определении интервального прогноза приходится искать разумный компромисс между качеством прогноза, т.е. шириной доверительно интервала, и его достоверностью, т.е. значением доверительной вероятности.
| № | Название | Количество единиц в библиотеке |
| 1. | Кремер Н. Ш. Эконометрика: учеб. для вузов / Н. Ш. Кремер, Б. А. Путко; под ред. Кремера Н. Ш. - М.: ЮНИТИ-ДАНА, 2002. - 311с. | |
| Практикум по эконометрике: учеб. пособие для экон. вузов / Елисеева И. И., Курышева С. В., Гордеенко Н. М. и др.; под ред. Елисеевой И. И. - М.: Финансы и статистика, 2001. - 191с. | ||
| 3. | Домбровский В. В. Эконометрика: учебник / Федер. агентство по образованию, Нац. фонд подгот. кадров. - М.: Новый учеб., 2004. - 342с | |
| 4. | Эконометрика. Практикум / Сост. Иванова В.И., Кулагина А.Г., Ярдухин А.К. –– Чуваш. ун-т, Чебоксары, 2008. – 88 с | |
| 5. | Эконометрика: Метод. указания к контрольным заданиям / Сост. Никитин В.В., Кадышев Е.Н., Юсупов И.Ю. – Чуваш. ун-т, Чебоксары, 2004. – 64 с. |
Date: 2015-11-13; view: 896; Нарушение авторских прав