Основные определения, обозначения и используемые результаты

Приведем определения основных понятий, используемых в данной работе из источников [1] и[2]. Для введения понятия алгебы необходимо сначала определить -арные операции.

Определение 1.1. Если – непустое множество и , то -арной операцией на множестве назовем отображение прямого произведения 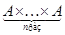в . Рассматриваются и -арные операции, которые по определению, отмечают некоторый элемент из .

Определение 1.2. Пара , где – непустое множество, а (возможно, пустое) множество операций на , называется универсальной алгеброй или, короче, алгеброй.

Совокупность операций (или опрерационных символов) будем называть сигнатурой. Часто, при введении алгебры, указывают только множество и не указывают сигнатуру.

Элемент алгебры отмечаемый -арной операцией . будем обозначать через .

Определение 1.3. Подмножество называется подалгеброй, если для всякой -арной операции ,

а если и – -арная операция из , то

Определение 1.4. Если , 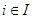– алгебры сигнатуры , то прямое произведение

становиться алгеброй той же сигнатуры, если для каждой -арной операции положить

а для -арной операции , где , –

Возникающая таким образом алгебра называется прямым произведением алгебр .

Приведем некоторые определения из

Определение 1.5. Отображение из алгебры в алгебру называется гомоморфизмом, если для любых элементов и любой -арной операции () справедливо равенство

Если же – нульарная операция, то полагаем

Взаимнооднозначный гомоморфизм алгебры на называется изоморфизмом и обозначается . Гомоморфизм алгебры в себя называется эндоморфизмом алгебры . Изоморфизм алгебры в себя называется ее автоморфизмом.

Определение 1.6. Конгруэнцией на алгебре называется всякая подалгебра прямого квадрата , обладающая следующими свойствами:

1) (рефлексивность): для всех ;

2) (симметричность): если 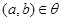, то ;

3) (транзитивность): если 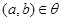и , то .

Отметим, что условия 1) – 3) означают, что – эквивалентностъ на множестве .

Определение 1.7. Пусть – гомоморфизм алгебры в . Ядром гомоморфизма называется подмножество

В работе [3] приводятся следующие теоремы об изоморфизмах

Теорема 1 Ядро гомоморфизма является конгруэнцией.

Определение 1.8. Если – конгруэнция на алгебре и , то множество

называется классом конгруэнции . Множество всех классов конгруэнции обозначают через . При этом для каждой -арной операции считают , а для -арной операции , где , – 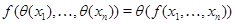. Получившуюся алгебру называют фактор-алгеброй алгебры по конгруэнции .

Теорема Первая теорема об изоморфизмах 2 Если – гомоморфизм алгебры в , то

Теорема Вторая теорема об изоморфизмах 3 Пусть конгруэнция на алгебре , – подалгебра алгебры . Тогда

Определение 1.9. Если , – конгруэнции на алгебре и содержится в , то обозначим

и назовем фактором алгебры или фактором на .

Теорема Третья теорема об изоморфизмах 4 Пусть – фактор на алгебре . Тогда

Определение 1.10. Если и – конгруэнции алгебры , то полагают

Теорема 5 Произведение двух конгруэнции является конгруэнцией тогда и только тогда, когда они перестановочны.

Определение 1.11. Класс алгебраических систем называется формацией, если выполняются следующие условия:

1) каждый гомоморфный образ любой -системы принадлежит ;

2) всякое конечное поддекартово произведение -систем принадлежит .

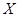Определение 1.12. Формальное выражение , где и – слова сигнатуры в счетном алфавите , называется тождеством сигнатуры . Скажем, что в алгебре выполнено тождество , если после замены букв любыми элементами алгебры и осуществления входящих в слова и операций слева и справа получается один и тот же элемент алгебры , т.е. для любых в алгебре имеет место равенство

Определение 1.13. Класс алгебр сигнатуры называется многообразием, если существует множество тождеств сигнатуры такое, что алгебра сигнатуры принадлежит классу тогда и только тогда, когда в ней выполняются все тождества из множества . Многообразие называется мальцевским, если оно состоит из алгебр, в которых все конгруэнции перестановочны.

Date: 2015-12-10; view: 288; Нарушение авторских прав