Критерий совместности системы. Ранг системы

Системы линейных уравнений.

Общая характеристика. Метод Гаусса решения систем.

Критерий совместности системы. Ранг системы.

Решение систем линейных уравнений – наиболее часто встречающаяся задача вычислительной математики в инженерной практике. К этой задаче сводятся или ею сопровождаются процедуры анализа и синтеза физических систем, химических процессов и составов различной природы: электрических, механических, гидравлических и т.п. Она играет важную роль во многих разделах современной науки и техники. Даже если исследуемая система нелинейна, то она сводится к решению систем линеаразованных уравнению и последующему их численному анализу.

Пусть дана система m линейных алгебраических уравнений с n неизвестными x ₁, x ₂,..., x _n и данными в правых частях свободными членами b ₁, b ₂, …, b _m:

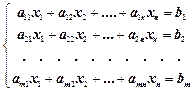(1).

В матричной форме эта система имеет вид: A· = , где =(x ₁, x ₂,..., x _n), =(b ₁, b ₂, …, b _m) – столбцы и A=A_mхn=(a _ij) - матрица коэффициентов, называемая основной матрицей системы (1).

Если ≠ , то системы (1) называется неоднородной, в противном случае, когда b ₁= b ₂=…= b _m=0, называется однородной.

Решением системы (1) называется совокупность n значений неизвестных х ₁= α ₁, х ₂= α ₂, …, x _n= α _n то есть вектор (x ₁, x ₂,..., x _n)=(α ₁, α ₂, …, α _n), при подстановке которых в систему все уравнения обращаются в верные равенства (тождества).

Система, имеющая хотя бы одно решение, называется совместной, не имеющая ни одного решения – несовместной. Система, имеющая единственное решение, называется определенной, имеющая более одного решения – неопределенной.

Две системы линейных уравнений относительно одних и тех же неизвестных называются эквивалентными, если каждое решение одной системы является решением другой системы или обе они несовместны.

Общий способ решения систем может быть основан на последовательном преобразовании системы (1) к такой эквивалентной системе, для которой решение находится достаточно просто. Мы опишем сейчас один из этих способов, называемый методом последовательного исключения неизвестных или методом Гаусса, который уже использовался для вычисления определителей и обращения матриц.

Применение вычислительных машин позволяет решать системы уравнений с большим числом неизвестных. Для этой цели разработаны высокоэффективные алгоритмы и программы.

Преобразования, которые оставляют множество решений системы (1) неизменным, то есть приводят к эквивалентной системе, следующие:

1) перестановка местами любых двух уравнений системы;

2) умножение, какого – либо из уравнений системы на число R ≠0;

3) прибавление, к какому – либо уравнению другого уравнения, умноженного на произвольное постоянное число.

Указанные три преобразования системы являются элементарными преобразованиями над строками расширенной матрицы системы (А │ В), где к основной матрице А добавлен через черту вектор–столбец свободных членов. Всегда можно, применяя подходящим образом элементарные операции над системой уравнений (1) или, что все равно, над расширенной матрицей (А │ В) добиться либо решения заданной системы, либо прийти к явно противоречивой системе в процессе решения.

Предположим, что среди коэффициентов в левых частях уравнений есть отличные от нуля. Поменяв, если нужно, некоторые из уравнений местами и перенумеровав неизвестные (переставив столбцы), можно добиться того, чтобы коэффициент а ₁₁ был не равен нулю. Прибавим теперь первое уравнение (строку матрицы), умноженное на , ко второму уравнению (строке), затем, умноженное на 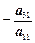, к третьему, умноженное на , - к m –ому уравнению, исключим неизвестное х ₁, из остальных m –1 уравнений. При проведении преобразований в случае получения уравнения вида 0· x ₁+0· x ₂+...+0· x _n=0, которое справедливо при любых значениях x ₁, x ₂,..., x _n, мы его исключаем из системы. Если же уравнение примет вид 0· x ₁+0· x ₂+0· x _n= γ, где γ ≠0, то, очевидно, оно не выполняется ни для каких значений x ₁, x ₂,..., x _n, и система уравнений, соответственно, не имеет решения.

Идея последовательного исключения неизвестных нашла свое воплощение в алгоритме Гаусса. Он сводится к преобразованию коэффициентов к нулю последовательно в каждом столбце расширенной матрицы (А │ В) ниже главной диагонали и приведению ее к эквивалентной матрице в форме верхней треугольной или ступенчатой:

~

~

Из последней матрицы, эквивалентной первоначальной, легко находится ранг r ₀ (число ненулевых строк) основной матрицы r ₀= r (A)= r (U) и ранг r _p расширенной матрицы r _p= = r (A│ )= r (U│ ).

Это позволяет дать простое и эффективное условие (критерий) совместности системы линейных уравнений (1).

Теорема 1. (Кронекер и Капелли). Система (1) имеет хотя бы одно решение (совместна) в том и только в том случае, когда ранг основной матрицы системы равен рангу расширенной: r ₀= r _p.

В случае их совпадения число r = r ₀= r _p называется рангомсистемы (1); он показывает количество линейно независимых уравнений в системе (1).

Для доказательства перепишем систему (1), пользуясь определением операций со столбцами. Мы получим:

(3).

1) Если существует решение (x ₁, x ₂,..., x _n), то запись (3) означает, что столбец членов есть линейная комбинация столбцов матрицы системы. Значит, добавление этого столбца не увеличивает общего числа линейно независимых столбцов и r (A│ )= r (A), r _p= r ₀= r.

2) Допустим теперь, что матрицы А и (А│ ) имеют одинаковый ранг r, и покажем, что система (1) совместна. Рассмотрим r базисных линейно независимых столбцов матрицы А; они будут базисными столбцами и расширенной матрицы (A│ ). Тогда все остальные столбцы, включая последний , матрицы (A│ ) есть линейная комбинация r базисных столбцов. Следовательно, столбец есть линейная комбинация всех столбцов матрицы А. Если мы коэффициенты этой последней комбинации обозначим через α ₁, α ₂, …, α _n, то получим, что выполняются равенства

.

Таким образом, система (1) удовлетворяется значениями x ₁= α ₁, x ₂= α ₂,..., x _n= α _n и, значит, совместна.

Пример 1. Выяснить совместимость систем:

а) , б) .

а) выпишем расширенную матрицу системы и приведем ее элементарными преобразованиями к треугольному виду (прямойход алгоритма Гаусса):

= .

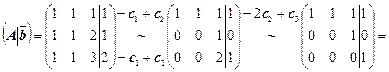
Ранг основной матрицы r ₀= r (A)= r (U)=2, ранг расширенной r _p= r (A│ )= r (U│ )=3. Так как r _p< r ₀, то система не имеет решения.

По–другому, если записать уравнением последнюю строку преобразованной матрицы 0· x ₁, 0· x ₂,..., 0· x _n=1, то в ней свободный член равен единице, а коэффициенты при неизвестных равны нулю, поэтому система несовместна.

б). Имеем прямой ход:

Ранг основной матрицы r ₀= r (A)= r (U)=2 равен рангу расширенной r _p= r (A│ )= r (U│ )=2, значит, система совместна и ранг системы r =2.

Получим решение системы (обратный ход алгоритма Гаусса). Из последней строки матрицы (U│ ) находим 0· х ₁=0· х ₂+1· х ₃=0, х ₃=0. Распишем первую строку х ₁+ х ₂+ х ₃=1 и подставим в нее значение х ₃=0, получим х ₁+ х ₂=1. Полагая х ₁= α - любое число (-∞< α <+∞), находим х ₂=1- α. Отсюда система имеет бесчисленное множество решений (х ₁, х ₂, х ₃)=(α, 1- α, 0), где α - произвольное число. Подставив в уравнение найденные значения неизвестных, можно убедиться в этом.

Рассмотрим другой подход. Пусть системе (1) отвечает линейное отображение = А n -мерного векторного пространства X ⁿ в m –мерное векторное пространство Y ^m с матрицей А относительно данных базисов. Отображение А ставит в соответствие пространству X ⁿ подпространство образов A (X ⁿ)Ì Y ^m, размерность которого равна рангу матрицы А, dimA (X ⁿ)= r (A)= r. Таким образом, нужно найти вектор Î Х ⁿ такой, что A = где Î Y ^m – данный вектор, отвечающий вектору из арифметического пространства A^m.

1. Если Ï А (X ⁿ), что возможно при r < m, то решения не существует.

2. Если Î A (X ⁿ), то возможны только два варианта:

1) если r = n (совпадает с числом неизвестных n), то отображение А взаимно однозначно и решение единственно: = A ^-1 , в матричной форме: =A^-1· ;

2) если r < n, то нужно рассмотреть (n – r) – мерное ядро – подпространство H Ì X ⁿ отображаемое А в нуль вектор; тогда существует бесконечно много решений вида + , где – одно из решений, а – произвольный вектор подпространства Н (A ( + )= A + A = + = ).

Date: 2015-12-10; view: 357; Нарушение авторских прав