Анализ состояния атмосферы с помощью термодинамических графиков

Аэрологическая диаграмма (см. рис. 4.4) позволяет достаточно быстро и с нуж­ной для практики точностью проводить анализ результатов зондирования атмосфе­ры. Рассмотрим некоторые из приемов такого анализа.

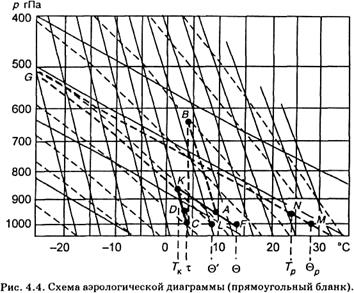
Характеристики влажности воздуха. На аэрологической диаграмме проведены изолинии доли насыщенного пара (s_m). Поэтому доля пара, отсчитанная в точке A, которая наносится по измеренным значениям температуры Т и давления р, будет представлять собой долю насыщенного пара для исходного состояния A (s_mA). Чтобы определить фактическую долю пара s_A, сместимся от точки A вдоль изобары до точки D, которая нанесена по известным (измеренным) значениям точки росы τ и давления р. Если теперь отсчитать значение доли пара по изогамме, проходящей через точ­ку D, то оно и будет представлять собой фактическую долю пара воздуха: s_mD = s_A. Относительная влажность определяется по соотношению f = (s_mD/s_mA) ∙ 100.

Уровень конденсации и кривая состояния влажной частицы. Через исходную точку А проведем сухую адиабату до пересечения с изогаммой, проходящей через точку D. Точка К — уровень конденсации. Выше точки К воздушная частица подни­мается влажноадиабатически. Таким образом, кривая AKG представляет собой кри­вую состояния влажной частицы, расположенной в начальный момент в точке A. Она всегда состоит из отрезков сухой и влажной адиабаты. В том частном случае, когда в начальный момент f = 100 %, кривая состояния представляет собой влажную адиа­бату.

Потенциальная температура Θ. От исходной точки А сместимся вдоль сухой адиабаты до изобары 1000 гПа (точка F), где и отсчитываем потенциальную темпера­туру.

Псевдоэквивалентная и псевдопотенциальная температуры. Наряду с поняти­ем влажноадиабатического процесса, который характеризуется тем, что вся сконденсировавшаяся при подъеме влага остается внутри воздушной частицы, введем понятие псевдоадиабатического процесса. Псевдоадиабатическим называется адиабатический процесс, протекающий во влажном насыщенном воздухе, при условии полно­го выпадения из частицы всей жидкой влаги. Если вся сконденсировавшаяся влага остается внутри воздушной частицы, то выше уровня конденсации кривой состояния частицы будет служить влажная адиабата; если сконденсировавшаяся влага целиком выпадает, то кривая состояния частицы — псевдоадиабата.

Из качественных физических представлений и теории (масса капель воды мала по сравнению с массой воздуха) вытекает, что различие между влажной адиабатой и псевдоадиабатой несущественно. Это означает, что практически псевдоадиабатиче­ский подъем частицы может быть заменен влажноадиабатическим. Однако наблюда­ется принципиальное различие в опускании воздушных частиц, поднявшихся до не­которого уровня влажно- и псевдоадиабатически. Влажноадиабатический процесс обратим: кривой состояния частицы при подъеме и опускании служит одна и та же влажная адиабата. Псевдоадиабатический процесс необратим: кривой состояния час­тицы при подъеме служит псевдоадиабата, а при опускании — сухая адиабата, в ре­зультате чего температура частицы после возвращения на исходный уровень оказы­вается выше, чем она была до подъема.

Псевдоэквивалентной температурой Т_р влажной частицы называется такая температура, которую принимает эта частица, если ее поднять сухоадиабатически до уровня конденсации, псевдоадиабатически до полной конденсации водяного пара (практически до того уровня, где сухая и влажная адиабаты пойдут параллельно), а затем опустить сухоадиабатически до исходного уровня (точка N).

Псевдопотенциальной температурой Θ_p называется такая температура, кото­рую принимает частица воздуха, если ее после псевдоадиабатического подъема до полной конденсации водяного пара опустить сухоадиабатически до уровня 1000 гПа (точка М).

При адиабатических процессах в сухом или влажном ненасыщенном воздухе, как уже отмечалось, сохраняет постоянное значение потенциальная температура 0. Действительно, на каком бы уровне ни находилась частица между точками A и К (см. рис. 4.4), ее потенциальная температура постоянна. Однако если частица дости­гает состояния насыщения и поднимается выше уровня конденсации, то, как это сле­дует из рис. 4.4, потенциальная температура этой частицы начинает возрастать. Это означает, что потенциальная температура уже не может служить консервативной ха­рактеристикой воздушной массы, если имеет место конденсация. В то же время, со­гласно рис. 4.4, где бы ни находилась влажная частица, если перемещение ее проис­ходит адиабатически, псевдопотенциальная температура этой частицы сохраня­ет постоянное значение.

Таким образом, псевдопотенциальная температура представляет собой консерва­тивную характеристику как сухоадиабатического, так и псевдоадиабатического (практически и влажноадиабатического) процесса. Изменение же Θ_p служит количе­ственным критерием неадиабатических воздействий (притока тепла) на воздушную массу. Эти свойства консервативности потенциальной и псевдопотенциальной темпе­ратур широко используются в так называемом изоэнтропическом анализе.

Не останавливаясь на выводе точной формулы, получим приближенную формулу для вычисления Т_р, которой можно пользоваться на практике. Температура частицы в точке N (см. рис. 4.4) оказалась выше температуры частицы в исходном положении благодаря теплоте, выделившейся при конденсации водяного пара. Представим Т_р в виде суммы: Т_р =Т + ∆Т_р, где ∆Т_р — эквивалентный добавок. В результате псевдо­адиабатического процесса сконденсировалась масса водяного пара, равная s. При этом выделилось количество тепла, равное Ls. Температура частицы повысилась при этом на ∆Т_р. Отсюда Ls ≈ c_p∆Т_р или ∆Т_р = Ls/c_p. Поскольку L = 2,5 10 ∙ Дж/кг, с_р ≈ 10³ Дж/(кг ∙ К), то ∆Т_р = 2,5s, Т_р =Т + 2,5s, причем здесь s — в промилле. Зная Т_р, нетрудно рассчитать псевдопотенциальную температуру по формуле

Такой же консервативной характеристикой, как и Θ_p, является потенциальная

температура смоченного термометра Θ′. Это температура, которую принимает влажная частица, если ее опустить влажноадиабатически с уровня конденсации z_к до уровня р = 1000 гПа (точка L на рис. 4.4).

Энергия неустойчивости. По данным температурного зондирования атмосферы (с помощью радиозонда, самолета, ракеты) на аэрологическую диаграмму наносится кривая стратификации атмосферы над данным пунктом. Для каждого подъема кро­ме кривой стратификации строится кривая состояния. Как правило, кривые страти­фикации и состояния не совпадают. Вследствие этого температура и плотность адиа­батически поднимающейся частицы на каждом уровне будут отличаться от темпера­туры и плотности атмосферы (T_i ≠ T_e,ρ_i ≠ ρ_е).

На каждом уровне на частицу, плотность которой отлична от плотности окружа­ющей среды, действует сила плавучести. Работа, которую совершает эта сила при вертикальном смещении частицы единичной массы на элементарное расстояние dz, согласно (4.5.1), равна

Воспользовавшись уравнением статики, перепишем формулу (4.11.1) в следую­щем виде:

На аэрологической диаграмме

Поэтому формулу (4.11.2) перепишем в виде

где В — некоторая постоянная.

Работа, совершенная силой плавучести при конечном перемещении частицы от уровня y₁(p₁) до уровня y₂(p₂) равна

Работа E_i, совершаемая силой плавучести при адиабатическом подъеме единич­ной массы воздуха от нижней границы данного слоя до верхней, носит название энер­гии неустойчивости этого слоя.

Произведение (T_i - Т_е)dy представляет собой на аэрологической диаграмме эле­ментарную площадь, заключенную между кривыми состояния T_i и стратификации Т_е, с одной стороны, и между двумя изобарами у и у + dy, с другой. Однако формула (4.11.3) показывает, что коэффициент пропорциональности между приращением энергии неустойчивости dE_i и площадью (T_i - Т_е)dy зависит от давления (ординаты). Поэтому на аэрологической диаграмме построена дополнительная шкала, позволяю­щая определять по небольшим площадкам, на которые разбивается общая площадь (заключенная между кривыми T_i и Т_е), энергию неустойчивости. На этой шкале нане­сены значения энергии неустойчивости, соответствующие (при фиксированном дав­лении) единичной площади аэрологической диаграммы. В согласии с формулой (4.11.3) чем меньше давление, тем больше энергия неустойчивости, отвечающая еди­ничной площади.

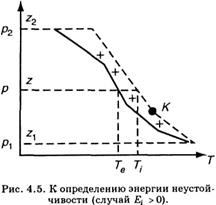
В отношении знака энергии неу­стойчивости возможны три различных случая.

1. Кривая состояния на всех уров­нях лежит правее кривой стратифика­ции (рис. 4.5). Тогда на всех уровнях Т_i > Т_е и, согласно (4.11.4), E_i > 0, т. е. энергия неустойчивости положитель­ная. При этом в нижних слоях атмосфе­ры стратификация, как правило, неу­стойчивая (γ > γ_а), а в более высоких слоях — может быть устойчивой. Боль­шая энергия неустойчивости способствует развитию в атмосфере мощных конвективных движений, приводящих к образованию кучевых и кучево-дождевых облаков. Такие условия в атмосфе­ре создаются летом в дневные часы.

2. Кривая состояния на всех уров­нях лежит левее кривой стратификации. Тогда на любом уровне T_i < Т_е и, согласно (4.11.4), E_i < 0, т. е. энергия неустойчивости отрицательная. В этом случае переме­щение частицы по вертикали вверх затруднено или полностью исключено, конвек­тивные движения воздуха при этом не наблюдаются.

3. Кривая состояния располагается справа от кривой стратификации в одних слоях и слева — в других. В этом случае энергия неустойчивости положительна в первых слоях и отрицательная во вторых. Общий запас энергии неустойчивости на­ходится как алгебраическая сумма энергий неустойчивости отдельных слоев.

Date: 2015-12-10; view: 2165; Нарушение авторских прав