Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Треугольник и все полученные линии построить в системе координат
|
|
Решение. 1) Расстояние между точками 
и 
определяется по формуле
(1)
воспользовавшись которой находим длину стороны 
:
. 
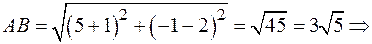
2) Уравнение прямой, проходящей через две заданные точки плоскости и ,имеет вид
(2)
Подставляя в (2) координаты точек 
и 
, получаем уравнение стороны :
.
Угловой коэффициент 
прямой найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом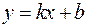 
.
У нас 
, то есть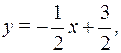 
откуда 
.
Аналогично получим уравнение прямой 
и найдем ее угловой коэффициент:
.
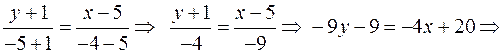
Далее
т.е.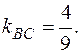 
3) Для нахождения внутреннего угла нашего треугольника воспользуемся формулой:
(3)
Отметим, что порядок вычисления разности угловых коэффициентов, стоящих в числителе этой дроби, зависит от взаимного расположения прямых и . Подумайте, как бы Вы стали искать внутренние углы и 
треугольника 
?
Подставив ранее вычисленные значения и 
в (3), находим
Теперь, воспользовавшись таблицами В.М. Брадиса или инженерным микрокалькулятором, получаем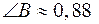 
рад.
4) Для составления уравнения медианы 
найдем сначала координаты точки 
, которая лежит на середине отрезка :
Подставив в уравнение (2)координаты точек и , получаем уравнение медианы:
.
5) Для составления уравнения высоты 
воспользуемся уравнением прямой, проходящей через заданную точку 
с заданным угловым коэффициентом 
, которое имеет вид
(4)
и условием перпендикулярности прямых и , которое выражается соотношением 
, откуда 
Подставив в (4) вместо значение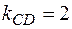 
, а вместо 
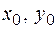соответствующие координаты точки , получим уравнение высоты :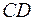
.
Для вычисления длины высоты 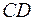воспользуемся формулой отыскания расстояния 
от заданной точки до заданной прямой с уравнением 
, которая имеет вид
(5)
Подставив в (5)вместо 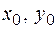координаты точки , а вместо 
коэффициенты уравнения прямой , получаем
.
6) Так как искомая прямая 
параллельна прямой , то 
. Подставив в уравнение (4) вместо 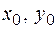координаты точки , а вместо значение 
, получаем уравнение прямой :
.
Для отыскания координат точки 
решаем совместно уравнения прямых и :
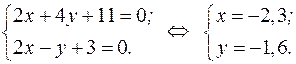
Таким образом,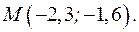 
7. Поскольку окружность имеет центр в точке 
и проходит через вершину 
, то по формуле (1) ее радиус
Каноническое уравнение окружности радиуса 
с центром в точке имеет вид
(6)
В нашем примере искомое уравнение выглядит следующим образом:
Треугольник , высота 
, медиана , прямая , точка и окружность построены в системе координат 
на рис. 1.
ПРИМЕРНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ
1. Понятие матрицы. Действия над матрицами: умножение матриц на число, сложение и умножение матриц. Транспонирование матриц.
2. Ранг матрицы. Вычисление ранга матрицы.
3. Определители n-го порядка, их свойства и вычисление.
4. Алгебраические дополнения и миноры.
5. Определители второго и третьего порядков, их свойства и вычисление.
6. Обратная матрица. Способы отыскания обратной матрицы.
7. Понятие системы линейных уравнений (СЛУ). Совместность и определённость СЛУ.
8. Решение систем линейных уравнений матричным способом.
9. Решение систем линейных уравнений по формулам Крамера.
10. Решение систем линейных уравнений методом Гаусса.
11. Базис. Система координат. Линейные операции над векторами в координатах.
12. Векторное и смешанное произведение векторов.
13. Уравнение линии на плоскости.
Date: 2015-12-10; view: 303; Нарушение авторских прав