Примеры решения задач

Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct ³, где A =4 м, B =2 м/с, С =-0,5 м/с³. Для момента времени t ₁=2 с определить:

1) координату x ₁ точки, 2) мгновенную скорость v ₁, 3) мгновенное ускорение a₁.

Решение. 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения вместо t заданное значение времени t ₁:

x=A+Bt+Ct³.

Подставим в это выражение значения A, В, С, t ₁ и произведем вычисления:

x ₁=(4+4 - 0,5· 2³) м=4 м.

2. Мгновенную скорость в произвольный момент времени найдем, продифференцировав координату х по времени:

Тогда в заданный момент времени t ₁ мгновенная скорость v ₁=B+3C t ₁².

Подставим сюда значения В, С, t ₁ и произведем вычисления: v ₁ =- 4 м/с.

Знак минус указывает на то, что в момент времени t₁=2 с точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты х по времени:

Мгновенное ускорение в заданный момент времени t ₁ равно a ₁ =6Ct ₁. Подставим значения С, t ₁и произведем вычисления:

a ₁=(-6 ·0,5· 2) м/с= - 6 м/с.

Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

Пример 2. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R= 50 м. Уравнение движения автомобиля S (t) = A+Bt+Ct², где A=10 м, B=10 м/с, С= – 0,5 м/с². Найти: 1) скорость v автомобиля, его тангенциальное 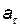, нормальное а _n. и полное а ускорения в момент времени t =5 с; 2) длину пути l и модуль перемещения | | автомобиля за интервал времени =10 с, отсчитанный с момента начала движения.

Решение. 1. Зная уравнение движения, найдем скорость, взяв первую производную от координаты по времени:

.

Подставим в это выражение значения В, С, t и произведем вычисления:

v =5 м/с.

Тангенциальное ускорение найдем, взяв первую производную от скорости по времени: Подставив значение С, получим 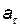= ‑ 1 м/с².

Нормальное ускорение определяется по формуле . Подставим сюда найденное значение скорости и заданное значение радиуса кривизны траектории и произведем вычисления:

a_n =0,5 м/с².

Полное ускорение является геометрической суммой ускорени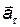й и 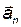: . Модуль ускорения . Подставив в это выражение найденные значения а и а _n получим

а =1,12 м/с².

2. Чтобы определить путь l, пройденный автомобилем, заметим, что в случае движения в одном направлении (как это имеет место в условиях данной задачи) длина пути l равна изменению криволинейной координаты 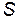т. е.

l = , или .

Подставим в полученное выражение значения В, С, и произведем вычисления:

l =50 м.

Модуль перемещения, как это видно из рис. 1, равен | |=2Rsin( /2),

Подставим сюда значения R, l ипроизведем вычисления:

| |= 47,9м.

Пример 3. Маховик, вращавшийся с постоянной частотой ₀=10 с^-1, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой = 6 с^-1. Определить угловое ускорение маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N =50 оборотов.

Решение. Угловое ускорение маховика связано с начальной и конечной угловыми скоростями соотношением 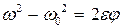, откуда Но так как 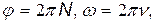то

Подставив значения , , ₀, N и вычислив, получим:

=3,14(6²-10²)/50 рад/с²= – 4,02 рад/с².

Знак минус указывает на то, что маховик вращался замедленно. Определим продолжительность торможения, используя формулу, связывающую угол поворота со средней угловой скоростью вращения и временем t: . По условиям задачи, угловая скорость линейно зависит от времени и поэтому можно написать , тогда ,

Откуда: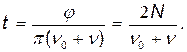

Подставив числовые значения и произведя вычисления, получим

Пример 4. К концам однородного стержня приложены две противоположно направленные силы: F ₁=40H и F ₂=100 H (рис. 2, a).

Определить силу натяжения Т стержня в поперечном сечении, которое делит стержень на две части в отношении 1: 2.

Решение. Если бы силы F ₁и F ₂ были равны между собой, то сила натяжения в любом сечении стержня была бы одинаковой и равной силам, приложенным к концам стержня. Стержень в этом случае находился бы в покое. Но так как сумма сил, действующих на стержень, отлична от нуля, то стержень будет двигаться с ускорением, величина и направление которого определяются по второму закону Ньютона: , где т – масса стержня. Так как обе силы действуют вдоль прямой, то геометрическую сумму можно заменить алгебраической:

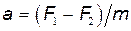. (1)

При ускоренном движении стержня силы натяжения в разных сечениях различны. Для определения этих сил применим следующий прием: разделим стержень на две части в интересующем нас сечении и отбросим одну из них, например левую. Действие левой части на правую заменим силой натяжения Т (рис. 2, б ). В результате действия разности сил F₂ – Т оставшаяся правая часть стержня массой m ₁ должна двигаться с ускорением равным по величине и направлению прежнему ускорению, выражаемому формулой (1). Так как стержень однородный, то m ₁ =m/ 3 и, следовательно,

. (2)

Приравнивая правые части равенства (1) и (2) и выражая из полученного равенства силу натяжения Т, находим

T=F ₂ – (F ₂ – F ₁) / 3.

Подставив значения F ₂ и F ₁, получим

Т =80 Н.

Пример 5. В лифте на пружинных весах находится тело массой т= 10 кг (рис. 3, а). Лифт движется с ускорением а =2 м/с². Определить показания весов в двух случаях, когда ускорение лифта направлено: 1) вертикально вверх, 2) вертикально вниз.

Решение. Определить показания весов — это значит найти вес тела G, т. е. силу, с которой тело действует на пружину. Но эта сила, по третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости N (силе реакции опоры), с которой пружина через посредство прикрепленной к ней чашки весов действует на тело, т. е.

или G=N. (1) Следовательно, задача определения показания весов сводится к нахождению реакции опоры N.

Задачу можно решать как в инерциальной, так и неинерциальной системе отсчета.

Решение в инерциальной системе отсчета. На тело действуют две силы: сила тяжести и сила .

Направим ось z вертикально вверх и спроецируем на нее все силы, действующие на тело. Индекс z у проекции сил опустим, так как проекции и сами силы совпадают по величине. Направление сил учтем знаком плюс или минус. Напишем уравнение движения:

, откуда . (2)

Из равенств (1) и (2) следует:

.

При вычислении показания весов следует учесть знак ускорения:

1) ускорение направлено вертикально вверх (a >0), тогда:

G ₁=10(9,81+2)H=118 Н;

2) ускорение направлено вертикально вниз (a <0), тогда

G ₂==10(9,81 – 2) Н=78 Н.

Отметим, что ни модуль, ни направление скорости лифта не влияют на показания весов. Существенны лишь величина и направление ускорения.

Решение в неинерциальной системе отсчета, т. е. в системе, движущейся ускоренно вместе с лифтом. В этой системе отсчета законы Ньютона не выполняются. Однако, если к телу в соответствии с принципом Даламбера дополнительно к действующим на него силам приложить силу инерции:

,

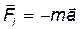где а — ускорение системы отсчета, то с учетом этой силы законы Ньютона будут справедливы.

В этом случае на тело будут действовать три силы: сила тяжести , сила упругости и сила инерции 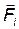; (рис. 3, б). Под действием этих сил тело в данной неинерциальной системе отсчета покоится. Это значит, что вместо уравнений динамики (законов Ньютона) можно воспользоваться законами статики. Если тело под действием системы сходящихся сил покоится, то геометрическая сумма этих сил равна нулю. В данном случае это приводит к равенству:

.

Спроецируем все силы на ось z и напишем соответствующее равенство для проекций этих сил (индекс z опустим):

N – P – ma= 0,

откуда сила реакции опоры:

N=P+ma=m (g+a). (3)

Из равенств (1) и (3) следует

G=m (g+a),

что совпадает с результатом, полученным при решении в инерциальной системе отсчета.

Пример 6. При падении тела с большой высоты его скорость v _уст установившемся движении достигает 80 м/с. Определить время , в течение которого, начиная от момента начала падения, скорость становится равной 1/2 v _уст. Силу сопротивления воздуха принять пропорциональной скорости тела.

Решение. На падающее тело действуют две силы (рис. 4, а):

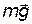сила тяжести и сила сопротивления воздуха .

Сила сопротивления воздуха по условиям задачи пропорциональна скорости тела и противоположна ей по направлению:

, (1)

где k — коэффициент пропорциональности, зависящий от размеров, формы тела и от свойств окружающей среды.

Напишем уравнение движения тела в соответствии со вторым законом Ньютона в векторной форме: . Заменив согласно (1), получим:

Спроецируем все векторные величины на вертикально направленную ось и напишем уравнение для проекций:

После разделения переменных получим:

.

Выполним интегрирование, учитывая, что при изменении времени от нуля до (искомое время) скорость возрастает от нуля до 1/2 v _уст (рис. 4, б):

Подставим пределы интегрирования в левую часть равенства:

и найдем из полученного выражения искомое время:

(2)

Входящий сюда коэффициент пропорциональности k определим из следующих соображений. При установившемся движении (скорость постоянна) алгебраическая сумма проекций (на ось y) сил, действующих на тело, равна нулю, т. е. mg–kv _уст = 0, откуда k=mg/v _уст. Подставим найденное значение k в формулу (2):

После сокращений и упрощений получим:

Проверка размерности в данном случае не обязательна, так как результат очевиден. Подставив в эту формулу значения v _уст, g, ln2 и произведя вычисления, получим:

=5,66 с.

Пример 7. Шар массой m =0,3 кг, двигаясь со скоростью v =10 м/с, упруго ударяется о гладкую неподвижную стенку так, что скорость его направлена под углом =30° к нормали. Определить импульс р, получаемый стенкой.

Решение. Сначала проанализируем условие задачи. Стенка неподвижна, поэтому система отсчета, связанная с ней, будет инерциальной. Удар о стенку упругий; следовательно, можно воспользоваться законом сохранения механической энергии. Из него, учитывая, что масса стенки много больше массы шара, следует равенство модулей скоростей шара | | до и | | после удара.

Покажем, что угол ' отражения шара от стенки равен углу падения шара. Спроецируем векторы и на координатные оси Ох и Оу (рис. 5). Так как стенка гладкая, то . Учитывая, кроме того, что | |=| |, получим а отсюда следует равенство углов падения и отражения ( '= ).

Для определения импульса, полученного стенкой, воспользуемся законом сохранения импульса. Для нашего случая этот закон можно записать в виде:

где – импульсы шара до и после удара . Отсюда импульс, полученный стенкой,

Из рис. 6 видно, что вектор сонаправлен с осью Ох и его модуль . Подставив сюда выражение импульса p ₁ =mv, получим

.

Произведем вычисления:

.

Пример 8. На спокойной воде пруда стоит лодка длиной L и массой М перпендикулярно берегу, обращенная к нему носом. На корме стоит человек массой т. На какое расстояние s приблизится лодка к берегу, если человек перейдет с кормы на нос лодки? Трением о воду и воздух пренебречь.

Решение. 1-й способ. Для простоты решения будем считать, что человек идет по лодке с постоянной скоростью. Лодка в этом случае также будет двигаться равномерно. Поэтому перемещение лодки относительно берега определим по формуле:

s= vt (1)

где v — скорость лодки относительно берега; t — время движения человека и лодки. Направление перемещения человека примем за положительное.

Скорость v лодки найдем, пользуясь законом сохранения импульса (количества движения). Так как, по условию задачи, система человек — лодка в начальный момент была относительно берега в покое, то по закону сохранения импульса получим Mv – mu =0, где и — скорость человека относительно берега; знак минус указывает на то, что скорости человека и лодки по направлению противоположны. Отсюда v=mu/M.

Время t движения лодки равно времени перемещения человека по лодке, т. е. t=s₁/u=(L—s)/u, где s₁ — перемещение человека относительно берега.

Подставив полученные выражения v и t в формулу (1), найдем:

откуда:

s=mL/ (m+M).

Заметим, что предположение о равномерности движения человека не является обязательным. В приведенном ниже более общем способе решения задачи такое предположение не используется.

2-й способ. Согласно следствию из закона сохранения импульса, внутренние силы системы тел не могут изменить положение центра инерции системы. Применяя это следствие к системе человек — лодка, можно считать, что при перемещении человека по лодке центр масс системы не изменит своего положения, т. е. останется на прежнем расстоянии от берега.

Пусть центр масс системы человек — лодка находится на вертикали, проходящей в начальный момент через точку C ₁ лодки (рис. 7), а после перемещения лодки — через другую ее точку С ₂. Так как эта вертикаль неподвижна относительно берега, то искомое перемещение s лодки относительно берега равно перемещению лодки относительно вертикали. А это последнее легко определить по перемещению центра масс О лодки. Как видно из рис. 7, в начальный момент точка О находится слева от вертикали на расстоянии a ₁, а после перехода человека — на расстоянии a ₂ справа от нее. Следовательно, искомое перемещение лодки s=a ₁ +a ₂. (2)

Для определения a ₁ и a ₂ воспользуемся тем, что относительно центра тяжести системы моменты сил тяжести лодки и человека должны быть равны. Для точки C ₁ имеем Mga₁=mg (l – a₁), где l — первоначальное расстояние человека от центра тяжести лодки. Отсюда получим а₁=тl/ (М+т). Для точки С ₂ имеем Mga₂=mg (L–a₂–l), откуда a₂=m (L–l) / (М+т).

Подставив выражения a ₁ и а ₂ в формулу (2), получим:

s=mL/ (M+m),

что совпадает с результатом, полученным первым способом.

Пример 9. Два шара массами m ₁=2,5 кг и m ₂=1,5 кг движутся навстречу друг другу со скоростями v ₁=6 м/с и v ₂ = 2 м/с. Определить: 1) скорость и шаров после удара; 2) кинетические энергии шаров W_{K 1} до и W_{K 2} после удара; 3) долю кинетической энергии шаров, превратившейся во внутреннюю энергию. Удар считать прямым, неупругим.

Решение. 1. Неупругие шары не восстанавливают после удара своей первоначальной формы. Следовательно, не возникают силы, отталкивающие шары друг от друга, и шары после удара будут двигаться совместно с одной и той же скоростью и. Определим эту скорость по закону сохранения импульса

,

где: ; – импульсы первого и второго шаров до удара; ; – импульсы первого и второго шаров после удара.

В проекции на направление движения первого шара до удара, закон сохранения импульса примет вид:

m₁v₁ – т₂v₂= (т₁ + m₂) и,

откуда:

u= (m₁v₁ – т₂v₂)/(т₁ + m₂).

u =(2,5· 6–1,5· 2)/(2,5+1,5) м/с=3 м/с.

2. Кинетические энергии шаров до и после удара определим по формулам:

W_{K 1} = m₁v₁²/2 + m₂v₂² / 2; W_K2 = (m₁ + т₂) u² / 2.

Произведя вычисления по этим формулам, получим:

W_{K 1}=(2,5·6²/2+1,5·2²/2) Дж=48 Дж;

W_{K 2} = (2,5+1,5) З²/2 Дж=18 Дж.

3. Сравнение кинетических энергий шаров до и после удара показывает, что в результате неупругого удара шаров произошло уменьшение их кинетической энергии, за счет чего увеличилась их внутренняя энергия. Долю кинетической энергии шаров, пошедшей на увеличение их внутренней энергии, определим из соотношения:

Пример 10. Шар массой m ₁, движущийся горизонтально с некоторой скоростью v₁, столкнулся с неподвижным шаром массой т ₂. Шары абсолютно упругие, удар прямой. Какую долю своей кинетической энергии первый шар передал второму?

Решение. Доля энергии, переданной первым шаром второму, выразится соотношением:

(1)

где — кинетическая энергия первого шара до удара; u ₂ и 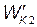, — скорость и кинетическая энергия второго шара после удара.

Как видно из выражения (1), для определения надо найти u ₂. Воспользуемся тем, что при ударе абсолютно упругих тел одновременно выполняются два закона сохранения: импульса и механической энергии.

По закону сохранения импульса, учитывая, что второй шар до удара покоился, имеем . По закону сохранения энергии в механике, Решая совместно два последних уравнения, найдем:

u ₂=2 m ₁ v ₁/(m ₁+ m ₂).

Подставив это выражение u ₂ в равенство (1), получим:

Из этого соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами.

Пример 11. Боек (ударная часть) свайного молота массой т ₁=500 кг падает на сваю массой m ₂=100 кг со скоростью v ₁=4 м/с. Определить: 1) кинетическую энергию бойка в момент удара; 2) энергию , затраченную на углубление сваи в грунт; 3) кинетическую энергию 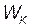, перешедшую во внутреннюю энергию системы; 4) КПД удара бойка о сваю. Удар бойка о сваю рассматривать как неупругий.

Решение. 1. Кинетическую энергию бойка в момент удара о сваю находим по формуле = m ₁ v ₁²/2. Подставив значения m ₁, и v ₁ и произведя вычисления, получим:

=(500×4²)/2 Дж=4000 Дж=4 кДж.

2. Чтобы определить энергию, затраченную на углубление сваи, предварительно найдем скорость системы боек — свая непосредственно после удара. Для этого применим закон сохранения импульса, который в случае неупругого удара выражается формулой:

т ₁ v ₁+ m ₂ v ₂=(m ₁+ m ₂) u, (1)

где v ₂ — скорость сваи перед ударом; и — скорость бойка и сваи непосредственно после удара. Свая перед ударом находилась в состоянии покоя, поэтому v ₂=0. Так как удар неупругий, то боек и свая после удара движутся как одно целое, т. е. с одинаковой скоростью и. Из формулы (1) найдем эту скорость:

(2)

В результате сопротивления грунта скорость бойка и сваи после удара быстро гасится, а кинетическая энергия, которой обладает система боек — свая, затрачивается на углубление сваи в грунт.

Эту энергию находим по формуле Заменим скорость и ее выражением (2): или, учитывая, что = m ₁ v ₁²/2, запишем:

(3)

Подставив в формулу (3) значения т ₁, m ₂ и и произведя вычисления, получим:

= [500/(500+100)]. 4·10³ Дж=3,33·10³ Дж=3,33 кДж.

3. Боек до удара обладал энергией ; — энергия, затраченная на углубление сваи в грунт. Следовательно, во внутреннюю энергию, связанную с неупругой деформацией сваи, превратилась энергия:

= — .

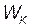Подставив в это выражение значения T ₁ и T ₂, найдем

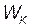=0,67 кДж.

4. Свайный молот служит для забивки сваи в грунт; следовательно, энергию следует считать полезной. КПД удара бойка о сваю выразится как отношение энергии , затраченной на углубление сваи в грунт, ко всей затраченной энергии :

= / .

Подставив в последнее выражение по формуле (3), получим

=m₁/(m₁+m₂).

Подставим значения m ₁ и т ₂и произведем вычисления:

=83,3%.

Пример 12. Вычислить момент инерции J_z молекулы NО₂ относительно оси z, проходящей через центр масс молекулы перпендикулярно плоскости, содержащей ядра атомов. Межъядерное расстояние d этой молекулы равно 0,118 нм, валентный угол =140°.

Решение. Молекулу NO₂ можно рассматривать как систему, состоящую из трех материальных точек общей массой

m =2 m ₁+ m ₂, (1)

где m ₁ — масса атома кислорода; m ₂ — масса атома азота.

Расположим молекулу относительно координатных осей так, как это указано на рис. 8 (начало координат совместим с центром масс С молекулы, ось z направим перпендикулярно плоскости чертежа «к нам».)

Для определения J_z воспользуемся теоремой Штейнера:

J=J _c+ ma ².

Для данного случая эта теорема запишется в виде J_z' = J_z+ma ², где J_z' — момент инерции относительно оси z', параллельной оси z и проходящей через атом азота (точка О на рис. 8). Отсюда искомый момент инерции

J_z = J_z' –ma ² (2)

Момент инерции J_z' находим как сумму моментов инерции двух материальных точек (атомов кислорода):

J_z' = 2m₁ d ² (3)

Расстояние а между осями z и z ' равно координате x_с центра масс системы и поэтому может быть выражено по формуле:

.

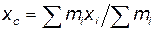В данном случае:

а = х _с= (2 m ₁ x ₁+ m ₂ x ₂)/(2 m ₁+ m ₂),

или, учитывая, что x ₁= d cos ( /2) и х ₂ = 0,

(4)

Подставив в формулу (2) значения J_z', т, а соответственно из выражений (3), (1), (4), получим:

или после преобразований:

(5)

Относительные атомные массы кислорода (A _O=16) и азота (А _N=14). Запишем массы атомов этих элементов в атомных единицах массы (а.е.м.), а затем выразим в килограммах (1 а.е.м. =1,66 ·10^-27 кг):

m ₁= 161,66·10^-27 кг=2,66·10^-26 кг;

m ₂ = 141,66·10^-27 кг = 2,32·10^-26 кг.

Значения m ₁, т ₂, d и подставим в формулу (5) и произведем вычисления:

J_z =6,80·10^-46 кг·м².

Пример 13. Физический маятник представляет собой стержень длиной l =1 м и массой m ₁=l кг с прикрепленным к одному из его концов диском массой т ₂ = 0,5 m ₁. Определить момент инерции J _zтакого маятника относительно оси Оz, проходящей через точку О на стержне перпендикулярно плоскости чертежа (рис. 9).

Решение. Общий момент инерции маятника равен сумме моментов инерции стержня J_z1 и диска J_z2.

J_z ⁼ J_z1 + J_z2 (1)

Формулы, по которым вычисляются моменты инерции стержня J_{z 1} и диска J_{z 2} относительно осей, проходящих через их центры масс, даны в табл. на с. 13. Чтобы определить моменты инерции J_{z 1} и J_{z 2}, надо воспользоваться теоремой Штейнера:

J=J_c+ma². (2)

Выразим момент инерции стержня согласно формуле (2):

J_z1=^l/₁₂m₁l²+m₁a₁².

Расстояние a ₁ между осью Оz и параллельной ей осью, проходящей через центр масс C ₁ стержня, как следует из рис. 9, равно ¹/₂ l ‑ ^l/₃ l= ^l/₆ l. С учетом этого запишем:

J_{z 1} = ^l/₁₂ m ₁ l ²+ m ₁ (^l/₆ l)²=¹/₉ m ₁ l ²=0,111 m ₁ l ².

Момент инерции диска в соответствии с формулой (2) равен:

J_{z 2}=^l/₂ m ₂ R ²+ m ₂ a ₂².

где R — радиус диска; R= ¹/₄ l. Расстояние а ₂ между осью Оz и параллельной ей осью, проходящей через центр масс диска, равно (рис. 9) ²/₃ l + ^l/₄ l= ^l1/₁₂ l. С учетом этого запишем:

J_{z 2}=^l/₂ m ₂ (¹/₄ l)²+ m ₂(^l1/₁₂ l)²= 0,0312 m ₂ l ² + 0,840 m ₂ l ²= 0,871 m ₂ l ².

Подставив полученные выражения J_z1 и J_z2 в формулу (1), найдем

J_z= 0,111 m ₁ l ²+0,871 m ₂ l ²=(0,111 m ₁+0,871 m ₂) l ²,

или, учитывая, что т ₂ = 0,5 m ₁,

J_z= 0,547 m ₁ l ².

Произведя вычисления, получим значение момента инерции физического маятника относительно оси Оz:

J_z =0,547·1·1 кг·м²=0,547 кг·м².

Пример 14. Вал в виде сплошного цилиндра массой m ₁ = 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m ₂=2 кг (рис. 10). С каким ускорением а будет опускаться гиря, если ее предоставить самой себе?

Решение. Линейное ускорение а гири равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности,

и связано с угловым ускорением вала соотношением:

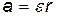, (1)

где r — радиус вала.

Угловое ускорение вала выражается основным уравнением динамики вращающегося тела:

, (2)

где М — вращающий момент, действующий на вал; J — момент инерции вала. Рассматриваем вал как однородный цилиндр. Тогда его момент инерции относительно геометрической оси равен

J= ¹/₂ m ₁ r ².

Вращающий момент М, действующий на вал, равен произведению силы натяжения Т шнура на радиус вала: М=Тr.

Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: сила тяжести , направленная вниз, и сила натяжения шнура, направленная вверх. Равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона, m ₂ g – T=m₂a, откуда T=m₂ (g – а). Таким образом, вращающий момент M=m ₂(g—а) r.

Подставив в формулу (2) полученные выражения М и J, найдем угловое ускорение вала:

Для определения линейного ускорения гири подставим это выражение в формулу (1). Получим

,

откуда

.

Пример 15. Через блок в виде диска, имеющий массу m =80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m ₁=100 г и m ₂=200 г (рис. 11). С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение. Применим к решению задачи основные законы поступательного и вращательного движения. На каждый из движущихся грузов действуют две силы: сила тяжести 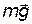, направленная вниз, и сила натяжения нити, направленная вверх.

Так как вектор ускорения 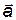груза m ₁ направлен вверх, то T ₁> m ₁ g. Равнодействующая этих сил вызывает равноускоренное движение и, по второму закону Ньютона, равна T ₁ – т ₁ g=т ₁ а, откуда:

T ₁ =m ₁ g+m ₁ a. (1)

Вектор ускорения 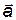груза т ₂ направлен вниз; следовательно, T ₂< m ₂ g. Запишем формулу второго закона для этого груза:

m ₂ g – T ₂ =m₂a, откуда

T ₂ =m₂g – m₂а. (2)

Согласно основному закону динамики вращательного движения, вращающий момент М, приложенный к диску,равен произведению момента инерции J диска на его угловое ускорение :

M=J . (3)

Определим вращающий момент. Силы натяжения нитей действуют не только на грузы, но и на диск. По третьему закону Ньютона, силы и 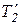, приложенные к ободу диска, равны соответственно силам T ₁ и Т ₂, но по направлению им противоположны. При движении грузов диск ускоренно вращается по часовой стрелке; следовательно, 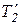> . Вращающий момент, приложенный к диску, равен произведению разности этих сил на плечо, равное радиусу диска, т. е. M =(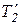 – ) r. Момент инерции диска J=mr ²/2, угловое ускорение связано с линейным ускорением грузов соотношением . Подставив в формулу (3) выражения М, J и , получим

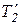( – ) r =

откуда

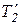– =(т /2) а.

Так как =T ₁ и 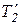= Т ₂, то можно заменить силы и 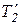вы­ражениями по формулам (1) и (2), тогда:

m₂g – m₂a – m₁g – m₁a= (m/2) a, или(m₂—m₁) g= (m₂+m₁+m /2) a

откуда:

(4)

Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому значения масс m ₁, m ₂ и m можно выразить в граммах, как они даны в условии задачи. После подстановки получим:

Пример 16. Маховик в виде диска массой m =50 кг и радиусом r =20 см был раскручен до частоты вращения ₁=480 мин^-1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t =50 с; 2) маховик до полной остановки сделал N= 200 оборотов.

Решение. 1.По второму закону динамики вращательного движения, изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента:

M t=J — J ,

где J — момент инерции маховика; и — начальная и конечная угловые скорости. Так как =0 и t = t, то Mt= – J , откуда:

M = – J /t. (1)

Момент инерции диска относительно его геометрической оси равен J=¹/₂mr². Подставив это выражение в формулу (1), найдем

M= – mr² / (2 t). (2)

Выразив угловую скорость через частоту вращения ₁ и произведя вычисления по формуле (2), найдем:

М= – 1 Н·м.

2. В условии задачи дано число оборотов, сделанных махови­ком до остановки, т. е. его угловое перемещение. Поэтому приме­ним формулу, выражающую связь работы с изменением кинетиче­ской энергии:

или, учтя, что ,

(3)

Работа при вращательном движении определяется по формуле A=Mj. Подставив выражения работы и момента инерции диска в формулу (3), получим:

M = – mr ² /4.

Отсюда момент силы трения:

М= – mr ² /4 . (4)

Угол поворота j= 2 N =2·3,14·200 рад=1256 рад. Произведя вычисления по формуле (4), получим:

М= – 1 Н·м.

Знак минус показывает, что момент силы трения оказывает тормозящее действие.

Пример 17. Платформа в виде диска радиусом R = 1,5 м и массой m ₁ = 180 кг вращается по инерции около вертикальной оси с часто­той =10 мин^-1. В центре платформы стоит человек массой т ₂=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение. По закону сохранения момента импульса,

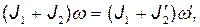(1)

где J ₁ — момент инерции платформы; J ₂ — момент инерции человека, стоящего в центре платформы; — угловая скорость платформы с человеком, стоящим в ее центре; J₂' — момент инерции человека, стоящего на краю платформы; — угловая скорость платформы с человеком, стоящим на ее краю.

Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением:

. (2)

Определив из уравнения (1) и подставив полученное выражение в формулу (2), будем иметь:

v= (J ₁ +J ₂) R /(J ₁ +J' ₂). (3)

Момент инерции платформы рассчитываем как для диска; следовательно, J ₁= ¹1₂m ₁ R². Момент инерции человека рассчитываем как для материальной точки. Поэтому J ₂=0, J' ₂ =m ₂ R ². Угловая скорость платформы до перехода человека равна .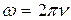

Заменив в формуле (3) величины J ₁, J ₂, J' ₂. и их выражениями, получим:

Сделав подстановку значений т ₁, т ₂, , R и , найдем линейную скорость человека:

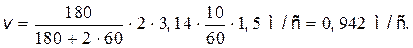
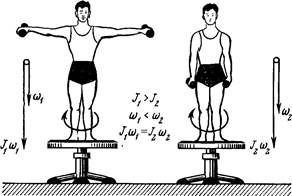Пример 18. Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции. Частота вращения ₁=0,5 c^-1. Момент инерции j_o тела человека относительно оси вращения равен 1,6 кг·м². В вытянутых в стороны руках человек держит по гире массой m =2 кг каждая. Расстояние между гирями l ₁=l,6 м. Опре­делить частоту вращения ₂, скамьи с человеком, когда он опустит руки и расстояние l ₂ между гирями станет равным 0,4 м. Моментом инерции скамьи пренебречь.

Решение. Человек, держащий гири (рис. 12), составляет вместе со скамьей замкнутую механическую систему, поэтому момент импульса J этой системы должен иметь постоянное значение. Следовательно, для данного случая

J₁ = J₂ ,

где J и — момент инерции тела человека и угловая скорость скамьи и человека с вытянутыми руками; J ₂ и — момент инерции тела человека и угловая скорость скамьи и человека с опу­щенными руками. Отсюда:

= (J ₁/ J ₂) .

Выразив в этом уравнении угловые скорости и через частоты вращения ₁ и ₂ ( =2 ) и сократив на 2 , получим:

₂=(J₁/J₂) ₁. (1)

Момент инерции системы, рассматриваемой в данной задаче, равен сумме момента инерции тела человека J₀ и момента инерции гирь в руках человека. Так как размер гирь много меньше расстояния их от оси вращения, то момент инерции гирь можно определить по формуле момента инерции материальной точки: J=mr². Следовательно,

J ₁= J ₀+2 m (l ₁/2)²;

где т — масса каждой из гирь; l ₁ и l ₂. — первоначальное и конечное расстояние между гирями. Подставив выражения J ₁ и J ₂ в уравнение (1), получим:

. (2)

Выполнив вычисления по формуле (2), найдем

₂=1,18 с^-1.

Пример 19. Стержень длиной l =1,5 м и массой М= 10 кг может вращаться вокруг неподвижной оси, проходящей через верх­ний конец стержня (рис. 13). В середину стержня ударяет пуля массой m =10 г, летящая в горизонтальном направлении со скоростью v_o =500 м/с, и застревает в стержне. На какой угол отклонится стержень после удара?

Решение. Удар пули следует рассматривать как неупругий: после удара и пуля, и соответствующая точка стержня будут двигаться с одинаковыми скоростями.

Рассмотрим подробнее явления, происходящие при ударе. Сначала пуля, ударившись о стержень, за ничтожно малый промежуток времени приводит его в движение с угловой скоростью и сообщает ему кинетическую энергию

(1)

где — момент инерции стержня относительно оси вращения.

Затем стержень поворачивается на искомый угол , причем центр масс его поднимается на высоту . В отклоненном положении стержень бу

Date: 2015-12-10; view: 500; Нарушение авторских прав