
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Векторы и линейные операции над векторами. Разложение векторов
|
|
Тема 3. Векторная алгебра
Векторы и линейные операции над векторами. Разложение векторов
Определение 3.1 Вектором (геометрическим вектором) называется направленный отрезок, то есть отрезок, имеющий определенную длину и направление.
Векторы рассматриваются на плоскости (двумерные) и в пространстве (трехмерные). И в том, и в другом случае вектор определяется упорядоченной парой точек, первая из которых – начало вектора, другая – конец вектора. Для обозначения векторов используются символы  ,
, 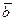 ,
,  ,
, 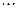 . Если
. Если  и
и  соответственно точки начала и конца вектора, то этот вектор обозначается
соответственно точки начала и конца вектора, то этот вектор обозначается  (Рис. 3.1). Вектор
(Рис. 3.1). Вектор  с началом в точке
с началом в точке  и концом в точке
и концом в точке  называет противоположным вектору
называет противоположным вектору  .
.

Длиной или модулем  вектора
вектора  называется число, равное длине отрезка
называется число, равное длине отрезка  , изображающего вектор. Векторы
, изображающего вектор. Векторы  и
и  имеют один и тот же модуль.
имеют один и тот же модуль.
Нулевым вектором называется вектор, начало и конец которого совпадают. Нуль-вектор обозначается символом  . Модуль нулевого вектора равен нулю.
. Модуль нулевого вектора равен нулю.
Единичным вектором называет вектор, длина которого равна единице. Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  и обозначается
и обозначается  .
.
Два ненулевых вектора называются равными, если один из них путем параллельного переноса можно совместить с другим так, что совпадут их начала и концы (рис 1.2). Обозначают  .
.

С точки зрения векторной алгебры вектор не меняется при его параллельном переносе с сохранением его длины и его направления, то есть точку приложения вектора можно помещать в любую точку пространства. Такие векторы называются свободными.
Линейными операциями над векторами называются операции сложение, вычитание и умножение вектора на число.
Сложение двух векторов  и
и 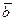 можно выполнить с помощью правила параллелограмма. Если отложить векторы
можно выполнить с помощью правила параллелограмма. Если отложить векторы  и
и 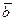 от общей точки
от общей точки 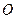 и построить на них как на сторонах параллелограмм, то вектор
и построить на них как на сторонах параллелограмм, то вектор  , идущий из общего начала
, идущий из общего начала 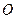 в противоположную вершину параллелограмма, будет их суммой
в противоположную вершину параллелограмма, будет их суммой  (рис. 3.3).
(рис. 3.3).

Для построения суммарного вектора  не обязательно строить весь параллелограмм
не обязательно строить весь параллелограмм  , достаточно построить треугольник
, достаточно построить треугольник  . Сформулированное правило определения суммы можно заменить более удобным.
. Сформулированное правило определения суммы можно заменить более удобным.
Суммой двух векторов  и
и 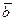 называется вектор, соединяющий начало первого слагаемого вектора
называется вектор, соединяющий начало первого слагаемого вектора  с концом второго при условии, что начало второго слагаемого совмещено с концом первого (рис. 3.4).
с концом второго при условии, что начало второго слагаемого совмещено с концом первого (рис. 3.4).

При этом ясно, что результат сложения не зависит от того, в какой точке пространства начало первого слагаемого: при её изменении весь треугольник параллельно переносится. Это правило сложения векторов называется правилом треугольника.
Сложение многих векторов  ,
, 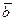 ,
,  ,
,  ,
, 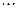 совершается последовательно: сначала складывается первый вектор
совершается последовательно: сначала складывается первый вектор  со вторым
со вторым 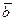 , затем к их сумме прибавляется третий вектор
, затем к их сумме прибавляется третий вектор  , затем к полученной сумме
, затем к полученной сумме  прибавляется вектор
прибавляется вектор  и т.д. (рис. 3.5).
и т.д. (рис. 3.5).
Непосредственно видно, что получается следующее правило для сложения векторов.
Правило многоугольника. Суммой нескольких векторов является вектор, соединяющий начало первого слагаемого вектора с концом последнего при условии, что начало каждого последующего вектора совмещено с концом предыдущего (рис. 3.6).


Законы сложения векторов:
1.  ,
,
2.  ,
,
3.  .
.
Разностью двух векторов  и
и 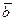 называется вектор
называется вектор  , который при сложении с вектором
, который при сложении с вектором 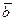 даёт вектор
даёт вектор  (рис. 3.7).
(рис. 3.7).

Заметим, что если на векторах  и
и 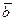 , отложенных от общего начала, можно построить параллелограмм, то одна направленная диагональ является суммой векторов, а другая разностью.
, отложенных от общего начала, можно построить параллелограмм, то одна направленная диагональ является суммой векторов, а другая разностью.
Произведением ненулевого вектора  на число
на число  называется вектор
называется вектор  (или
(или  ), длина которого равна
), длина которого равна  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  , при
, при  и противоположно ему при
и противоположно ему при  .
.
 Например, если дан вектор
Например, если дан вектор  , то векторы
, то векторы  и
и  имеют вид
имеют вид  и
и 
 .
.
Законы умножения вектора на число:
1.  ,
,
2.  ,
,
3.  ,
,
4.  .
.
Из определения произведения вектора на число следует, что всякий вектор  может быть представлен в виде произведения модуля вектора на орт этого вектора.
может быть представлен в виде произведения модуля вектора на орт этого вектора.
 (3.1)
(3.1)
Если над векторами  ,
, 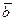 ,
,  ,
,  выполнять действия сложения, вычитания и умножения на число, то в результате любого числа таких действий получится вектор вида
выполнять действия сложения, вычитания и умножения на число, то в результате любого числа таких действий получится вектор вида
 ,
,
представляющий собой линейную комбинацию исходных векторов.
Векторы  ,
, 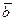 ,
,  ,
,  называются линейно зависимыми (связанными линейной зависимостью), если между ними выполняется соотношение следующего вида:
называются линейно зависимыми (связанными линейной зависимостью), если между ними выполняется соотношение следующего вида:
 , (3.2)
, (3.2)
где скалярные коэффициенты  не все равны нулю.
не все равны нулю.
Если все коэффициенты равны нулю, то соотношение (3.2) будет выполняться, но оно не будет устанавливать зависимости между векторами. Про векторы  ,
, 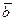 ,
,  ,
,  говорят, что они линейно независимые.
говорят, что они линейно независимые.
Понятие линейной независимости между векторами используется для алгебраической характеристики взаимного расположения векторов в пространстве.
Определение 3.2 Два ненулевых вектора  и
и 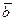 называются коллинеарными (обозначают
называются коллинеарными (обозначают  ), если они лежат на одной прямой или на параллельных прямых.
), если они лежат на одной прямой или на параллельных прямых.
Коллинеарные векторы могут быть одинаково направленными (как векторы  и
и  ) или противоположно направленными (векторы
) или противоположно направленными (векторы 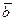 и
и  (рис 3.8)).
(рис 3.8)).

Теорема 3.1 Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Следствие. Если между двумя неколлинеарными векторами выполняется равенство
 ,
,
то оба коэффициента должны равняться нулю  .
.
Определение 3.3 Ненулевые векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Любые два вектора всегда компланарны, а три вектора могут и не быть компланарными.
Теорема 3.2 Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
 - коллинеарны
- коллинеарны  (3.3)
(3.3)
Представление вектора  в виде линейной комбинации векторов
в виде линейной комбинации векторов  и
и 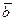 по (3.3) называется разложением
по (3.3) называется разложением  на плоскости по двум неколлинеарным векторам.
на плоскости по двум неколлинеарным векторам.
Рассмотрим произвольный вектор  и тройку некомпланарных векторов
и тройку некомпланарных векторов  .
.
Теорема 3.3 Каждый вектор  единственным образом разлагается по трем некомпланарным векторам
единственным образом разлагается по трем некомпланарным векторам  , т.е. представляется в виде
, т.е. представляется в виде
 (3.4)
(3.4)
Из (3.4) следует, что любые четыре вектора в пространстве линейно зависимы.
Упорядоченная тройка некомпланарных (линейно независимых) векторов  называется базисом во множестве геометрических векторов пространства. Скалярные коэффициенты
называется базисом во множестве геометрических векторов пространства. Скалярные коэффициенты  однозначно определяются и называются координатами вектора
однозначно определяются и называются координатами вектора  относительно базиса
относительно базиса  .
.
Аналогично: упорядоченная пара  неколлинеарных (линейно независимых) векторов образует базис геометрических векторов на плоскости. Коэффициенты
неколлинеарных (линейно независимых) векторов образует базис геометрических векторов на плоскости. Коэффициенты  в разложении (3.4) есть координаты вектора
в разложении (3.4) есть координаты вектора  относительно базиса
относительно базиса  .
.
Date: 2015-12-10; view: 478; Нарушение авторских прав