
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прямая на плоскости
|
|
Линия на плоскости рассматривается (задается) как множество точек, обладающих некоторым, только им присущим геометрическим свойством.
Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел - ее координат, а положение линии на плоскости определять с помощью уравнения (то есть равенства, связывающего координаты точек линии).
Определение. Уравнением линии (или кривой) на плоскости Oxy называется такое уравнение  с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют коорлинаты любой точки, не лежащей на этой линии.
с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют коорлинаты любой точки, не лежащей на этой линии.
Переменные x и у в уравнении линии называются текущими координатами точек линии.
Пример 24. Лежат ли точки  и
и  на линии
на линии 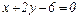 ?
?
Решение. Подставив в уравнение линии вместо x и у координаты точки А, получим  . Значит точка А не лежит на данной линии.
. Значит точка А не лежит на данной линии.
Подставим в уравнение линии координаты точки В вместо x и у  . Следовательно, точка В лежит на данной линии.
. Следовательно, точка В лежит на данной линии.
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разнее виды уравнений прямой.
Пусть 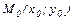 - заданная точка прямой l. Вектор
- заданная точка прямой l. Вектор  , перпендикулярный прямой l, называют нормальным вектором прямой. Пусть
, перпендикулярный прямой l, называют нормальным вектором прямой. Пусть  - произвольная (текущая) точка прямой. l. Тогда
- произвольная (текущая) точка прямой. l. Тогда 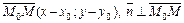 . По свойствам скалярного произведения
. По свойствам скалярного произведения 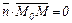 , то есть
, то есть
 (2.25)
(2.25)
Полученное уравнение называется уравнением прямой, проходящей через данную точку перпендикулярно данному вектору.







Раскрыв скобки и сгрупировав слогаемые в (2.25), получим  . Обозначим
. Обозначим  , уравнение (2.25) примет вид
, уравнение (2.25) примет вид
 , (2.26)
, (2.26)
которое называется общим уравнением прямой на плоскости.
Некоторые частные случаи общего уравнения прямой:
1) если  , то уравнение приводится к виду
, то уравнение приводится к виду  . Это есть уравнение прямой, параллельной оси Ох;
. Это есть уравнение прямой, параллельной оси Ох;
2) если  , то уравнение приводится к виду
, то уравнение приводится к виду  , прямая параллельна оси Оу;
, прямая параллельна оси Оу;
3) если 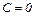 ,
,  , то получим
, то получим  , прямая проходит через начало координат;
, прямая проходит через начало координат;
4)если  , уравнение прямой принимает вид
, уравнение прямой принимает вид  или
или  , прямая проходит через ось Ох;
, прямая проходит через ось Ох;
5)если  , уравнение прямой
, уравнение прямой  , или х=0, прямая проходит через ось Оу.
, или х=0, прямая проходит через ось Оу.
Пусть в уравнении (2.26) 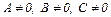 , тогда перенесем слогаемое С в правую часть и разделим на него обе части уравнения
, тогда перенесем слогаемое С в правую часть и разделим на него обе части уравнения
 , или
, или  .
.
Обозначив  ,
,  , получим уравнение
, получим уравнение
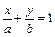 , (2.27)
, (2.27)
которое называется уравнением прямой в отрезках, здесь а и b - отрезки, отсекаемые прямой на осях координат.

Определение. Вектор  , параллельный прямой, называется направляющим вектором прямой.
, параллельный прямой, называется направляющим вектором прямой.

Пусть  - заданная точка на прямой l,
- заданная точка на прямой l,  - направляющий вектор этой прямой,
- направляющий вектор этой прямой,  - произвольная точка прямой l. Тогда
- произвольная точка прямой l. Тогда  ,
,  . Используя условие (2.13), получим:
. Используя условие (2.13), получим:
 (2.28)
(2.28)
Полученное уравнение (2.28) называется каноническим уравнением прямой, или уравнением прямой, проходящей через данную точку параллельно данному вектору.

В частности, если прямая l параллельна оси Ох, то ее направляющий вектор  и уравнение (2.28) имеет вид
и уравнение (2.28) имеет вид  , или
, или 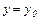 .
.
Если  , то
, то  и уравнение прямой
и уравнение прямой 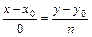 , или
, или 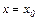 .
.
Если в уравнении (2.28) величину отношения положить равной t (t - параметр, переменная величина,  ):
): 
 , то, выразив х и у из уравнений, получим
, то, выразив х и у из уравнений, получим
 ,
,  . (2.29)
. (2.29)
Уравнения (2.29) называются параметрическими уравнениями прямой.
Пусть на прямой l заданы две точки  и
и  . Тогда вектор
. Тогда вектор 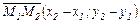 является направляющим вектором прямой и, используя уравнение (2.28), можно записать
является направляющим вектором прямой и, используя уравнение (2.28), можно записать
 (2.30)
(2.30)
Уравнение (2.30) - уравнение прямой, проходящей через две данные точки. Пусть  - заданная точка на прямой l,
- заданная точка на прямой l,  - угол наклона прямой к оси Ох,
- угол наклона прямой к оси Ох,  . В качестве направляющего вектора прямой l возьмем единичный вектор
. В качестве направляющего вектора прямой l возьмем единичный вектор 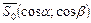 , но
, но  , тогда
, тогда  , то есть
, то есть  . Используя уравнение (2.28), получим
. Используя уравнение (2.28), получим  или
или  . Обозначим
. Обозначим  (k - угловой коэффициент прямой), получим уравнение прямой, проходящей через данную точку в заданном направлении
(k - угловой коэффициент прямой), получим уравнение прямой, проходящей через данную точку в заданном направлении
 . (2.31)
. (2.31)

Выразив из (2.31) у:  и обозначив
и обозначив 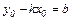 , получим уравнение
, получим уравнение
 (2.32)
(2.32)
которое называется уравнением прямой с угловым коэффициентом. В уравнении (2.32) b - ордината точки пересечения прямой с осью Оу.
Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых.
Пусть прямые  и
и 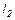 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами 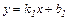 и
и  , где
, где  ,
,  .
.
Требуется найти угол  , на который надо повернуть в положительном направлении прямую
, на который надо повернуть в положительном направлении прямую  вокруг точки их пересечения до совпадения с прямой
вокруг точки их пересечения до совпадения с прямой 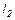 .
.

 (по теореме о внешнем угле треугольника) или
(по теореме о внешнем угле треугольника) или  . Если
. Если  , то
, то  Таким образом
Таким образом
 (2.33)
(2.33)
Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая - второй, то правая часть формулы (2.33) берется по модулю, то есть
 (2.34)
(2.34)
Если  , то
, то  и
и  . Из формулы (2.33) следует, что
. Из формулы (2.33) следует, что  , то есть
, то есть
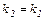 . (2.35)
. (2.35)
Если  , то
, то  . Тогда
. Тогда  .
.
Отсюда 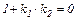 , то есть
, то есть
 (или
(или  ). (2.36)
). (2.36)
Если прямые  и
и 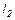 заданы общими уравнениями
заданы общими уравнениями 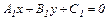 и
и  , где
, где  и
и  - нормальные векторы прямых, то
- нормальные векторы прямых, то
 или
или
 (2.37)
(2.37)
Если  , то
, то 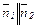 , следовательно
, следовательно
 (2.38)
(2.38)
Если  , то
, то  , то есть
, то есть 
 . (2.39)
. (2.39)
Date: 2015-12-10; view: 387; Нарушение авторских прав