Скалярное произведение векторов и его свойства

Определение. Скалярным произведением двух ненулевых векторов и (, ) называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается ,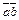

, (2.16)

где .

Формулу (2.16) можно записать иначе. Так как , , то получаем:

(2.17)

то есть скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства скалярного произведения:

1)

2)

3) ;

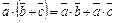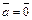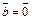4) тогда и только тогда, когда , или , или ;

5) - скалярный квадрат вектора равен квадрату его длины.

Пусть заданы два вектора и .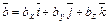

Тогда Таким образом,

(2.18)

Пример 11. Даны векторы . Найти скалярное произведение .

Решение. Воспользуемся свойствами 2, 3:

.

Используя формулу (2.18), получаем:

Тогда

Пример 12. Найти длину вектора , если .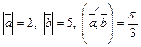

Решение. Используя свойство 5 скалярного произведения, получаем

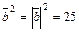, но , , , следовательно, .

Пример 13. Даны векторы , 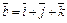. Найти угол между векторами 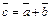и .

Решение. Найдем координаты векторов и :

, то есть ;

, то есть .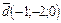

Воспользуемся формулой (2.16) ,

тогда

.

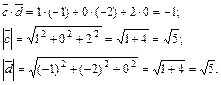
Следовательно

тогда

Пример 14. Даны векторы , , 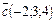. Найти вектор , если известно, что

Решение. Пусть искомый вектор . Из условия следует, что или то есть .

Из условия следует, что или , то есть .

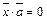Из условия следует, что или .

Из полученных равенств составим систему линейных уравнений, решение которой и определит координаты искомого вектора .

Решим систему уравнений методом Гаусса. Для этого составим расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

.

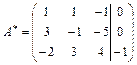Элементы первой строки матрицы умножим на (-3) и прибавим к соответствующим элементам второй строки, затем элементы первой строки умножим на 2 и прибавим к соответствующим элементам третьей строки:

~ .

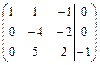Элементы второй строки полученной матрицы умножим на :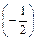

~ .

Элементы второй строки умножим на (-5), третьей строки – на 2, затем к полученным элементам третьей строки прибавим соответственные полученные элементы второй строки:

~ .

С помощью полученной матрицы треугольного вида составим систему уравнений, равносильную системе .

Таким образом, искомый вектор .

Date: 2015-12-10; view: 362; Нарушение авторских прав