Обратная матрица. Пусть А-квадратная матрица n-го порядка

Пусть А -квадратная матрица n- го порядка

.

Определение. Матрица

составленная из алгебраических дополнений к элементам матрицы А, называется присоединенной к матрице А.

Алгебраические дополнения к элементам квадратной матрицы находятся так же, как к элементам ее определителя. В присоединенной матрице алгебраические дополнения элементов строки стоят в столбце с таким же номером.

Пример 23. Дана матрица

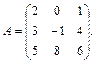
Найти матрицу, присоединенную к матрице А.

Решение. Найдем алгебраические дополнения к элементам матрицы А:

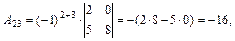
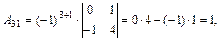
Составим матрицу , присоединенную к матрице А

.

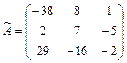Определение. Матрица называется обратной матрице А, если выполняется условие

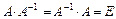, (1.14)

где Е – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А..

Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы 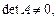то есть чтобы матрица была невырожденной.

Обратная матрица находится по формуле:

(1.15)

для матрицы А третьего порядка.

Свойства обратной матрицы:

1.

2.

3.

Пример 24. Найти , если

Решение. Проверим, является ли данная матрица невырожденной. Вычислим определитель, соответствующий матрице А:

следовательно матрица А невырожденная и для нее существует обратная матрица .

Найдем алгебраические дополнения элементов матрицы А:

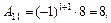
Составим матрицу по формуле (1.15)

Проверка:

Следовательно, обратная матрица найдена верно.

Пример 25. Показать, что матрица А является обратной для В, если

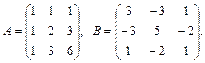
Решение. Найдем произведение матриц А и В:

Следовательно, матрица А является обратной для матрицы В.

Пример 26. Найти матрицу, обратную для матрицы

Решение. Найдем определитель матрицы А:

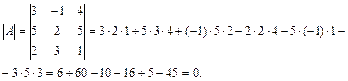
Матрица А – вырожденная, значит обратная для нее матрица не существует.

Пример 27. Найти матрицу, обратную для данной матрицы

Решение. Найдем определитель матрицы А:

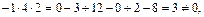
значит матрица А невырожденнаяи для нее существует обратная матрица .

Вычислим алгебраические дополнения элементов матрицы А:

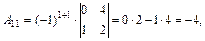
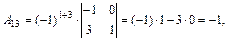
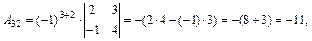
Используя формулу (1.15), составим матрицу :

.

Проверка:

Значит обратная матрица найдена верно.

Date: 2015-12-10; view: 413; Нарушение авторских прав