
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Срез и смятие, основные расчетные предпосылки, условия расчета
|
|
Заклепочные (болтовые) соединения (рис. 36.1) работают на срез и смятие.

Рис. 36.1. Схема заклепочного соединения
Площадь среза одной заклепки определяется по формуле:
 .
.
Если число заклепок в соединении равно n, то
 .
.
Соединение внахлестку имеет недостаток в том, что листы располагаются не в одной плоскости, вследствие чего силы F образуют пару сил, вызывающих изгиб листов и перекашивание соединения. Более рационально соединение листов впритык с накладками (рис. 36.2).
В таком соединении каждая заклепка испытывает напряжения среза по двум плоскостям. Такие заклепки называется двухсрезными заклепками.

Рис. 36.2. Схема соединения листов впритык с помощью накладок
Если число плоскостей среза обозначить через m, то площадь среза соединения определяется по формуле
 ,
,
где n – число заклепок, расположенных по одну сторону стыка.
Условие прочности соединения на срез имеет вид
 .
.
Данное условие позволяет выполнять три вида расчетов на прочность – проверочный, проектировочный и определение максимально допустимой нагрузки на соединение.
Проектировочный расчет обычно заключается в определении диаметра d заклепок, если их количество п задано конструктивно. Таким образом:
 .
.
Если конструктивно назначается диаметр заклепок d, то определяют их общее количество по формуле:
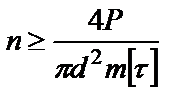 .
.
Количество срезов заклепки m определяется конструкцией соединения.
Деформация сдвига часто сопровождается смятием.
В заклепочных и болтовых соединениях напряжения смятия распределяются неравномерно по полуцилиндрической поверхности отверстия листа и заклепки и имеют наибольшую величину в точке К (рис. 36.3, а).
Для упрощения расчетов условно принимают, что смятие происходит по площади тпрr.
А см = td,
где d – диаметр заклепочного отверстия;
t – толщина листа.
Если заклепка соединяет два листа неодинаковой толщины, то в формулу следует подставить меньшую из них.
Для двухсрезных заклепок условной площадью смятия является:
А см = td, или А см = 2 t 1 d.
В расчете принимают меньшую из этих двух величин.

Рис. 36.3. Схема для расчета заклепки на смятие
Условие прочности соединения на смятие принимает вид:
 ,
,
где n – число заклепок;
[ σ см] – допускаемое напряжение на смятие, для стали оно принимается [ σ см] = (2…2,5) [ σ ].
Расчет болтовых и заклепочных соединений на смятие проводится как проверочный.
Косой изгиб, основные понятия и определения
Косым называют такой вид изгиба, при котором все внешние нагрузки, вызывающие изгиб, действуют в одной силовой плоскости, не совпадающей ни с одной из главных плоскостей.
Рассмотрим брус, защемленный одним концом и загруженный на свободном конце силой F (рис. 37.1).

Рис. 37.1. Расчетная схема к косому изгибу
Внешняя сила F приложена под углом  к оси y. Разложим силу F на составляющие, лежащие в главных плоскостях бруса, тогда:
к оси y. Разложим силу F на составляющие, лежащие в главных плоскостях бруса, тогда:


Изгибающие моменты в произвольном сечении, взятом на расстоянии z от свободного конца, будут равны:


Нормальные напряжения в поперечном сечении бруса при косом изгибе определяются по формуле:

Для нахождения наибольших растягивающих и сжимающих нормальных напряжений при косом изгибе необходимо выбрать опасное сечение бруса.
Если изгибающие моменты | Мх | и | Му | достигают наибольших значений в некотором сечении, то это и есть опасное сечении.
Таким образом, 
Положение нейтральной оси при косом изгибе определяется по формуле:

тогда

где  угол наклона нейтральной оси к оси х;
угол наклона нейтральной оси к оси х;
 угол наклона силовой плоскости к оси у (рис. 11.3).
угол наклона силовой плоскости к оси у (рис. 11.3).
В опасном сечении бруса (в заделке, рис. 37.1) напряжения в угловых точках определяются по формулам:


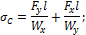

При косом изгибе нейтральная ось делит сечение бруса на две зоны – зону растяжения и зону сжатия. Для прямоугольного сечения эти зоны показаны на рис. 37.2.

Рис. 37.2. Схема сечения защемленного бруса при косом изгибе
Для определения экстремальных растягивающих и сжимающих напряжений необходимо провести касательные к сечению в зонах растяжения и сжатия, параллельные нейтральной оси (рис. 37.2).
Наиболее удаленные от нейтральной оси точки касания А и С – опасные точки в зонах сжатия и растяжения соответственно.
Для пластичных материалов условие прочности можно представить в виде:

Для симметричных сечений (прямоугольник, двутавровое сечение) условие прочности имеет следующий вид:

Из условия прочности вытекает три вида расчетов:
- проверочный;
- проектировочный – определение геометрических размеров сечения;
- определение несущей способности бруса (допускаемой нагрузки).
Внецентренное растяжение-сжатие, основные понятия и определения
Внецентренным растяжением (сжатием) называется такой вид деформации, при котором растягивающая (сжимающая) сила параллельна продольной оси бруса, но точка ее приложения не совпадает с центром тяжести поперечного сечения (рис. 38.1).

Рис. 38.1. Схема бруса при внецентренном сжатии
Если перенести силу F параллельно самой себе из точки С в центр тяжести сечения, то внецентренное сжатие можно представить как сумму трех простых деформаций: сжатия и изгиба в двух плоскостях (рис. 38.1, б). При этом имеем:
 ,
, 
Напряжения в произвольной точке сечения при внецентренном сжатии, лежащей в первом квадранте, с координатами x и y можно найти исходя из принципа независимости действия сил:

Так как


где x и y – координаты точки сечения, в которой определяется напряжение.
Обозначим координаты точек нейтральной оси через x 0 и y0. Так как в точках нейтральной оси  0, то приравняем правую часть уравнения для определения нормальных напряжений к нулю. С учетом того, что
0, то приравняем правую часть уравнения для определения нормальных напряжений к нулю. С учетом того, что


Это уравнение прямой, не проходящей через начало
координат. Определим отрезки ах и ay, отсекаемые нейтральной осью на координатных осях (рис. 38.2).
Приу0 = 0 получим следующее выражение:
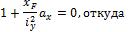

Рис. 38.2. Схема для определения отрезков, отсекаемых
нейтральной осью на осях координат

Аналогично при x 0 = 0, имеем:


Знак «минус» в данных формулах указывает на то, что точка приложения силы C и нейтральная ось всегда расположены по разные стороны от центра тяжести сечения.
Положение нейтральной оси зависит от координат точки приложения нагрузки – чем ближе сила приложена к центру тяжести сечения, тем дальше от него расположена нейтральная ось.
Область вокруг центра тяжести сечения, характерная тем, что всякая продольная сила, расположенная внутри или по границе этой области, вызывает во всех точках поперечного сечения напряжения одного знака, называется ядром сечения.
Координаты границ ядра сечения можно определить по формулам:

Кручение вала круглого поперечного сечения, основные понятия и определения
Кручением называется такой вид деформации, при котором в поперечных сечениях элементов конструкций возникает только крутящий момент Мкр, а другие внутренние силовые факторы (продольная сила, изгибающие моменты, поперечные силы) равны нулю.
 Выделим часть вала длиной dz между двумя поперечными сечениями. Считаем, что правое сечение закреплено в заделке, а левое сечение закручивается моментом Мкр (рис. 39.1, б). При этом точка А остается неподвижной, а точка B переместится в положение
Выделим часть вала длиной dz между двумя поперечными сечениями. Считаем, что правое сечение закреплено в заделке, а левое сечение закручивается моментом Мкр (рис. 39.1, б). При этом точка А остается неподвижной, а точка B переместится в положение  . Мысленно вырежем в выделенном элементе внутреннюю часть с наружным радиусом ρ. Получим кольцевое сечение толщиной dρ. Определим значение
. Мысленно вырежем в выделенном элементе внутреннюю часть с наружным радиусом ρ. Получим кольцевое сечение толщиной dρ. Определим значение  из
из 
Рис. 39.1. Схема выделенной части вала длиной dz
Из  имеем:
имеем:
 ,
,
учитывая, что при малых деформациях 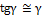 , получим
, получим

С другой стороны, из  :
:

Окончательно получим:
 ,
,
откуда

где  угол сдвига,
угол сдвига,
 абсолютный угол закручивания, [рад].
абсолютный угол закручивания, [рад].
Обозначим


Используя закон Гука при сдвиге, получим:
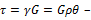 величина касательных напряжений в сечении вала на расстоянии
величина касательных напряжений в сечении вала на расстоянии  от центра тяжести сечения;
от центра тяжести сечения;  модуль сдвига.
модуль сдвига.
На основании полученной формулы можно сделать вывод, что  в сечении вала распределяются по линейному закону и максимальные касательные напряжения
в сечении вала распределяются по линейному закону и максимальные касательные напряжения  возникают на поверхности вала. В центре вала касательные напряжения равны нулю.
возникают на поверхности вала. В центре вала касательные напряжения равны нулю.
Распределение касательных напряжений по сечению вала показано на рис. 39.2.

Рис. 39.2. Схема распределения касательных
напряжений по сечению вала
Величину крутящего момента Mкр можно определить через t. Момент относительно оси z от действия касательных напряжений t на элементарной площадке dА равен (рис. 39.3):
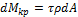 .
.

Рис. 39.3 Схема для определения Мкр
в сечении вала
Проинтегрировав это выражение по площади поперечного сечения вала, получим:

Пусть геометрические размеры поперечного сечения вала одинаковы по длине. Материал вала однороден и изотропен. Подставим в интеграл выражение  , получим:
, получим:


Правило знаков для крутящих моментов.
Если крутящий момент со стороны внешней нормали n к сечению вала вращается против часовой стрелки, то он считается положительным (рис. 39.4), в противном случае – крутящий момент считается отрицательным.

Рис. 10.5. Схема для определения знаков крутящих
моментов в сечениях вала
Из выражения крутящего момента при кручении определим относительный угол закручивания  :
:

где 
Тогда, если длина вала равна 

если  , то решение интеграла принимает вид
, то решение интеграла принимает вид

где  угол закручивания сечения в начале системы отсчета.
угол закручивания сечения в начале системы отсчета.
Условие прочности при кручении:

Из этого неравенства определяется полярный момент сопротивления:

Для вала круглого поперечного сечения имеем:
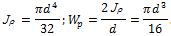
Решая данное уравнение относительно диаметра с учетом условия прочности, получим следующую расчетную формулу:
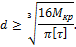
Если выбрать значение d несколько меньше расчетного диаметра, то необходимо выполнить проверочный расчет и убедиться, что перегрузка вала меньше 5 %, т. е. выполнить последовательно следующий расчет:

Date: 2015-12-10; view: 2862; Нарушение авторских прав