
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Построение эпюр продольных сил, напряжений и перемещений при учете собственного веса стержня
|
|
Для стального ступенчатого стержня квадратного поперечного сечения, сжатого силой F с учетом его собственного веса (рис. 35, а), требуется:
1) определить количество расчетных участков;
2) составить аналитические выражения для нормальных сил N, нормальных напряжений s и вычислить их значения для каждого из участков стержня;
3) вычислить перемещение нижнего конца стержня от действия силы F и собственного веса;
4) построить эпюры N, s и S.
Исходные данные: F = 20 кН; l 1 = l 2 = l 3 = 0,7 м; A 1 = 9 ´ 102 cм2; A 2 = 16 ´ 102 cм2; А 3 = 36 ´ 102 см2; g = 78 ´ 10-6 кН/см3, модуль упругости стали Е = 2,0 ´ 104 кН/cм2;
Решение.
1. Определение количества участков. При определении нормальных сил N границами участков принимаются те сечения, в которых приложены внешние сосредоточенные силы или происходит изменение площади поперечного сечения либо объемного веса материала ступенчатого стержня.
Учитывая, что g = const, стержень будет иметь три участка:
1-й участок - от 0 до сечения b–b (где приложена сила F);
2-й участок - от сечения b–b до сечения c–c;
3-й участок - от сечения c–c до сечения d–d.
При определении нормальных напряжений используем те же участки.
2. Аналитические выражения для нормальных сил N, нормальных напряжений s. Определение их значений для каждого из участков. Воспользуемся методом сечений.
1-й участок (0 - b–b) 0 £ z 1 £ 0,7 м.
Проведем сечение 1-1 на расстоянии z 1 от начала координат (точка 0). Рассмотрим равновесие нижней отсеченной части (рис. 35, б).
Составим уравнение равновесия:

Собственный вес (кН) нижней отсеченной части стержня определяется по формуле:
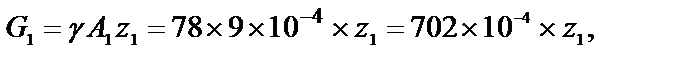
Тогда выражение для нормальной силы (кН) будет иметь вид
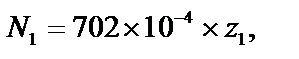
а для нормальных напряжений (кН/см2):
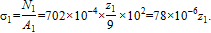
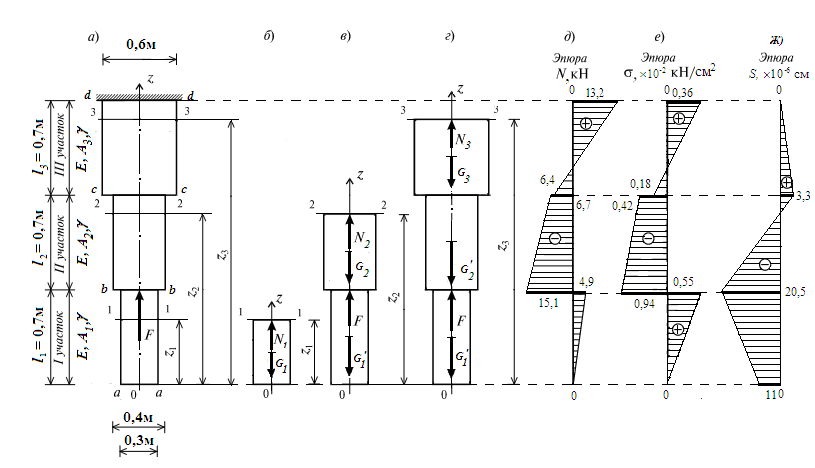
Рис. 35. а – расчетная схема ступенчатого стержня; б – схема отсеченной части, сечение 1–1; в – схема отсеченной части, сечение 2–2; г – схема отсеченной части, сечение 3–3;
д – эпюра нормальных сил; е – эпюра нормальных напряжений; ж – эпюра перемещений характерных сечений
Так как между  (
( ) и z 1 существует линейная зависимость, то для построения эпюр нормальных сил и напряжений достаточно определить значения этих величин на границах 1-го участка, а именно:
) и z 1 существует линейная зависимость, то для построения эпюр нормальных сил и напряжений достаточно определить значения этих величин на границах 1-го участка, а именно:
при z 1 = 0 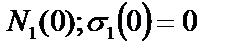 ;
;
при z 1 = 0,7 м 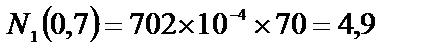 кН;
кН;
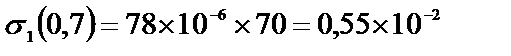 кН/см2.
кН/см2.
2-й участок (b–b - c–c) 0,7 м £ z 2 £ 1,4 м.
Проведем сечение 2-2 на расстоянии z 2 от начала координат (рис. 35, в). Для нижней отсеченной части составляем уравнение равновесия å z = 0, в которое войдут: собственный вес 1-го участка G 1’ = g A 1 l 1; собственный вес отсеченной части 2-го участка G 2 = g A 2 (z 2 – – l 1); сосредоточенная сила F = 20 кН; сила N 2.
Тогда уравнение равновесия примет вид
–G 1’ – G 2 + F + N 2 = 0,
откуда
N 2 = G 1’+ G 2 – F = g´ A 1´ l 1 + g´ A 2´(z 2 – l 1) – F = 78 ´ 9 ´ 10–4 ´ 70 + 78 ´ 16 ´
×10–4 ´ (z 2 – 70) – 20 = 4,9 + 0,12 (z 2 – 70) – 20 = 0,12 (z 2 – 70) – 15,1, кН.
Так как А 2 = const, то выражение для определения нормального напряжения на 2-м участке имеет вид
 кН/см2.
кН/см2.
Вычислим значения ординат N 2 и s2 на границах 2-го участка:
при z 2 = 0,7 м 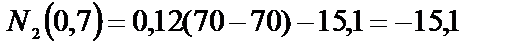 кН;
кН;
 кН/см2;
кН/см2;
при z 2 = 1,4 м 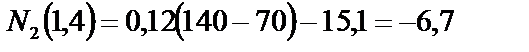 кН;
кН;
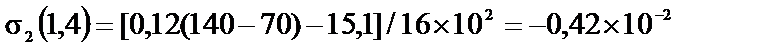 кН/см2.
кН/см2.
3-й участок (c–c - d–d) 1,4 м £ z 3 £ 2,1 м.
Составим уравнение равновесия å z = 0 (рис. 35, г) для нижней отсеченной части стержня:
–G 1’ – G 2’ – G 3 + F + N 3 = 0,
откуда
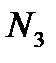 = g A 1 l 1 + g A 2 l 2 + g A 3(z 3 - l 1 - l 2) – F = 78 ´ 9 ´ 10-4 ´ 70 + 78 ´
= g A 1 l 1 + g A 2 l 2 + g A 3(z 3 - l 1 - l 2) – F = 78 ´ 9 ´ 10-4 ´ 70 + 78 ´
×16 ´ 10-4 ´ 70 + 78 ´ 36 ´ 10–4 ´ (z 3 - 140) - 20 = 0,28 ´ (z 3 - 140) – 6,4, кН.
Выражение для напряжения:
 кН/cм2.
кН/cм2.
Вычислим значения ординат N3 и s3 в граничных сечениях 3-го участка:
при z 3 = 1,4 м N 3(1,4) = 0,28 ´ (140 – 140) – 6,4 = –6,4 кН;
s 3 (1,4) = [7,7 ´ (140 – 140) – 177,8] ´10–5 = -0,18 ´ 10–2, кН/cм2;
при z 3 = 2,1 м N 3 (2,1) = 0,28 ´ (210 – 140) – 6,4 = 13,2 кН;
s 3 (2,1) = [7,7 ´ (210 – 140) – 177,8] ´ 10-5 = 0,36 ´ 10–2 кН/cм2.
3. Вычисление перемещения нижнего сечения стержня а–а от действия силы F и собственного веса. Согласно закону Гука определим абсолютные деформации каждого участка стержня по формуле

где 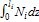 – площадь эпюры
– площадь эпюры 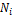 на i- ом участке стержня.
на i- ом участке стержня.
Таким образом,

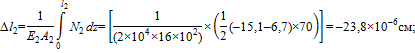

Определим перемещения характерных сечений стержня:
Sd–d = 0 – заделка;
Sc–c = Sd–d + ∆ l 3 = 0 + 3,3 ´ 10–6 = 3,3 ´ 10–6 см;
Sb–b = Sc–c + ∆ l 2 = (3,3 – 23,8) ´ 10–6 см = –20,5 ´ 10–6 см;
Sа–а = Sb–b + ∆ l 1 = (– 20,5 + 9,5) ´ 10–6 см = –11 ´ 10–6 см.
4 .Построение эпюр N, s, S. Так как между N,s, S и координатами z существует линейная зависимость, то для построения эпюр нормальных сил, нормальных напряжений и перемещений достаточно определить значения этих величин в граничных сечениях каждого из участков ступенчатого стержня (рис. 35, д, е, ж).
Необходимыми условиями правильности построения эпюр N,s, S являются:
- скачок на эпюре N должен находиться в точке приложения сосредоточенной силы и быть равным по величине значению этой силы;
- скачки на эпюре s должны совпадать с точками приложения внешней нагрузки F и изменения площади поперечного сечения стержня.
Анализ эпюр N,s, S (рис. 35, д, е, ж) показывает, что они построены правильно.
Date: 2015-12-10; view: 4069; Нарушение авторских прав