Скорость вытеснения одной жидкости другой

В общем случае — непрямолинейного и нерадиального течений — линии тока на границе раздела двух жидкостей испытывают преломление. Построим систему трубок тока в областях, занятых движущимися жидкостями. На границе раздела каждая трубка тока будет иметь излом, перемещающийся вместе с этой границей по мере вытеснения одной жидкости другой. Таким образом, весь процесс течения можно рассматривать как вытеснение одной жидкости другой из системы деформируемых трубок тока, сечения которых изменяются в зависимости от времени.

Вытеснение из недеформируемых трубок тока переменного сечения Предположим, что за все время движения остается неизменной картина линий тока, существовавшая в начальный момент t = 0. Тогда задача сводится к расчету времени вытеснения одной жидкости другой из системы трубок переменного по длине сечения, когда все эти трубки являются уже жесткими, недеформируемыми.

Рассмотрим какую-либо трубку тока переменного сечения (рис. 1.2). Пусть площадь ее поперечного сечения есть функция длины s, отсчитываемой вдоль оси. Будем считать, что скорости фильтрации во всех точках сечения f= f(s) одинаковы.

Рис. 1.2. Трубка тока переменного сечения

Массовыми силами для простоты будем пренебрегать. Кроме того, учет гравитационного эффекта, т. е. различия плотностей, не вносит никаких принципиальных затруднений, и дает небольшую поправку. Из закона Дарси для расхода q, считая жидкости несжимаемыми, имеем

(1.6)

Предположим, что известны давления р₁ и р₂ в сечениях s = s₁ и s = s₂. Выразим q через p₁ и р₂. Для этого из (1.6) найдем

откуда, интегрируя и замечая, что q не зависит от s, получаем

(1.7)

Если проницаемость k переменна, то вместо (1.7) будем иметь

(1.8)

Формулы (1.7) и (1.8) выражают закон Дарси для трубки переменного сечения с равномерным распределением скоростей в поперечных сечениях.

Рассмотрим теперь жесткую трубку переменного сечения длиной l, в которой одна жидкость вытесняет другую. Обозначим вытесняющую жидкость индексом 1, а вытесняемую — индексом 2. Этими же индексами будем обозначать в дальнейшем величины, связанные с вытесняющей или вытесняемой жидкостью. Пусть в одном сечении трубки, занятом вытесняющей жидкостью, давление равно р_к (контур питания), а в другом, отстоящем от первого на расстоянии s =l, занятом вытесняемой жидкостью, равно р_с (скважина).

Предположим, что закон изменения площади f поперечного сечения трубки по длине известен:

(1.9)

Рис. 1.3. Схема контакта двух жидкостей в трубке тока

Пусть первая жидкость занимает в данный момент длину трубки s, а вторая l-s (рис. 1.3). Найдем в этом положении скорость перемещения границы раздела. Обозначая давление в граничном сечении через p_1-2 и считая проницаемость k постоянной, согласно (1.7) получим

. (1.10)

Рассмотрим теперь течение, которое будет в той же трубке, когда она вся будет заполнена только одной жидкостью, например второй вытесняемой, при тех же контурных давлениях р_к и р_с. Давление в этом же сечении s обозначим через р_2-2, скорость u_2-2. Тогда

. (1.11)

Подинтегральные функции в (110) и (1.11) одинаковы, так как трубка тока недеформируема. Тогда, разделив (1.10) на (1.11), найдем

или

(1.12)

где

. (1.13)

Формула (1.13) является искомой. Она позволяет связать скорость u_1-2 двухжидкостной системы со скоростью u_2-2 одножидкостной.

Рис. 1.4. Схема линии тока при прорыве к скважине при различном соотношении вязкостей вытесняемой и вытесняющей жидкостей.

Таким образом, если одножидкостный поток известен, по формуле (1.12) можно найти скорости в любой точке. Отметим, что этот вывод применим и к пространственным потокам.

Очевидно, формула (1.12) будет строго верна для прямолинейного и радиального течений, когда деформаций трубок тока вследствие преломления на границе не происходит. Если траектории частиц в моножидкостной и двухжидкостной системах различны (вязкости жидкостей отличаются), то данная формула дает заниженные или завышенные результаты. В случае существования траекторий общих для обеих жидкостей из геометрических соображений можно судить, в какую сторону делается ошибка при пользовании формулой (1.12).

Пусть вытесняемая жидкость под напором вытесняющей поступает к линейной батарее скважин (рис. 1.4); Т — контур питания, MN — граница раздела в данный момент, AS — прямолинейная осевая линия тока, проходящая через какую-либо скважину S. Рассмотрим примерный вид линии тока в обеих областях, проведенной через точку А', весьма близкую к А. Давления на контурах питания и скважин будем считать неизменными во всех рассматриваемых ниже случаях.

Предположим, что вязкости обеих жидкостей равны, т. е. система одножидкостная. Тогда на границе раздела не будет преломления линий тока и линия тока, проходящая через А', будет изображаться плавной кривой A'B'S. Пусть теперь μ₁≠ μ ₂; тогда линия тока, проходящая через А', будет иметь излом на границе раздела. Если μ₁< μ ₂, то из закона преломления следует, что линия тока будет иметь вид ломаной A'CS, т. е. приблизится к прямой AS. Формула (1.12) соответствует условию неизменности линии A'B'S, чего в действительности не происходит. Таким образом, во второй зоне при μ₁< μ ₂ в окрестности прямой AS происходит сгущение линий тока по сравнению с картиной линий тока при μ₁=μ ₂. Заставляя теперь точку А' стремиться к А, приходим к выводу, что скорость точки В границы раздела, лежащем на прямолинейной траектории AS, в действительности будет несколько больше той величины, которая получится по формуле (1.12), так как сгущение линий тока соответствует увеличению скоростей. Следовательно, эта формула для движения по прямой AS дает при μ₁< μ ₂ несколько заниженное значение скорости против действительной.

Рассуждая совершенно аналогичным образом, мы придем к заключению, что при μ₁> μ ₂ линия тока будет иметь вид A'DS и в этом случае для точки В по формуле (1.12) получится значение скорости, большее действительного. Таким же образом можно показать, что для точки К формула (1.12) будет давать обратные результаты, нежели для точки В, т. е. преувеличенные значения скорости при μ₁< μ ₂ и преуменьшенные при μ₁> μ ₂.

Из этих соображений оказывается возможным установить, в какую сторону мы ошибаемся, пользуясь формулой (1.12).

Вытеснение нефти водой из трубки тока переменного сечения. С задачей о вытеснении нефти водой приходится встречаться при проектировании разработки нефтяных месторождений, когда нужно учесть стягивание контура нефтеносности, а также при расчетах деформации водо-нефтяного контакта. Аналогичные вопросы возникают и при эксплуатации газовых месторождений с краевой или подошвенной водой.

Чтобы охватить по возможности все многообразие частных случаев, рассмотрим следующую задачу. Трубка переменного сечения заполнена пористой средой, в которой одна жидкость вытесняет другую, например вода вытесняет нефть (рис. 1.3). Пусть в одном сечении трубки, рассматриваемом как контур питания в водяной части, известно давление р_к; в другом сечении трубки — в нефтяной части, рассматриваемом как скважины, известно давление р_с. Требуется рассчитать продвижение границы раздела, предполагая, что эта граница является некоторой поверхностью.

В действительности граница раздела вследствие капиллярности и других причин будет размыта, но мы будем предполагать, что она четко очерчена и вытеснение одной жидкости другой происходит «поршневым» образом.

Заметим, что если во втором сечении (в скважинах) будет задан отбор жидкости, то движение границы раздела определяется из простых геометрических соображений, так как объем, образованный движением границы раздела, будет равен объему отобранной жидкости.

Рис.1.5. Схема движения в трубке тока переменного сечения

Прежде чем рассматривать двухжидкостную систему, решим задачу о движении однородной жидкости в трубке переменного сечения f=f(s).

Рассмотрим трубку переменного сечения, где в одном сечении давление p₁ а в другом p₂ (рис. 1.5). Для упрощения задачи будем пренебрегать эффектом силы тяжести. Плотности обеих жидкостей считаются одинаковыми.

Решение задачи получается непосредственно из закона Дарси. Скорость фильтрации u равна

Объемный расход соответственно равен

(1.14)

Знаменатель последней формулы можно назвать фильтрационным сопротивлением и обозначить его через R:

(1.15)

В таком случае формула (1.14) будет записана в виде, аналогичном закону Ома.

(1.16)

Этой формулой воспользуемся для решения задачи движения двух жидкостей, когда одна вытесняет другую.

Очевидно, формулу (1.15) можно применить в отдельности к каждой из областей, занятых водой и нефтью, но для этого надо знать давление р на границе раздела.

Это давление, вообще говоря, переменная величина.

Расход каждой жидкости, воды или нефти, можно следующим образом:

. (1.17)

где μ_в, μ_н — соответственно вязкость воды и нефти; l — вся длина трубки.

Чтобы избавиться от неизвестного промежуточного давления р, сложим числитель и знаменатель по правилу пропорций. Тогда р сократится, и получим

(1.18)

Последняя формула представляет собой не что иное, как закон Ома для последовательного соединения двух проводников (сопротивления складываются).

Рассмотрим более подробно знаменатель этого выражения. Он является переменной величиной, так как зависит от s.

Обозначим

(1.19)

Тогда

(1.20)

Теперь рассмотрим движение границы раздела.

Пусть за время dt граница раздела перейдет длину ds. Тогда из объема f(s)ds уйдет количество нефти, равное объему пор в этом элементе; ушедшее количество нефти заместится равным количеством воды: m f (s)ds = Qdt, откуда, учитывая формулу (1.20), получаем

Для простоты будем считать депрессию постоянной. Разделив переменные, получим

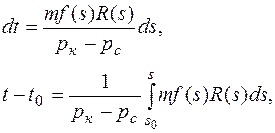(1.21)

где s₀ — положение границы раздела в момент времени t₀. Уравнение (1.20) можно интегрировать также и при других граничных условиях, когда депрессия переменна. В некоторых случаях точное интегрирование оказывается невыполнимым. Тогда применяют методы численного интегрирования.

Рис.1.6. Схема прямолинейного движения водонефтяного контакта

Рассмотрим частные случаи, когда пористость и проницаемость постоянны. Эти частные случаи будут соответствовать тому или другому виду зависимости R(s).

Прямолинейное движение границы раздела в пласте с постоянными мощностью, пористостью и проницаемостью. На рис. 1.6 показан план месторождения; прямая КП — контур питания, на котором поддерживается давление р_к. В нефтяной части расположена прямолинейная батарея скважин. Перед батареей скважин изобары почти прямолинейны. Давление на одной из близких изобар обозначим через р_с. Рассмотрим движение между контуром питания и изобарой р_с.

Решение получится из формул (1.19) и (1.21), где полагаем f (s) = f = const, k = const. Тогда

. (1.22)

Для нахождения закона движения подставим найденное выражение R(s) в формулу (1.21). Тогда получим (полагая t₀ = 0)

(1.23)

Таким образом, задаваясь положением границы раздела, из (1.23) можно найти соответствующее время.

В частности, чтобы найти время полного вытеснения нефти, нужно положить s=l.

Для контроля рассмотрим рассмотрим случай одножидкостной системы. Для одножидкостной системы μ_н=μ_в=μ.

Из (1.23) получим

. (1.24)

Ту же задачу для одножидкостной системы можно решить более просто. Скорость фильтрации u будет постоянна и равна по закону Дарси

.

Скорость самих жидких частиц — действительная скорость движения — получится, если скорость фильтрации разделить на пористость:

.

Так как w= const, то путь s- s₀ будет пройден за время t:

,

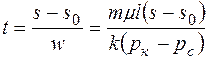что совпадает с (1.24).

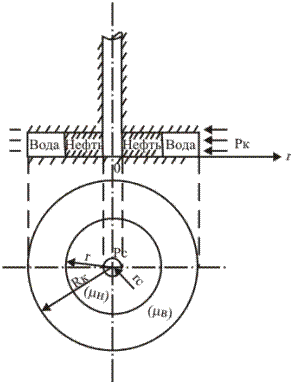Рис.1.7. Схема плоско-радиального движения водонефтяного контакта (s— расстояние, пройденное вытесняющей жидкостью, отсчитываемое от контура питания.

Плоско-радиальное движение водонефтяного контакта в пласте постоянной мощности (рис. 1.7). Пусть жидкость притекает к действительной или воображаемой скважине радиусом г_с, на забое которой поддерживается давление р_с (рис. 1.7, а). В данном случае под «скважиной» подразумевается любая изобара круговой формы.

Контур питания будем считать окружностью радиусом R_K с контурным давлением р_к.

Для этой задачи можно воспользоваться формулой (1.21).

Найдем зависимости f(s) и R(s), учитывая, что f(s) будет величиной переменной и равной f(s)=2πrh, где h —мощность пласта.

Перейдем от переменной s к переменной г (г — радиус перемещающегося контура нефтеносности в данный момент).

Из рис. 1.7, б видно, что s = R_K -г. В таком случае R (s) — фильтрационное сопротивление — согласно формуле (1.19) можно представить в виде:

(1.25)

Это значение фильтрационного сопротивления подставим в общую формулу (1.21) для времени t. Полагая t = 0, получаем

(1.26)

где r₁ и r₂ — радиусы начального и конечного положений водо-нефтяного контакта.

Из формулы (1.26) получаем

(1.27)

Из этой формулы можно найти время радиального перемещения водо-нефтяного контакта от начального положения r=r₁ до заданного г = г₂. Время прорыва в скважину получим, полагая г = г_с.