Пример 1.5

Дебит газовой скважины, приведенный к атмосферному давлению при стандартных условиях Q_aт.ст = 2 млн. м³/сут, абсолютное давление на забое р_с = 12 МПа, толщина пласта h = 10 м, коэффициент пористости пласта m = 12%, коэффициент проницаемости k = 0,5 мкм², плотность газа при стандартных условиях r_ст = 0,750 кг/м³, динамический коэффициент вязкости в пластовых условиях m = 0,015 мПа×с, температура пласта 45°С.

Определить, нарушается ли закону Дарси в призабойной зоне совершенной скважины радиусом г_с = 0,10 м.

Решение:

Определим массовый дебит газа:

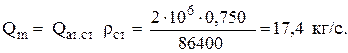
Площадь поперечного сечения на забое скважины

Число Рейнольдса

Ответ: в призабойной зоне закон Дарси нарушается.

Задача 1.1

По керну диаметром 2 см и длиной 5 см за десять минут прокачано 0,6 см³ воды. Абсолютное давление на входе 0,5 МПа, а на выходе 0,2 МПа. Определить действительную скорость и скорость фильтрации на входе в керн, если пористость керна 10%.

Задача 1.2

По керну диаметром 2 см и длиной 5 см за десять минут прокачано 600 см³ газа при стандартных условиях. Абсолютное давление на входе 0,5 МПа, а на выходе 0,1 МПа. Определить действительную скорость и скорость фильтрации на входе в керн, если пористость керна 10%.

Задача 1.3

По керну диаметром 2 см и длиной 5 см за десять минут прокачано 600 см³ газа при стандартных условиях. Абсолютное давление на входе 0,5 МПа, а на выходе 0,1 МПа. Определить действительную скорость и скорость фильтрации на выходе из керна, если пористость керна 10%.

Задача 1.4

Нефтяная галерея в пласте толщиной 10 м за месяц дает 8000 тонн нефти плотностью 780 кг/м³. Ширина галерея 100 м, длина 300 м, пористость пласта 15%. Определить действительную скорость и скорость фильтрации на галерее.

Задача 1.5

Газовая галерея в пласте толщиной 12 м за месяц дает 9000 тонн газа плотностью, при атмосферном давлении, 0,75 кг/м³. Ширина галерея 100 м, длина 300 м, пористость пласта 15%, давление на галерее p_г = 4 МПа. Определить действительную скорость и скорость фильтрации на галерее.

Задача 1.6

Газовая галерея в пласте толщиной 15 м за сутки дает 800 тыс. м³ газа плотностью, при атмосферном давлении, 0,75 кг/м³. Ширина галерея 100 м, длина 300 м, пористость пласта 15%, давление на контуре питания pк = 8 МПа. Определить действительную скорость и скорость фильтрации на контуре питания.

Задача 1.7

Нефтяная совершенная скважина радиусом 0,1 м в пласте толщиной 10 м за один час дает 2 м³ нефти. Определить скорость фильтрации и действительную скорость на скважине, если пористость пласта 15%,.

Задача 1.8

Нефтяная скважина радиусом 0,1 м в пласте толщиной 8 м за 1 час дает 3 м³ нефти и вскрывает пласт на 3 метра. Определить скорость фильтрации и действительную скорость на скважине, пористость пласта 20%

Задача 1.9

Определить среднее значение скорости фильтрации на боковой поверхности гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если толщина пласта h = 25 м, плотность перфорации n_п = 10 отв/м с диаметром отверстий d_п = 1 см, дебит жидкости Q = 250 м^З/сут.

Задача 1.10

За десять дней из скважины добыт объем газа (приведенный к атмосферному давлению и пластовой температуре) W_ат = 15 млн. м³, радиус контура питания r_k = 200 м, толщина пласта h = 20 м, абсолютное давление газа на контуре p_k = 15 МПа. Скорость фильтрации и действительную скорость газа на контуре питания.

Задача 1.11

Определить скорость фильтрации и среднюю скорость движения при плоскорадиальной фильтрации газа к скважине в точке на расстоянии r = 150 м от центра скважины, если давление в этой точке равно р = 8 МПа, толщина пласта h = 12 м, пористость его m = 20%, а приведенный к атмосферному давлению и пластовой температуре дебит Q_ат = 2·10⁶ м³/сут, p_ат = 0,1 МПа.

Задача 1.12

Газовая скважина радиусом 0,1 м в пласте толщиной 20 м за сутки дает 80 тонн газа плотностью ρ_ат = 0,8 кг/м³ и вскрывает пласт на 3 метра. Скважина несовершенна по характеру вскрытия и вскрытая часть скважины имеет плотность перфорации n_п = 10 отв/м с диаметром отверстий d_п = 1 см. Определить скорость фильтрации и действительную скорость на скважине, если давление на скважине 10 МПа, пористость пласта 20%.

Задача 1.13

Определить коэффициент пористости, зная, что действительная скорость движения через образец, определяемая при помощи индикатора, равна v = 5·l0^‑3 см/с, коэффициент проницаемости k = 0,2 мкм², вязкость жидкости μ = 4 мПа·с и разность давлений Dр = 2 МПа при длине образца L = 15 см.

Указание: Найти скорость фильтрации и сравнить с действительной скоростью.

Задача 1.14

В нефтяной галерее давление распределяется по закону p(x) = p_k ‑ (p_k ‑ p_г) x/ L. Определить скорость фильтрации на расстоянии x = 50 м от контура питания, если давление на контуре питания p_к = 8 МПа, давление на галерее p_г = 4 МПа, длина галереи 200 м, проницаемости пласта k = 1 мкм², динамический коэффициент вязкости жидкости μ = 2 мПа·с.

Задача 1.15

В газовой галерее давление распределяется по закону p(x)² = p_k ²‑ (p_k² ‑ p_г²) x/ L. Определить скорость фильтрации на расстоянии x = 50 м от контура питания, если давление на контуре питания p_к = 9 МПа, давление на галерее p_г = 3 МПа, длина галереи 200 м, проницаемости пласта k = 0,1 мкм², динамический коэффициент вязкости газа μ = 0,015 мПа·с.

Задача 1.16

Вокруг нефтяной скважины давление меняется по закону p(r) = p_k ‑ (p_k ‑ p_c) ln(R_k/r)/ln(R_k/r_c). Определить скорость фильтрации на расстоянии r = 10 м от скважины, если давление на контуре питания p_к = 18 МПа, давление на скважине p_с = 14 МПа, радиус контура питания 100 м, проницаемости пласта k = 0,3 мкм², динамический коэффициент вязкости нефти μ = 6,28 мПа·с.

Задача 1.17

Вокруг газовой скважины давление меняется по закону p²(r) = p²_c + (p²_k ‑ p²_c) ln(r/r_c)/ln(R_k/r_c). Определить скорость фильтрации на расстоянии r = 10 м от скважины, если давление на контуре питания p_к = 12 МПа, давление на скважине p_с = 6 МПа, радиус контура питания 100 м, проницаемости пласта k = 0,4 мкм², динамический коэффициент вязкости газа μ = 0,02 мПа·с.

Задача 1.18

Модель пласта представляет собой трубу диаметром 200 мм и длиной 2 м заполненную песком. Труба установлена вертикально. На верхнем конце модели поддерживается манометрическое давление 30 кПа, а нижний конец модели открыт. Определить скорость фильтрации и расход воды, если проницаемости модели k = 0,4 мкм², динамический коэффициент вязкости воды μ = 1 мПа·с.

Задача 1.19

Рис. 1.5.

Определить величину и направление скорости фильтрации в точке А ( Рис. 1.5. ), если проницаемость пласта равна 0,12 мкм², а вязкость нефти 15 мПа·с. Нарисовать вектор скоростей.

Указание. Найти скорости фильтрации вдоль осей x и y.

Задача 1.20

Определить величину и направление скорости фильтрации в точке B ( Рис. 1.5. ), если проницаемость пласта равна 0,15 мкм², а вязкость нефти 15 мПа·с. Нарисовать вектор скоростей.

Указание. Найти скорости фильтрации вдоль осей x и y.

Задача 1.21

Определить величину и направление скорости фильтрации в точке C ( Рис. 1.5. ), если проницаемость пласта равна 0,16 мкм², а вязкость нефти 15 мПа·с. Нарисовать вектор скоростей.

Указание. Найти скорости фильтрации вдоль осей x и y.

Задача 1.22

Определит приведенное относительно ВНК (водонефтяного контакта) давление, в трех наблюдательных скважинах. Манометрические давления в скважинах p_м1 = 18,3 МПа, p_м2 = 18,7 МПа, p_м3 = 17,3 МПа. Глубины спуска манометров H₁ = 2180 м, H₂ = 2280 м, H₃ = 2020 м. Водонефтяной контакт находится на глубине 2320 м. Укажите направление скоростей фильтрации между скважинами. Плотность нефти принять равной 750 кг/м³.

Задача 1.23

Вокруг двух скважин приведенное давление меняется по закону p(x,y) = p_k + Dp₁ ln((x-a)² + y²) + Dp₂ ln((x+a)² + y²). Определить скорость фильтрации в точке с координатами x = 20 м, y = 100 м, если Dp₁ = Dp₂ = 2,6 МПа, a = 100 м, проницаемости пласта 0,4 мкм², динамический коэффициент вязкости нефти μ = 22 мПа·с.

Задача 1.24

Вокруг двух скважин приведенное давление меняется по закону p(x,y) = p_k + Dp₁ ln((x-a)² + y²) + Dp₂ ln((x+a)² + y²). Определить скорость фильтрации в точке с координатами x = 20 м, y = 100 м, если Dp₁ = 4,5 МПа, Dp₂ = - 4,5 МПа, a = 100 м, проницаемости пласта 0,24 мкм², динамический коэффициент вязкости нефти μ = 12 мПа·с.

Задача 1.25

Определить значение числа Рейнольдса у стенки гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если известно, что эксплуатационная колонна перфорирована, на каждом погонном метре колонны прострелено 10 отверстий диаметром d_п = 10 мм, толщина пласта h = 15 м, проницаемость пласта k = мкм², пористость его m = 18%, коэффициент вязкости нефти μ = 4 мПа·с, плотность нефти ρ = 870 кг/м³ и дебит скважины составляет 140 м³/сут.

Date: 2015-10-19; view: 1850; Нарушение авторских прав