
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод Рунге-Кутта 4 порядка
|
|
Тамбов, 2010
Цель работы: Нахождение приближенного решения системы обыкновенных дифференциальных уравнений методом Рунге-Кутта 3 и 4 порядка и сравнение полученных результатов с решением, полученным аналитически.
Теоретическая часть
Согласно методу Рунге – Кутта 3 порядка, последовательные значения 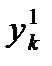 искомой системы дифференциальных уравнений определяются по формуле:
искомой системы дифференциальных уравнений определяются по формуле:
 , где
, где

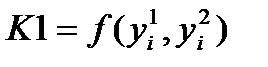


а последовательные значения 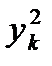 искомой системы дифференциальных уравнений определяются по формуле:
искомой системы дифференциальных уравнений определяются по формуле:
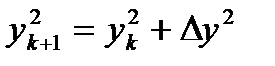 , где
, где 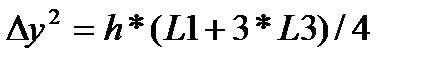
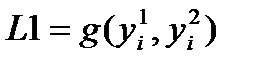

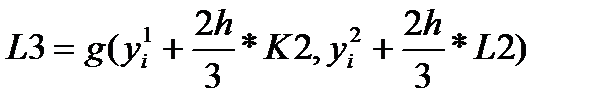
Метод Рунге-Кутта 4 порядка
Согласно методу Рунге – Кутта 4 порядка, последовательные значения 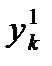 искомой системы дифференциальных уравнений определяются по формуле:
искомой системы дифференциальных уравнений определяются по формуле:  ,
,
где
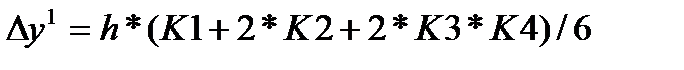
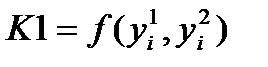
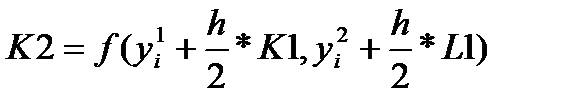
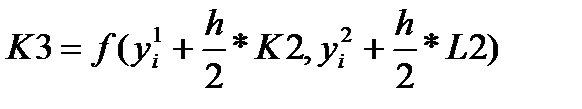
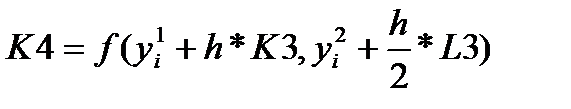
а последовательные значения 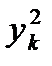 искомой системы дифференциальных уравнений определяются по формуле:
искомой системы дифференциальных уравнений определяются по формуле: 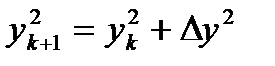 , где
, где

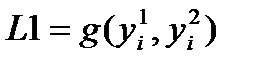

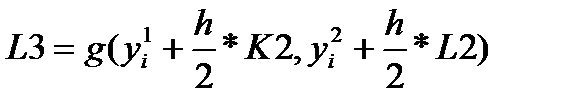

Date: 2015-10-19; view: 370; Нарушение авторских прав