
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторная работа №2
|
|
СТАТИСТИЧЕСКИЙ АНАЛИЗ РЯДА ДИНАМИКИ.
Цель работы – изучение статистических показателей анализа ряда динамики и выявление закономерностей их развития во времени.
Краткие теоретические сведения.
Динамический ряд представляет собой последовательность уровней, сопоставляя которые между собой, можно получить характеристику скорости и интенсивности развития явлений. В результате сравнения уровней получается система следующих абсолютных и относительных показателей динамики.
Цепной и базисный абсолютный прирост определяется по формулам: 
 (1)
(1)
 (2)
(2)
где  - уровень сравниваемого периода;
- уровень сравниваемого периода;  - уровень базисного периода;
- уровень базисного периода;  - уровень непосредственного предшествующего периода.
- уровень непосредственного предшествующего периода.
Цепной и базисный темпы роста рассчитывается по формулам:


, (3)
 , (4)
, (4)
Цепной и базисный темпы прироста определяются по формулам:


, (5)
 , (6)
, (6)
Абсолютное значение 1% прироста рассчитывается по формуле
 , (7)
, (7)
Для обобщающей характеристики динамики исследуемого явления определяются следующие средние показатели: средний уровень ряда, средний абсолютный прирост, средние темп роста и прироста. Для интервального ряда абсолютных показателей средний уровень за период определяется по формуле простой средней арифметической:
 , (8)
, (8)
где n – число уровней ряда.
Средний абсолютный прирост (или средняя скорость роста) рассчитывается как средняя арифметическая из показателей скорости роста за определенные промежутки времени.

 , (9)
, (9)
где  - цепной абсолютный прирост.
- цепной абсолютный прирост.
Средний темп роста вычисляется по формуле:
 , (10)
, (10)
где 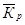 - средний коэффициент роста, который вычисляется по формуле средней геометрической из показателей цепных коэффициентов роста за отдельные периоды.
- средний коэффициент роста, который вычисляется по формуле средней геометрической из показателей цепных коэффициентов роста за отдельные периоды.
 , (11)
, (11)
где  - цепные коэффициенты роста. Средний коэффициент роста можно также определить по формуле
- цепные коэффициенты роста. Средний коэффициент роста можно также определить по формуле
 , (12)
, (12)
Средний темп прироста рассчитывается по формуле:

 , (13)
, (13)
Одной из задач, возникших при анализе рядов динамики, является выявление основной тенденции развития (тренда) изучаемого явления. Для того чтобы дать количественную модель, выражающую общую тенденцию изменений уровней динамического ряда во времени, используется метод аналитического выравнивания ряда динамики. Основным содержанием этого метода является то, что основная тенденция развития  рассчитывается как функция времени
рассчитывается как функция времени
 , (14)
, (14)
Определение теоретических (расчетных) уровней  производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда. В практике статистического изучения тренда наиболее часто применяют следующие функции:
производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда. В практике статистического изучения тренда наиболее часто применяют следующие функции:
1) Прямолинейная функция
 , (15)
, (15)
где а0 и а1 - параметры уравнения, t – обозначение времени.
2) Функция параболы второго порядка
 , (16)
, (16)
где  - параметры уравнения.
- параметры уравнения.
3) Функция параболы третьего порядка
 , (17)
, (17)
где 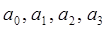 - параметры уравнения.
- параметры уравнения.
4) Показательная функция
 , (18)
, (18)
где 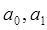 - параметры уравнения.
- параметры уравнения.
Одним из применяемых в практике статистического изучения тренда показателей адекватности математической функции является стандартная ошибка аппроксимации, которая рассчитывается по формуле:
 , (19)
, (19)
где  - теоретические и эмпирические уровни ряда. За наиболее адекватную принимается функция, стандартная ошибка аппроксимации которой имеет минимальное значение.
- теоретические и эмпирические уровни ряда. За наиболее адекватную принимается функция, стандартная ошибка аппроксимации которой имеет минимальное значение.
Под экстраполяцией понимается распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее. Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики, выступающего в качестве базы прогнозирования, сохраняется и в дальнейшем.
 Применение методов экстраполяции зависит от характера изменений в базисном ряду динамики и предопределяется постановкой задачи исследования. При экстраполяции уровней развития изучаемого явления на базе ряда динамики с постоянными абсолютными приростами
Применение методов экстраполяции зависит от характера изменений в базисном ряду динамики и предопределяется постановкой задачи исследования. При экстраполяции уровней развития изучаемого явления на базе ряда динамики с постоянными абсолютными приростами  применяется формула
применяется формула

 , (20)
, (20)
 где yn+l - экстраполируемый уровень, yn – конечный уровень базисного ряда, l – срок прогноза.
где yn+l - экстраполируемый уровень, yn – конечный уровень базисного ряда, l – срок прогноза.
При экстраполяции уровней изучаемого явления на базе ряда динамики со стабильными темпами роста (Трц = const) применяется формула

 , (21)
, (21)
При прогнозировании тренда изучаемого явления на основе аналитического выравнивания применяется адекватная трендовая модель.
Порядок выполнения работы.
I. Используя исходные данные, произвести интерполяцию уровней ряда по формулам (20) или (21). По полученным результатам рассчитать следующие абсолютные, относительные и средние показатели ряда динамики:
1) цепные и базисные абсолютные приросты,
2) цепные и базисные темпы роста,
3) цепные и базисные темпы прироста,
4) абсолютное содержание I% прироста,
5) средний уровень ряда,
6) средний абсолютный прирост,
7) средние темпы роста и прироста.
Результаты расчетов п. 1-4 представить в виде табл.I.
II. выявить основную тенденцию (тренд) изменения анализируемого показателя методом аналитического выравнивания. Для определения параметров математических функций при анализе тренда в рядах динамики используется способ отсчета времени от условного начала. Он основан на обозначении в рядах динамики показаний времени таким образом, чтобы åt=0. Это значительно упрощает расчеты.
Таблица I.
Результаты расчетов.
| год | Уровни ряда | Абсолютный прирост, ∆i | Темп роста, % (Тр) | Темп прироста (Тпр) % | Абсолютное содержание 1%-го прироста | |||
| Цепной | Базисный | Цепной | Базисный | Цепной | Базисный | |||
При использовании способа условного обозначения времени, когда åt=0, параметры математических функций определяются следующим образом:
а) для прямолинейной функции yt=a0+a1t (при åt=0)
a0=  ,
,  ,
,
где n – число членов ряда динамики.
Все суммы, необходимые для решения системы, берутся из табл. 2.
Таблица 2.
Расчетная таблица
| год | у | t | t2 | yt | yt |
| итого | åy | åt=0 | åt2 | åyt | åyt |
б) для параболы второго порядка 
(при åt=0). Все суммы, необходимые для решения системы, берутся из табл. 3.

Таблица 3.
Расчетная таблица
| год | y | T | t2 | t4 | yt | yt2 | yt |
| итого | åy | åt=0 | åt2 | åt4 | åyt | åyt2 | åyt |
в) для параболы третьего порядка 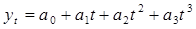
(при åt=0).
Все суммы, необходимые для решения системы, берутся из табл. 4.

Таблица 4.
Расчетная таблица
| Год | y | t | t2 | t4 | t6 | ty | t2y | t2y | yt |
| итого | åy | åt=0 | åt2 | åt4 | å t6 | åty | å t2y | åt3y | å yt |
г) для показательной функции yt=a0 a1t (при åt=0).
Все суммы, необходимые для решения системы, берутся из табл.5.

Таблица 5.
Расчетная таблица
| год | y | t | t2 | lgy | t lg y | yt |
| итого | åy | åt=0 | åt2 | å lg y | å t lg y | åyt |
Для решения вопроса, какая из этих моделей является наиболее адекватной, сравниваются их стандартные ошибки аппроксимации, для определения которых составляется матрица расчетных значений (табл. 6, 7)
Таблица 6.
Матрица определения s yt для прямолинейной функции и функции параболы второго порядка.
| год | t | Отклонение теоретических уровней yt i от фактических уровней yi | ||||
| Прямолинейная функция (15) | Парабола второго порядка (16) | |||||
| yti- yi | (yti- yi)2 | yti- yi | (yti- yi)2 | |||
| итого | åt=0 | å(yti- yi)2 | å(yti- yi)2 | |||
Таблица 7
Матрица определения syt для функции параболы третьего порядка и показательной функции.
| год | t | y | Отклонение теоретических уровней yti от фактических уровней yi | ||||||
| Парабола третьего порядка (17) | Показательная функция (18) | ||||||||
| yti- yi | (yti- yi)2 | yti- yi | (yti- yi)2 | ||||||
| итого | åt=0 | åy | å(yti- yi)2 | å(yti- yi)2 | |||||
За наиболее адекватную принимается функция, стандартная ошибка аппроксимации которой имеет наименьшее значение.
3.построить график зависимости изменения уровней ряда от времени для теоретических и эмпирических уровней.
4. Используя метод аналитического выравнивания, произвести экстраполяцию изучаемого явления.
Лабораторная работа № 3.
ИНДЕКСНЫЙ МЕТОД ФАКТОРНОГО АНАЛИЗА
Цель работы – определить и проанализировать степень влияния отдельных факторов на уровень совокупного финансового показателя.
Краткие теоретические сведения
Индексный метод факторного анализа применяется для оценки влияния на объемный показатель изменения факторов, его формирующих. Этот метод используется в тех случаях, когда связь между показателями можно выразить математическив виде уравнения связи, либо мультипликативного
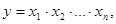
либо аддитивного

Вид функции, число переменных факторов (сомножителей или слагаемых) определяются логикой изучаемой связи.
При анализе динамики результативного экономического показателя индексный метод факторного анализа позволяет определить степень влияния на изменение этого показателя каждого из факторов, его составляющих. Для этого применяется принцип элиминирования –логический приём, используемый при изучении функциональной связи, при котором последовательно выделяется влияние одного фактора и исключается влияние всех остальных. При этом общий результат изменения этого объёмного экономического показателя представляет собой сумму изменений за счёт влияния всех исследуемых факторов, формирующих это влияние.
В данной работе приводится методика применения индексного метода факторного анализа для оценки влияния фактора, включенных в индексную модель на изменение общей рентабельности.
Общая рентабельность (Rб) определяется как отношение суммы балансовой (бухгалтерской) прибыли (Пб) к средней за период стоимости производимого капитала (КП).
 (1)
(1)
Этот показатель может быть выражен следующей мультипликационной индексной моделью:
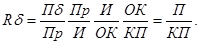 (2)
(2)
или в общем виде
y=abcd,
где y= 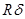 - уровень рентабельности;
- уровень рентабельности;  - коэффициент структуры прибыли;
- коэффициент структуры прибыли;  - рентабельность реализованной продукции;
- рентабельность реализованной продукции;  - число оборотов оборотного капитала, рассчитанное по полным затратам на реализованную продукцию;
- число оборотов оборотного капитала, рассчитанное по полным затратам на реализованную продукцию;  - доля оборотного капитала в общей стоимости производственного капитала.
- доля оборотного капитала в общей стоимости производственного капитала.
Влияние каждого фактора на изменение общей рентабельности покажет отношение отчетного уровня данного фактора к базовому и в относительном выражении это влияние определяется по следующей схеме индексов:
 (3)
(3)
Общее абсолютное изменение уровня общей рентабельности под влиянием вышеназванных факторов определяется как сумма влияния всех факторов по формуле:
 (4)
(4)
где  - влияние изменения структуры прибыли (фактора a).
- влияние изменения структуры прибыли (фактора a).
Определяется по формуле:
 (5)
(5)
где ∆ yb – влияние изменения рентабельности реализованной продукции (фактора b). Определяется по формуле:
∆ yb =  (6)
(6)
где ∆ yc – влияние изменения оборачиваемости нормируемого оборотного капитала (фактора с). Определяется по формуле:
 (7)
(7)
где ∆ yd - влияние изменения доли стоимости оборотного капитала в общей стоимости производственного капитала (фактора d). Определяется по формуле:
 (8)
(8)
Порядок выполнения работы.
1. Используя исходные данные прил. 3, определить величину каждого фактора, влияющего на изменение общей рентабельности для базового и отчётного периода.
2. Рассчитать абсолютные и относительные показатели динамики. Результаты расчетов оформить в виде таблицы.
3. Определить влияние каждого фактора на изменение общей рентабельности:
а) в относительном выражении (см. формулу (3));
б) в абсолютном выражении (см. формулы (4-8))
4. По результатам расчетов сделать выводы.
| ПОКАЗАТЕЛИ | Базовый период | Отчетный период | Абсолютное изменение | Относительное изменение |
| Балансовая прибыль, Пб Выручка от реализации, РП Издержки производства, И Прибыль от реализации, Пр Производственный капитал, КП Оборотный капитал, ОК Коэффициент структуры прибыли, a Рентабельность реализованной продукции, b Число оборотов оборотного капитала, с Доля оборотного капитала в общей стоимости производственного капитала, d Общая рентабельность, y |
Библиографический список
1. Елисеева И.И. Общая теория статистики: Учебник / И.И. Елисеева, М.М. Юзбашев; Под редакцией И.И. Елисеевой. – М.: Финансы и статистика, 2001.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. Москва: ИНФРА – М, 2000.
3. Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др. Статистика: Учебное пособие / Под ред. Ионина В.Г. Москва: ИНФРА – М, 2001.
4. Экономическая статистика. Учебник под ред. Иванова Ю.Н. Москва: ИНФРА – М, 2000.
5. Экономика и статистика фирм: Учебник / В.Е. Адамов, С.Д. Ильенкова, Т.П. Сиротина и др.; Под редакцией С.Д. Ильенковой. – М.: Финансы и статистика, 2001.
Приложение 1
Варианты заданий
| № предприятия | Среднегодовая стоимость основных средств, млн.р. | |||||||||||||||
| ВАРИАНТЫ ЗАДАНИЙ | ||||||||||||||||
| 7,6 | 3,4 | 1,6 | 4,0 | 12,7 | 3,5 | 5,8 | 12,8 | 6,3 | 4,5 | 5,0 | 6,0 | 8,0 | 3,0 | 3,5 | 7,0 | |
| 9,8 | 3,1 | 3,9 | 8,0 | 6,9 | 0,9 | 5,2 | 7,8 | 7,5 | 5,5 | 4,0 | 7,0 | 3,0 | 4,0 | 1,0 | 8,0 | |
| 3,3 | 3,5 | 3,3 | 5,1 | 7,3 | 1,0 | 3,8 | 0,8 | 6,6 | 9,0 | 3,0 | 4,0 | 2,0 | 2,0 | 3,0 | 9,0 | |
| 6,3 | 4,1 | 4,9 | 4,9 | 2,9 | 7,0 | 4,1 | 3,3 | 3,3 | 3,6 | 6,0 | 3,0 | 4,0 | 5,0 | 2,0 | 4,0 | |
| 4,0 | 5,8 | 3,0 | 6,3 | 4,5 | 4,5 | 5,6 | 4,3 | 4,0 | 3,6 | 4,0 | 9,2 | 1,0 | 6,0 | 5,0 | 5,0 | |
| 6,2 | 5,2 | 5,1 | 7,5 | 12,8 | 8,1 | 4,5 | 5,5 | 8,0 | 9,0 | 2,0 | 5,0 | 7,0 | 7,0 | 6,0 | 6,0 | |
| 5,0 | 3,8 | 3,1 | 6,6 | 7,8 | 6,3 | 4,2 | 4,3 | 5,1 | 4,5 | 7,0 | 7,0 | 9,0 | 8,0 | 7,0 | 7,0 | |
| 7,8 | 4,1 | 0,5 | 3,3 | 0,8 | 5,5 | 6,1 | 9,1 | 4,9 | 4,3 | 9,9 | 8,0 | 5,0 | 9,0 | 8,0 | 2,0 | |
| 2,7 | 5,6 | 3,1 | 6,7 | 4,1 | 6,6 | 6,5 | 12,7 | 6,7 | 7,2 | 9,0 | 9,9 | 9,9 | 9,0 | 2,0 | ||
| 4,5 | 5,6 | 3,4 | 4,3 | 1,0 | 2,0 | 6,9 | 3,4 | 8,1 | 3,0 | 2,0 | 9,9 | 5,0 | 9,9 | 9.8 | ||
| 7,2 | 4,2 | 3,5 | 3,3 | 5,5 | 1,6 | 6,4 | 7,3 | 3,3 | 2,0 | 8,0 | 2,0 | 2,0 | 6,0 | 4,0 | 1,0 | |
| 8,2 | 6,1 | 0,9 | 3,9 | 4,3 | 3,9 | 4,0 | 2,9 | 3,9 | 9,0 | 7,0 | 4,0 | 4,0 | 7,0 | 5,0 | 2,0 | |
| 7,8 | 6,5 | 1,0 | 4,1 | 9,1 | 3,3 | 8,0 | 4,5 | 4,1 | 3,6 | 5,0 | 3,0 | 5,0 | 4,0 | 6,0 | 3,0 | |
| 9,1 | 2,0 | 7,0 | 5,9 | 1,4 | 4,9 | 5,1 | 1,4 | 5,9 | 4,5 | 4,0 | 5,0 | 6,0 | 8,0 | 3,0 | 4,0 | |
| 6,2 | 6,4 | 4,5 | 6,4 | 7,6 | 3,0 | 4,9 | 7,6 | 6,4 | 5,4 | 2,0 | 9,0 | 7,0 | 9,0 | 4,0 | 5,0 | |
| 5,0 | 4,0 | 8,1 | 3,9 | 3,6 | 5,1 | 4,3 | 3,6 | 3,9 | 9,0 | 1,0 | 9,9 | 8,0 | 9,9 | 5,0 | 6,0 | |
| 6,7 | 8,0 | 6,3 | 5,6 | 4,4 | 3,1 | 5,8 | 4,4 | 5,6 | 0,9 | 4,0 | 1,6 | 9,0 | 4,0 | 6,0 | 6,0 | |
| 3,3 | 5,1 | 5,6 | 3,5 | 6,9 | 0,5 | 7,2 | 6,9 | 3,5 | 8,1 | 6,0 | 2,0 | 9,9 | 5,0 | 8,0 | 3,0 | |
| 8,0 | 4,9 | 6,6 | 3,0 | 4,6 | 3,1 | 6,6 | 4,6 | 3,0 | 5,4 | 7,0 | 3,0 | 3,0 | 6,0 | 9,0 | 2,0 | |
| 7,2 | 4,3 | 1,0 | 5,4 | 5,8 | 5,6 | 3,0 | 5,8 | 5,4 | 7,2 | 9,0 | 5,6 | 2,0 | 2,0 | 9,9 | 1,0 | |
| 4,5 | 5,8 | 4,7 | 2,0 | 11,7 | 6,8 | 6,7 | 11,7 | 2,0 | 2,7 | 9,9 | 6,0 | 3,8 | 4,0 | 9,9 | 1,5 | |
| 4,5 | 7,2 | 2,7 | 4,5 | 7,4 | 2,9 | 3,4 | 7,4 | 4,5 | 1,8 | 1,0 | 7,0 | 4,0 | 5,0 | 1,6 | ||
| 4,6 | 6,6 | 2,9 | 4,8 | 10,9 | 2,7 | 3,1 | 10,9 | 4,8 | 2,7 | 6,0 | 8,0 | 5,0 | 9,0 | 1,7 | ||
| 4,5 | 3,0 | 6,8 | 5,9 | 8,0 | 4,7 | 3,5 | 5,0 | 5,9 | 0,9 | 8,0 | 9,0 | 8,0 | 4,0 | 1,9 | ||
| 6,2 | 6,7 | 9,0 | 7,2 | 6,0 | 5,0 | 4,1 | 7,0 | 7,2 | 9,0 | 4,0 | 3,0 | 9,0 | 5,0 | 7,6 | 2,0 |
Приложение 2
Варианты заданий
| № пред прия тия | Объем выпуска товарной продукции, млн.р. | |||||||||||||||
| ВАРИАНТЫ ЗАДАНИЙ | ||||||||||||||||
| 11,0 | 3,5 | 1,5 | 4,2 | 16,0 | 3,0 | 7,5 | 15,0 | 8,0 | 5,0 | 4,5 | 4,8 | 5,6 | 3,0 | 3,0 | 6,5 | |
| 13,2 | 3,3 | 4,2 | 9,9 | 7,6 | 0,6 | 6,9 | 12,0 | 9,4 | 6,0 | 3,6 | 5,6 | 2,1 | 4,3 | 1,2 | 9,0 | |
| 3,8 | 3,5 | 4,5 | 9,8 | 11,2 | 1,1 | 4,3 | 0,7 | 9,9 | 2,7 | 3,6 | 1,9 | 2,5 | 3,0 | 9,9 | ||
| 4,9 | 4,5 | 4,4 | 5,3 | 3,2 | 7,5 | 5,9 | 5,3 | 3,4 | 4,0 | 5,9 | 2,4 | 2,8 | 5,0 | 2,2 | 5,0 | |
| 3,7 | 7,5 | 2,0 | 8,0 | 4,9 | 5,6 | 4,8 | 4,8 | 4,2 | 4,0 | 3,6 | 8,0 | 0,8 | 5,4 | 4,8 | 6,0 | |
| 9,7 | 6,9 | 4,2 | 9,4 | 15,0 | 7,6 | 5,8 | 5,7 | 9,9 | 8,1 | 4,0 | 4,9 | 7,2 | 6,3 | 7,0 | ||
| 3,8 | 4,3 | 4,0 | 12,0 | 6,0 | 4,6 | 4,8 | 5,8 | 5,0 | 6,3 | 5,6 | 6,0 | 7,8 | 7,1 | 8,0 | ||
| 10,6 | 5,9 | 0,4 | 3,9 | 0,7 | 8,4 | 8,4 | 10,9 | 5,3 | 7,0 | 9,0 | 6,4 | 3,5 | 9,0 | 8,0 | 3,0 | |
| 2,9 | 4,8 | 3,6 | 7,0 | 5,3 | 6,5 | 7,3 | 16,6 | 7,0 | 8,0 | 9,9 | 6,3 | 7,7 | 8,9 | 3,5 | ||
| 15,3 | 5,8 | 7,9 | 2,9 | 4,8 | 0,9 | 2,1 | 7,6 | 2,9 | 9,0 | 2,7 | 1,8 | 7,0 | 4,9 | 1,5 | ||
| 7,5 | 4,6 | 3,0 | 3,3 | 5,7 | 1,5 | 7,8 | 11,2 | 3,3 | 1,0 | 7,2 | 1,0 | 1,4 | 6,2 | 4,5 | 1,0 | |
| 10,9 | 8,4 | 0,6 | 5,4 | 4,8 | 4,2 | 4,2 | 3,2 | 5,4 | 9,0 | 6,3 | 3,2 | 2,8 | 7,5 | 5,8 | 2,4 | |
| 10,6 | 7,3 | 1,1 | 5,0 | 10,9 | 4,5 | 4,9 | 5,0 | 4,0 | 4,5 | 2,9 | 3,5 | 3,5 | 6,5 | 4,0 | ||
| 11,9 | 2,1 | 7,5 | 7,0 | 1,2 | 4,4 | 5,8 | 1,2 | 7,0 | 5,0 | 3,6 | 4,0 | 4,2 | 8,3 | 3,5 | 5,0 | |
| 9,8 | 7,8 | 5,6 | 7,9 | 8,6 | 2,0 | 5,3 | 8,6 | 7,5 | 6,0 | 1,8 | 7,2 | 4,9 | 9,2 | 4,3 | 6,0 | |
| 7,7 | 4,2 | 7,6 | 6,4 | 3,6 | 4,2 | 4,9 | 3,6 | 6,4 | 0,9 | 8,0 | 8,0 | 5,0 | 5,0 | |||
| 8,8 | 6,0 | 4,6 | 6,7 | 4,0 | 6,0 | 6,7 | 4,6 | 8,1 | 3,6 | 0,8 | 6,3 | 4,5 | 6,5 | 6,5 | ||
| 2,8 | 5,8 | 8,4 | 4,1 | 8,4 | 0,4 | 8,4 | 4,1 | 9,0 | 5,4 | 1,6 | 7,0 | 5,3 | 8,5 | 4,0 | ||
| 9,9 | 5,3 | 6,5 | 3,8 | 6,9 | 3,6 | 6,9 | 6,9 | 3,8 | 6,0 | 6,3 | 2,4 | 3,0 | 5,8 | 9,1 | 3,0 | |
| 8,0 | 4,9 | 0,9 | 8,5 | 6,7 | 7,9 | 3,5 | 6,7 | 8,6 | 8,0 | 8,1 | 4,0 | 4,0 | 2,5 | 9,8 | 1,5 | |
| 4,7 | 6,0 | 4,5 | 1,8 | 12,9 | 6,9 | 7,2 | 13,6 | 1,8 | 3,0 | 9,0 | 4,8 | 1,5 | 3,5 | 9,7 | 2,0 | |
| 4,8 | 9,4 | 2,3 | 4,6 | 10,4 | 3,2 | 3,5 | 10,0 | 4,6 | 2,0 | 0,9 | 6,3 | 1,7 | 5,3 | 9,9 | 1,8 | |
| 6,6 | 6,9 | 3,2 | 5,2 | 13,5 | 2,3 | 3,3 | 5,2 | 3,0 | 5,0 | 7,2 | 3,0 | 8,9 | 2,0 | |||
| 8,2 | 3,5 | 6,9 | 9,0 | 12,2 | 4,5 | 3,5 | 7,0 | 9,0 | 1,8 | 6,3 | 7,5 | 5,6 | 4,5 | 2,2 | ||
| 9,8 | 7,2 | 9,9 | 8,6 | 9,0 | 5,1 | 4,5 | 8.5 | 8,6 | 9,9 | 3,0 | 2,4 | 6,8 | 5,5 | 7,5 | 3,0 |
Приложение 3.
Варианты заданий
| Варианты | ПОКАЗАТЕЛИ | |||||
| Период | Пб | РП | И | ПК | ОК | |
| Базовый Отчетный | 22800 24275 | 19000 20399 | 43700 46650 | |||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный | ||||||
| Базовый Отчетный |
Date: 2015-10-19; view: 519; Нарушение авторских прав