
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторная работа № 1
|
|
СТАТИСТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА В ЭКОНОМИКЕ
Методические указания к лабораторным и самостоятельным работам
ПЕНЗА 2002
Рассмотрен ряд методов статистического анализа, применяемых в статистике: методы сводки, группировки, средних величин, показателей вариации, методы анализа динамических рядов и индексного факторного анализа.
Методические указания подготовлены на кафедре «Экономика, финансы и менеджмент» Пензенского государственного университета и предназначены для студентов экономических специальностей, изучающих дисциплину «Статистика».
Составители: Д.В. Григорьев, Э.Д. Ежова.
Рецензент:
Лабораторная работа № 1.
СТАТИСТИЧЕСКАЯ СВОДКА И ГРУППИРОВКА. ВЫЯВЛЕНИЕ ВЗАИМОСВЯЗИ МЕЖДУ ИЗУЧАММЫМИ ПРИЗНАКАМИ.
Цель работы - использование метода группировки для анализа и выявления взаимосвязи между факторными и результативными признаками изучаемого явления.
Краткие теоретические сведения.
Первой ступенью систематизации и обобщения данных статистического наблюдения является статистическая сводка.
Сводка представляет собой комплекс статистических операций по обобщению конкретных единичных данных, образующих совокупность с целью выявления типичных черт и закономерностей, присущих данному явлению. Статистическая сводка состоит в том, что первичные материалы, полученные в результате наблюдения, заносятся в таблицы, подсчитываются итоговые показатели. В дальнейшем на основе сводных итогов вычисляют средние и относительные величины. Различают простую сводку (только для подсчета итоговых показателей) и статистическую группировку.
Под группировкой в статистике понимают разделение статистической совокупности на группы однородные в каком-либо существенном отношении и характеристику выделенных групп системой показателей в целях выделения типов явлений, изучения их структуры и взаимосвязей. С помощью метода группировок решаются три основные задачи: выделение социально-экономических типов явлений, изучение структуры однотипных совокупностей, исследование связей и зависимостей между признаками исследуемого явления. Согласно задачам, группировки соответственно делятся на три вида: типологические, структурные и аналитические.
В основу типологических и структурных группировок могут быть доложены атрибутивные и количественные признаки.
Атрибутивный признак - это качественный признак группировки, который не имеет количественного выражения.
При использовании количественных признаков в группировках возникают проблемы определения числа групп и величины интервала.
При равных интервалах для определения числа групп используется формула Стерджесса:
n = 1 + 3,322 lg N, (1)
где n - число групп; N - численность единиц совокупности. Величина интервала определяется делением размаха вариации на число групп:
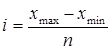 (2)
(2)
где xmax и xmin – максимальное и минимальное значения признака; n - число групп.
Как было сказано выше, основной задачей аналитической группировки является выявление взаимосвязи между изучаемыми явлениями и признаками их характеризующими. Для использования метода аналитической группировки прежде всего нужно определить факторные и результативные признаки изучаемых явлений.
Факторные - это признаки, оказывающие влияние на другие, связанные с ними признаки.
Результативные - признаки, которые изменяются под влиянием факторов. Взаимосвязь проявляется в том, что с изменением значения факторного признака систематически возрастает или убывает значение результативного признака.
Далее определяется число групп, величина интервала и составляется макет рабочей таблицы.
Таблица I
Макет рабочей таблицы
| Номер группы | Группы предприятий по размеру среднегодовой стоимости основных средств, млн р. | Номер предприятия | Среднегодовая стоимость основ- ных средств, млн р. | Объем выпуска товарной продукции, млн р. |
Групповые данные рабочей таблицы заносятся в сводную групповую таблицу, характеризующую зависимость между среднегодовой стоимостью основных средств и объемом товарной продукции. Обе таблицы должны быть оформлены  статистически грамотно: иметь заглавие, наименование подлежащего, сказуемого, единицы измерения показателей, итоговые общие и средние показатели.
статистически грамотно: иметь заглавие, наименование подлежащего, сказуемого, единицы измерения показателей, итоговые общие и средние показатели.
Таблица 2
Макет сводной групповой таблицы
| Группы предприятий по размеру среднегодовой стоимости основных средств, млн. р. | Число предприятий | Среднегодовая стоимость основных средств, млн.р. | Объем выпуска товарной продукции, млн.р. | Фондоотдача | ||
| всего | в среднем на одно предприятие | всего | в среднем на одно предприятие | |||
Существует много типов средних величин. Вид и форма средней выбирается исходя из имеющихся исходных данных.
В данной работе для определения средних величин используется средняя арифметическая простая:
 , (3)
, (3)
где x - величина признака,  - количество признаков.
- количество признаков.
В статистике употребляются также ещё две разновидности средних - мода и медиана.
Модой - называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряде распределения это будет варианта с наибольшей частотой.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд на две равные части. Определить моду и медиану в дискретном вариационном ряде несложно. В интервальном вариационном ряде мода и медиана определяются по формулам (4) и (5):
 ,
,  (4)
(4)
где xмо - начальное значение интервала, содержащего моду; iмо - величина модального интервала; fмо+1 - частота интервала, следующего за модальным; fмо-1 - частота интервала, предшествующего модальному, fмо – частота модального интервала.
 , (5)
, (5)
где xме - начальное значение медианного интервала; 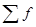 - сумма частот ряда; Sме-1 - сумма накопленных частот в интервалах, предшествующих медианному; fме - частота медианного интервала.
- сумма частот ряда; Sме-1 - сумма накопленных частот в интервалах, предшествующих медианному; fме - частота медианного интервала.
Средние величины дают обобщающую характеристику всей совокупности изучаемого явления. Однако они не дают никакого представления о степени колеблемости (вариации) величины изучаемого признака.
Для изучения вариации признака в совокупности применяются различные обобщающие показатели, к которым относятся: размах вариации - R, среднее абсолютное отклонение -  , среднее квадратическое отклонение - σ; дисперсия –σ2; коэффициент вариации - V.
, среднее квадратическое отклонение - σ; дисперсия –σ2; коэффициент вариации - V.
Размах вариации - это разность между максимальным и минимальным значениями признака
R = xmax –xmin (6)
Размах вариации характеризует пределы изменения варьирующего признака.
Среднее абсолютное отклонение есть среднее арифметическое из абсолютных отклонений индивидуальных значений признака от общей средней. В зависимости от исходных данных среднее абсолютное отклонение определяется по формулам:
 ,(7)
,(7)
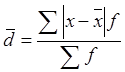 , (8)
, (8)
где  - средняя величина; f - частота повторений отдельных значений признака.
- средняя величина; f - частота повторений отдельных значений признака.
Среднее квадратическое отклонение простое определяется по формуле:

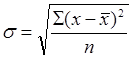 ,(9)
,(9)
Если определенные значения признака в изучаемой совокупности повторяются, то находят среднее взвешенное квадратическое отклонение по формуле:
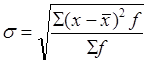 (10)
(10)
Дисперсия есть средняя арифметическая из квадратов отклонений индивидуальных значений признаков от средней. В зависимости от исходных данных определяется дисперсия простая (11) и дисперсия взвешенная (12).
 (11)
(11)
 (12)
(12)
Для исчисления дисперсии удобно пользоваться формулой (l3), из которой следует, что дисперсия равна разности средней из квадратов и квадрата средней.
 (13)
(13)
Коэффициент вариации - это отношение среднего квадратического отклонения к средней арифметической.
 , (14)
, (14)
Коэффициент вариации является показателем относительной вариации признака в совокупности. Его используют так же как характеристику однородности совокупности.
Совокупность считается однородной, если коэффициент вариации не превышает 33 %.
Если совокупность разбита на группы по изучаемому признаку, то для оценки влияния различных факторов, определяющих вариацию индивидуальных значений признака, общая дисперсия раскладывается на составляющие: среднюю из внутригрупповых дисперсий  и межгрупповую дисперсию
и межгрупповую дисперсию  .
.
Средняя из внутригрупповых дисперсий определяется по формуле (15) и характеризует ту часть вариации результативного признака, которая обусловлена действием случайных причин.
 , (15)
, (15)
где 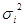 - внутригрупповая дисперсия, измеряющая вариацию признака внутри группы. Определяется по формулам:
- внутригрупповая дисперсия, измеряющая вариацию признака внутри группы. Определяется по формулам:
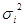
 ,
,  (16)
(16)
или
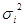
 , (17)
, (17)
где xi - отдельные значения признака внутри группы,  - групповые средние.
- групповые средние.
Межгрупповая дисперсия измеряет вариацию групповых средних вокруг общей средней и определяется по формуле:
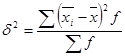 (18)
(18)
Межгрупповая дисперсия характеризует ту часть вариации результативного признака, которая складывается под влиянием изменения признака - фактора, положенного в основу группировки.
Между указанными видами дисперсий существует определенное соотношение:
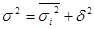 (19)
(19)
т.е. общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий. Это и есть правило сложения дисперсий.
Применение этого правила к методу аналитических группировок позволяет определить степень тесноты связи между результативным признаком и признаком - фактором, лежащим в основе группировки.
Для этого сначала определяется коэффициент детерминации 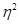 , который показывает, какую часть вариации изучаемого признака составляет вариация межгрупповая, т.е. обусловленная группировочным признаком.
, который показывает, какую часть вариации изучаемого признака составляет вариация межгрупповая, т.е. обусловленная группировочным признаком.
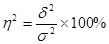
 (20)
(20)
Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением.
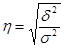 (21)
(21)
Корреляционное отношение характеризует степень тесноты связи между группировочным (факторным) и результативным признаками. Его значения находятся в пределах от 0 до 1. Приη= 0 - связь отсутствует, т.е. изменение факторного признака, положенного в основу группировки, не оказывает никакого влияния на результативный признак. Если η от 0,1 до 0,3 - то связь слабая, η - от 0,4 до 0,7 - связь умеренная, η - от 0,8 до 0,9 - связь тесная; при η = 1 - связь функциональная.
Порядок выполнения работы
Имеются следующие отчетные данные по 25 предприятиям одной из отраслей промышленности.
1. С целью изучения зависимости между среднегодовой стоимостью основных средств и объемом выпуска товарной продукции, используя исходные данные прил. 1 и 2, произвести группировку предприятий по среднегодовой стоимости основных средств, образовав пять групп предприятий с равными интервалами. По каждой группе и совокупности предприятий определить:
а) число предприятий;
б) среднегодовую стоимость основных средств - всего и в среднем на одно предприятие;
в) стоимость товарной продукции - всего и в среднем на одно предприятие;
г) стоимость товарной продукции на один рубль основных средств (фондоотдачу).
Результаты представить в виде таблицы, дать их краткий анализ.
По сгруппированным данным определить моду и медиану среднегодовой стоимости основных средств.
2. Вычислить относительные показатели структуры среднегодовой стоимости основных средств и объема товарной продукции в общем итоге всей совокупности предприятий для каждой из пяти образованных групп.
3. Рассчитать показатели вариации объема товарной продукции:
а) размах вариации;
б) среднее линейное отклонение;
в) общую дисперсию;
г) среднее квадратическое отклонение и коэффициент вариации;
д) общую дисперсию, используя правило сложения дисперсий. По результатам расчетов сделать краткие выводы.
4. Для изучения тесноты связи между объемом товарной продукции на одно предприятие (результативный признак - y) и их оснащенностью предприятий основными средствами (факторный признак – x), определить коэффициент детерминации и эмпирическое корреляционное отношение. Проанализировать полученные результаты. Сделайте краткие выводы.
Пример выполнения работы
Таблица 3
Исходные данные
| Номер предприятия | Среднегодовая стоимость основных средств, млн.р. | Объем выпуска товарной продукции, млн. р. |
| 6,9 8,9 3,0 5,7 3,7 5,6 4,5 7,1 2,5 10,0 6,5 7,5 7,1 8,3 5,6 4,5 6,1 3,0 6,9 6,5 4,1 4,1 4,8 4,1 5,6 | 3,5 4,5 3,4 8,8 3,5 9,6 2,5 13,9 6,8 9,9 9,6 10,8 8,9 7,0 8,0 2,5 9,2 6,9 4,3 4,4 6,0 7,5 8,9 |
1. Для применения метода аналитической группировки определяем величину интервала по формуле (2) и составляем рабочую таблицу 4 (см.табл. 1).
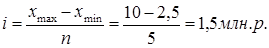
Таблица 4
Рабочая таблица
| Номер группы | Группы предприятий по среднегодовой стоимости основных средств, млн.р. | Номер предприятия | Среднегодовая стоимость основных средств, млн.р. | Объем выпуска товарной продукции, млн.р. |
| 2,5 - 4 | 3,0 3,7 2,5 3,0 | 3,5 3,4 2,6 2,5 | ||
| Итого | 12,2 | |||
| 4 – 5,5 | 4,5 4,5 4,1 4,1 4,8 4,1 | 3,5 4,3 4,4 6,0 7,5 | ||
| Итого | 25,5 | 32,7 | ||
| 5,5 - 7 | 6,9 5,7 5,6 6,5 5,6 6,1 6,9 6,5 5,6 | 10,0 4,5 8,8 6,8 8,9 8,0 9,2 6,9 8,9 | ||
| Итого | 55,4 | |||
| 7 – 8,5 | 7,1 7,5 7,1 8,3 | 9,6 9,9 9,6 10,8 | ||
| Итого | 39,9 |
Окончание табл. 4
| Номер группы | Группы предприятий по среднегодовой стоимости основных средств, млн.р. | Номер предприятия | Среднегодовая стоимость основных средств, млн.р. | Объем выпуска товарной продукции, млн.р. |
| 8,5 – 10 | 8,9 | 13,9 | ||
| Итого | 18,9 | 25,9 |
Далее групповые данные рабочей таблицы заносятся в сводную групповую таблицу (см. табл. 2).
Аналитическая группировка
Таблица 5
Зависимость объема выпуска товарной продукции
от среднегодовой стоимости основных средств
| Группы предприятий по среднегодовой стоимости основных средств, млн.р. | Число пред- прия- тий | Среднегодовая стоимость ос- новных средств, млн. р. | Объем выпуска товарной про- дукции, млн р. | Фондо- отдача | ||
| всего | в среднем на одно предприя- тие | всего | в среднем на одно предприя- тие | |||
| 2,5 – 4 4 – 5,5 5,5 – 7 7 – 8,5 8,5 – 10 | 12,2 25,5 55,4 18,9 | 3,05 4,25 6,15 7,5 9,45 | 32,7 39,9 25,9 | 5,45 9,97 12,95 | 0,98 1,28 1,30 1,33 1,37 | |
| Итого: | 5,68 | 182,5 | 7,3 | 1,28 |
По формулам (4) и (5) определяем моду и медиану среднегодовой стоимости основных средств.



2. Для изучения структуры среднегодовой стоимости основных средств и объема товарной продукции, используя данные рабочей табл. 4, произведем структурную группировку по среднегодовой стоимости основных средств (табл. 6).
Таблица 6
Структурная группировка заводов
по среднегодовой стоимости основных средств
| Группы предприятий по среднегодовой стоимости основных средств, млн. р. | Предприятия | Среднегодовая стоимость основ- ных средств, млн.р. | Объем выпуска товарной про- дукции, млн.р. | |||
| число единиц | % к итогу | млн.р. | % к итогу | млн.р. | % к итогу | |
| 2,5 – 4 4 – 5,5 5,5 -7 7 – 8,5 8,5 - 10 | 12,2 25,5 55,4 30,0 18,9 | 8,6 17,9 39,1 21,1 13,3 | 32,7 39,9 25,9 | 6,6 17,9 39,4 21,9 14,2 | ||
| Итого: | 182,5 |
3. Определяем показатели вариации объема товарной продукции.
Согласно формуле (6) размах вариации рассчитывается следующим образом:

По формулам (7), (9), (11), используя итоговые результаты табл. 7, определяем среднее линейное отклонение  ,дисперсию
,дисперсию  и среднее квадратическое отклонение
и среднее квадратическое отклонение 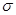 .
.
 |
Коэффициент вариации определяем по формуле (14)
Nbsp; Таблица 7
Расчетная таблица
| Номер предприятия | Объем выпуска товарной продукции,млн.р. |  
| 
|
| 3,5 4,5 3,4 8,8 3,5 9,6 2,6 13,9 6,8 9,9 9,6 10,8 8,9 7,0 8,0 2,5 | 2,7 4,7 3,8 2,8 3,9 1,5 3,8 2,3 4,7 6,6 0,5 2,6 2,3 3,5 1,6 0,3 0,7 4,8 | 7,29 22,09 14.44 7,84 15,21 2,25 14,44 5,29 22,09 43,56 0,25 6,76 5,29 12,25 2,56 0,09 0,49 23,04 |
Окончание табл. 7
| Номер предприятия | Объем выпуска товарной продукции, млн.р. | 
| 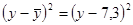
|
| 9,2 6,9 4,3 4,4 6,0 7,5 8,9 | 1,9 0,4 3,0 2,9 1,3 0,2 1,6 | 3,61 0,16 8,41 1,69 0,04 2,56 | |
| Итого | 182,5 | 64,4 | 230,7 |
Для того чтобы определить общую дисперсию по правилу сложения дисперсий, необходимо определить межгрупповую и среднюю из внутригрупповых дисперсий.
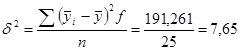 |
По формуле (18) рассчитываем межгрупповую дисперсию. Промежуточные расчеты приведены в табл. 8.
Таблица 8
Расчетная таблица
| Группы предприятий по среднегодовой стоимости ОС, млн.р. | Число пред- приятий, | Объем выпуска товарной продукции в среднем на одно предприятие, млн. р. |

|

|

|
| 2,5 – 4 4 – 5,5 5,5 – 7 7 – 8,5 8,5 – 10 | 5,45 9,97 12,95 | 4,3 1,85 0,7 2,67 5,65 | 18,49 3,422 0,49 7,129 31,922 | 73,96 20,53 4,41 28,516 63,845 | |
| Итого | 191,261 |
Внутригрупповые дисперсии определяем по формуле (15). Для первой группы внутригрупповая дисперсия определяется следующим образом:
 |
Аналогично определяются внутригрупповые дисперсии для последующих четырех групп. Они будут равны:
 .
.
 |
По формуле (17) рассчитываем среднюю из внутригрупповых дисперсий
Определяем общую дисперсию по формуле (19)
 |
4. Для изучения степени тесноты связи между объемом товарной продукции на одно предприятие и среднегодовой стоимостью основных средств определяется эмпирическое корреляционное отношение по формуле (21). Для этого сначала рассчитывается коэффициент детерминации по формуле (20):
 |
Тогда эмпирическое корреляционное отношение составит:
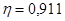 .
.
Date: 2015-10-19; view: 582; Нарушение авторских прав