Лабораторна робота №3 (4)

ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ МАЯТНИКА ОБЕРБЕКА

Мета роботи. Визначити момент інерції маятника Обербека; провести перевірку основного рівняння динаміки обертального руху.

Прилади і приладдя: хрестоподібний маятник Обербека, набір різноваг, вертикальна масштабна лінійка, електричний секундомір, штангенциркуль.

Матеріал, який необхідно засвоїти перед виконанням роботи: 1) Рух матеріальної точки по колу та його характеристики. 2) Другий закон Ньютона. 3) Маса і сила. 4) Основний закон динаміки обертального руху. 5) Енергія. 6) Потенціальна і кінетична енергія. 7) Закон збереження енергії.

Література

1. Грабовский Р.И. Курс физики: Учеб. пособие для с.-х. ин-тов. – М., 1979. – 552 с.

2. Розумнюк В.Т., Якименко І.Л. Фізика. Основні поняття, явища і закони. – Біла Церква, 2004. – 71 с.

Теоретичні відомості

При обертальному русі твердого тіла навколо деякої нерухомої осі його точки описують кола, центри яких лежать на цій осі (рис. 3.1).

Обертальний рух твердого тіла є одним із видів механічного руху, що значною мірою визначає закони дії різноманітних технічних пристроїв, опорно-рухової системи людини, тварини. Прикладами частин тіла людини і тварини що обертаються є: плечоліктеві, зап’ястні і фалангові з’єднання, атлантопотиличніі й епістрофоатлантові зчленування тощо. Це свідчить про важливість вивчення законів обертання і вміння визначати характеристики обертального руху тіл і їх частин. Однією із таких характеристик є момент інерції.

Зручною абстрактною моделлю для встановлення законів динаміки обертання є абсолютно тверде тіло.

Абсолютно твердим називається таке тіло, відстань між будь-якими точками якого незмінна.

Кожній точці відповідає маса m і радіус r кола, по якому вона рухається.Маса тіла (математичної точки), як відомо, характеризує його інертність при поступальному русі. У випадку обертального руху мірою інертності є момент інерції тіла (матеріальної точки).

Рис. 3.1.

Моментом інерції І матеріальної точки, що обертається навколо нерухомої осі, називають добуток її маси на квадрат радіуса r кола, по якому рухається точка:

І = mr². (1)

Із формули (1) випливає одиниця вимірювання І – кг·м².

Момент інерції тіла, що обертається, дорівнює сумі моментів інерції всіх матеріальних точок, з яких складається тіло, тобто:

,

де і – номер матеріальної точки, n – число точок.

Величина моменту інерції тіла залежить від його маси, форми і положення відносно осі обертання. Для однорідних тіл правильної геометричної форми значення І знаходять за формулами, які отримуються елементарним чином (дивися підручник), а для неоднорідних тіл неправильної форми – експериментальним шляхом. Останнє й необхідно зробити в цій роботі.

Під дією обертальної сили тіло набуває кутового прискорення β. Зв’язок між кутовим прискоренням і моментом обертальної сили та моментом інерції тіла виражається основним рівнянням обертального руху, яке є аналогом другого закону Ньютона для поступального руху ().

Кутове прискорення β, з яким рухається тіло під дією обертальної сили, прямо пропорційне моменту обертальної сили М і обернено пропорційне моменту інерції тіла І.

або М = Іβ. (2)

Моментом обертальної сили називають добуток обертальної сили F на радіус кола R, яке описується точкою прикладання сили.

М = F·R.

Одиниця вимірювання М – Н·м.

Опис установки і виведення робочих формул

У цій роботі визначення моменту інерції і перевірка основного рівняння динаміки обертального руху проводить-ся на прикладі маятника Обербека.

Маятник Обербека являє собою хрестовину, що складається з 4 стержнів із поділками, що кріпляться до втулки з віссю (рис. 3.2). На стержнях кріпляться грузи з однаковою масою, які можуть знаходиться на різних відстанях від осі обертання. На вісь обертання маятника насаджені два легких шківа з різними радіусами. На той чи інший шків намотується тонка нитка, до вільного кінця Рис. 3.2.

якої кріпиться груз. Під дією притягання цього груза до Землі нитка розмотується і маятник рівноприскорено обертається. Довжина нитки повинна бути такою, щоб при її повному змотуванні зі шківа груз ударив по кнопці кінцевого вимикача електричного секундоміра.

Робочу формулу для визначення моменту інерції маятника Обербека отримаємо, користуючись законом збереження енергії.

У верхньому положенні груз m має потенціальну енергію mgh, де g – прискорення вільного падіння тіл, h – висота, на яку піднятий груз. При падінні грузу його потенціальна енергія переходить у кінетичну енергію поступального руху грузу, в кінетичну енергію обертального руху маятника і витрачається на роботу А з подолання сил тертя. Силу тертя в умовах цього експерименту можна вважати сталою, тому поступальний рух грузу і обертання маятника будуть рівноприскореними.

У цьому випадку закон збереження енергії має вигляд:

, (3)

де v – швидкість падіння грузу в момент його удару по кнопці, ω – кутова швидкість обертання в цей момент.

Нехай робота з подолання тертя за один оберт А₁, а число обертів за часt₁від початку руху грузу до моменту його дотикання до кнопки n₁, тоді:

А = А₁n_1. (4)

В момент дотикання грузом підставки нитка повністю змотується зі шківа (петля нитки сповзає зі шпильки на шківі) й маятник продовжує обертатися деякий час, витрачаючи запас кінетичної енергії на подолання сили тертя.

Якщо після удару хрестовина зробила n₂ обертівдо повної зупинки, то:

= А₁ n₂.

Звідси:

А₁ = . (5)

Підставивши формулу (5) у формулу (4), отримаємо:

. (6)

З урахуванням формул (5) і (6) рівняння (3) приймає вигляд:

. (7)

У верхньому положенні груза лінійна швидкість v дорівнює нулю, а у нижньому положенні v = v _t. Оскільки рух груза рівноприскорений, то:

.

Окрім цього, і ; з іншого боку v = ωr, тоді , звідси:

, (8)

де r – радіус шківа.

Підставляючи формулу (8) у формулу (7), враховуючи, що , отримуємо:

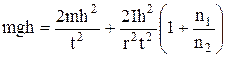, (9)

або:

.

Звідси момент інерції І:

(10)

Date: 2015-10-19; view: 657; Нарушение авторских прав