Метод Плакетта – Бермана

При выборе варьируемых переменных часто встает проблема определения факторов и их количества, влияющих на функцию цели. В этих условиях неопределенности предполагают возможные переменные, которые могут оказывать такое влияние. При этом, если использовать полный факторный план, то необходимо выполнить большое количество опытов. Для проведения таких опытов потребуется много времени и затрат средств. Например, для 16 факторов, варьируя переменные на двух уровнях необходимо провести опытов. Плакетт и Берман предложили планы эксперимента при которых оказалось возможным сократить число опытов до числа переменных плюс один.

В таблице 3.1. приведены / / первые строки матриц планов, содержащих от 8 до 72 опытов. Факторы варьируются на уровнях +1 (+) и -1 (-). Полные матрицы планов конструируются следующим образом: исходя из заданной первой строки, вторую и последующие строки получают путем сдвига всех элементов предыдущей строки на одну позицию вправо (или влево) и перестановки последнего (первого) элемента на первую (последнюю) позицию. Этот процесс повторяется раз. Последняя строка плана состоит только из элементов -1(-). Матрица плана имеет размерность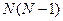

Таблица 3.1

Планы Плакетта-Бермана

N=8 + + + - + - -

N=12 + + - + + + - - - + -

N=16 + + + + - + - + + - - + - - -

N=20 + + - - + + + + - + - + - - - - + + -

N=24 + + + + + - + - + + - - + + - - + - + - - - -

Пример построения плана Плакетта-Бермана.

Чтобы получить план Плакетта- Бермана для выбирается первая строка плана и применяется (таблица 3.2) сформулированное правило.

Обработка результатов эксперимента

После реализации плана эксперимента производится обра­ботка его результатов, которая состоит из следующих операций:

1. Расчет эффектов отдельных факторов.

Расчет коэффициентов проводится путем вычисления разности между суммами значений целевой функции для фактора на уровнях +1 и —1, поде­ленной на N/4.

(3.3)

Из матрицы плана следует, что оценки эффектов могут быть рассчитаны независимо друг от друга (свойство ортогональности)

Таблица 3.2

N

+

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

+

+

-

+

+

-

-

+

-

-

-

+

+

+

+

-

-

+

+

-

-

+

-

-

-

+

+

+

+

-

+

+

+

-

-

+

-

-

-

+

+

+

+

-

+

-

+

-

-

+

-

-

-

+

+

+

+

-

+

-

+

-

-

+

-

-

-

+

+

+

+

-

+

-

+

+

-

+

-

-

-

+

+

+

+

-

+

-

+

+

-

+

-

-

-

+

+

+

+

-

+

-

+

+

-

-

-

-

-

+

+

+

+

-

+

-

+

+

-

-

+

-

-

+

+

+

+

-

+

-

+

+

-

-

+

-

-

+

+

+

+

-

+

-

+

+

-

-

+

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

2. Проверка значимости параметров.

Для выявления существенных факторов используется кри­терий и проверяется условие

(3.4)

где —критическое значение t - распределения для уровня зна­чимости степеней свободы; оценка дисперсии коэффициента . Дисперсия ошибок наблюдений оценивается с помощью спе­циальных экспериментов, например дублированием наблюдений или введением в план фиктивных факторов от . Если, например, план строится для анализа 12 факторов, то можно добавить к нему 3 фиктивных фактора и применить план типа N = 16.

Эффекты этих фиктивных переменных будут равны нулю лишь в том случае, если не имеется в0здействия на целевую функцию и измере­ния являются абсолютно точными. Поскольку на практике это обычно не выполняется, их можно использовать для расчета оценки дисперсии наблюдений.

Обозначим

(3.5)

Эта величина является по существу остаточная дисперсия, которая используется в качестве оценки дисперсии ошибок наблюдений

(3.6)

Уровень значимости обычно выбирают равным и из таблиц t-распределения находят значение . Дисперсия оценок параметров равна

(3.7)

Значимость параметров проверяется обычным способом путем проверки неравенства

(3.8)

Пример.

Пусть имеем 10 варьируемых параметров. Выбираем план эксперимента Плакетта-Бермана для 16 опытов. 5 факторов принимаем как фиктивные с целью установления дисперсии ошибок при определении коэффициентов . Фиктивными переменными принимаем В результате проведения опытов (таблица 3.3). получены некие функции цели.

Выполнить обработку эксперимента и определить значимые факторы.

Коэффициенты вычислены по формуле 3.3 и приведены в таблице 3.4.

Далее по формуле (3.5) определяем остаточную дисперсию.

Вычисляем дисперсию ошибок наблюдений по формуле (3.7).

= 8059/16=503,7

и

По таблицам при определяем критическое значение

. т.е. .

Следующим этапом производим сравнение полученных оценок с числом 50. Все факторы численно равные 50 будут значимыми, меньше 50 – незначимыми и отвергаются как не влияющие на функцию цели.

Таблица 3.3

N

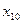
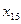
f

+

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

-

+

-

+

+

-

-

+

-

-

-

+

+

+

+

+

-

+

+

-

-

+

-

-

-

+

+

+

+

-

-

+

+

-

-

+

-

-

-

+

+

+

+

-

+

+

+

-

-

+

-

-

-

+

+

+

+

-

+

-

+

-

-

+

-

-

-

+

+

+

+

-

+

-

+

-

-

+

-

-

-

+

+

+

+

-

+

-

+

+

-

+

-

-

-

+

+

+

+

-

+

-

+

+

-

+

-

-

-

+

+

+

+

-

+

-

+

+

-

-

-

-

-

+

+

+

+

-

+

-

+

+

-

-

+

-

-

+

+

+

+

-

+

-

+

+

-

-

+

-

-

+

+

+

+

-

+

-

+

+

-

-

+

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

Таблица 3.4

№		знач.
		да
		нет
		нет
		да
		нет
		нет
		нет
		да
		нет
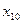
		да
	0.5	нет
		нет
		нет
		нет
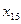
		нет

В таблице:

варьируемые параметры;

коэффициент;

Знач. – значимость

Анализ результатов таблицы показывает, что из всех 10 варьируемых параметров для оказания воздействия на функцию цели значимым оказались только 4:

х1, х4, х8 и х10.

Date: 2015-10-19; view: 2143; Нарушение авторских прав