
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторна робота № 2-6
|
|
Вимірювання електричних опорів і вивчення залежності опору металу від температури
л. 1. §34. 2. §§8.3,8.4,8.5
Мета роботи: навчитись вимірювати опори провідників з допомогою місткових схем; вивчити залежність опору металів від температури.
Прилади та матеріали: набір вимірюваних резисторів; магазин еталонних резисторів; джерело постійного струму; універсальний міст типу МВУ-49; термостат і термометр; з’єднувальні провідники.
Теоретичні відомості
Електричним струмом називається направлений рух електричних зарядів. Цьому рухові перешкоджає електричний опір провідників. Розглянемо класичну електронну теорію металів, яка, не дивлячись на деякі недоліки, якісно на хорошому рівні дає пояснення основних законів електричного струму.
У класичній електронній теорії металів припускається, що рух електронів описується законами класичної механіки Ньютона. Електрони створюють ідеальний (електронний) газ, що знаходиться в хаотичному тепловому русі і характеризується середньою довжиною вільного пробігу l і середнім часом вільного пробігу t. Електрони обмінюються енергією і імпульсом з іонами кристалічної гратки, дякуючи чому електронний газ знаходиться в термодинамічній рівновазі з граткою.
Визначимо густину струму j, яка виникає в металі під дією електричного поля з напруженістю E. Електрони, здійснюючи тепловий хаотичний рух, в той же час під дією електричного поля рухаються проти нього. Направлений рух електронів в електричному полі називається дрейфом. Електричне поле прискорює електрони і величина цього прискорення у відповідності з другим законом Ньютона буде пропорційною діючій силі: 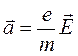 тому в кінці вільного пробігу його швидкість буде дорівнювати
тому в кінці вільного пробігу його швидкість буде дорівнювати


Так як електрони між ударами рухаються рівноприскорено, то середнє значення дрейфової швидкості становитиме половину максимальної:

Якщо концентрація електронів дорівнює n, то за одиницю часу через одиничний переріз пройде заряд, який буде знаходитись в об’ємі паралелепіпеда з одиничним перерізом і довжиною 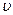 др:
др:

Густина струму пропорційна напруженості поля E, а це і є закон Ома в диференційній формі:
 (1)
(1)
де d – питома електропровідність середовища;  .
.
(r – питомий опір середовища).
Для визначення питомого опору використаєм формулу 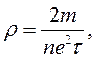 яка показує, що питомий опір тим менший, чим більша концентрація електронів провідності і чим більший час вільного пробігу t.
яка показує, що питомий опір тим менший, чим більша концентрація електронів провідності і чим більший час вільного пробігу t.
Це пояснюється тим, що чим більше t, тим меншу перешкоду мають процеси розсіювання для напрямленого руху електронів.
Питомий електричний опір чисельно дорівнює опору R, виготовленого із даної речовини прямолінійного провідника з постійною по довжині пло-щею перерізу S, рівною одиниці, і довжиною l, рівною одиниці: 
Розмірність R визначається за законом Ома:


Одиниця питомого опору речовини:
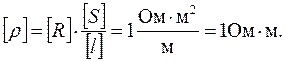
Для більшості металів при температурах, близьких до
Рис. 1
кімнатної, питомий опір змінюється пропорційно абсолютній температурі Т:
 . (2)
. (2)
При низьких температурах спостерігається відхід від цієї закономірності (рис, 1), пояснення якої дається квантовою механікою.
У більшості випадків залежність r від T дається графіком 1. Величина залишкового опору r ЗАЛ в великій мірі залежить від чистоти матеріалу і залишкових механічних напружень в зразку. Тому після відпалювання r ЗАЛ значно зменшується. У абсолютно чистого металу з ідеально правильною кристалічною граткою при абсолютному нулі r=0.
Із формули (2) слідує, що температурний коефіцієнт опору:
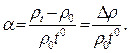 (3)
(3)
Він вказує на відносний приріст питомого опору при збільшенні температури на один градус.
Вимірювання опору резисторів має широке практичне значення. У залежності від призначення резисторів електричні опори у них можна розділити на три групи: малі -до 1 Ом (опори амперметрів, шунтів, обмоток трансформаторів і т.п.), середні 1- 100 кОм (опори вольтметрів і т.п.), великі - 100 кОм і більше (опори ізоляційних матеріалів, кераміка і т.п.).
Методи вимірювання електричних опорів залежать від їх величин. При вимірюванні малих опорів слід ліквідувати вплив на результати вимірювань з’єднувальних провідників, контактів і термо ЕРС, тоді, як при вимірюванні середніх опорів, величинами додаткових опорів (як правило не перевищують 10-4-10-2 0м) можна знехтувати. При вимірюванні великих опорів необхідно враховувати об’ємні і поверхневі опори, вплив температур і вологості середовища.
Скориставшись законом Ома для ділянки кола, можна виміряти невідомий опір Rх за допомогою вольтметра і амперметра згідно схеми на рис. 2 і 3.

Цей метод покладений з основу дії авометрів, за допомогою яких можна виміряти напругу, силу струму, опір. Але так як при такому методі вимірювання відбувається спад напруги на вольтметрі і амперметрі, то метод вважається наближеним.
Вимірювання середніх опорів Rх з високим ступенем точності можна виконати мостовим методом за допомогою містка Уітстона.
Існує лише єдине співвідношення параметрів, при якому струм через гальванометр дорівнює нулю:
 (4)
(4)
де R1 – плече порівнювання;
R2 і R3 – плечі відношення.
Як видно із формули (4), можливими є два методи зрівноважування містка: а) регулюванням R1 при постійному відношенні R2/R3; б) регулю-ванням відношення R2 / R3 при постійному R1.
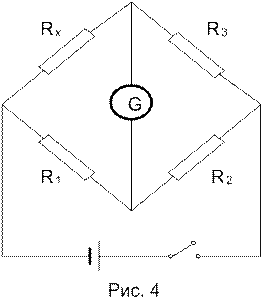
В першому випадку R1 виконується в вигляді багатодекадного важільного магазину опорів; R2 і R3 являють собою набір опорів з клемами для підключення. У другому випадку відношення плеч виконане у вигляді реохорда з повзунком (рис. 5).
Умові рівноваги такого містка відповідає співвідношення:

яке може бути одержане на основі другого закону Кірхгофа.
Так як опори ділянок АD і DВ. пропорційні їх довжинам l1 i l 2, то
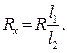

Недоліком місткової схеми є неможливість врахувати опори з’єднувальних провідни-ків і клемних сполучень елементів схеми, що виключає можливість вимірювання малих опорів
Для технічного вимірювання опорів можна скористатись універсальними містками постійного струму типу МВУ-49, схема якого в принципі не відрізняється від схеми лінійного містка Уітстона (рис. 6).
В цій схемі плечем порівнювання служить магазин опорів, набраний із резисторів R1¸Rn. Відношення плеч визначається за формулою


Вимірюваний і опір резистора Rх визначається на основі рівноваги моста:

де N –множник, який відповідає положенню рукоятки перемикача “помножити”;
R – опір плеча порівняння в Ом (показання магазина).
Опір R3 є захисним при включенні гальванометра в схему і відповідає положенню кнопки включення “Грубо”.
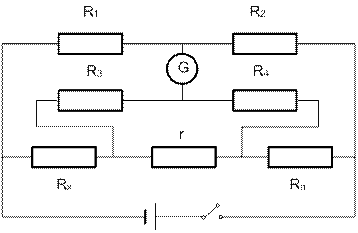
Із всіх методів вимірювання малих опорів найбільше по-ширення одержав метод вимірю-вання за схемою подвійного моста, запропонованого Томсоном (рис.7). У такій схемі вплив з’єднувальних провідників і клем практично виключається.
У даній лабораторній роботі подається місткова схема вимірювання невідомих опорів.
|
1. Скласти схему (рис. 5).
2. Установити повзунок на середину реохорда.
3. Підібрати на магазині опорів такий опір, при якому струм через гальванометр дорівнював би нулю (Rх1»R).
4. Виміряти l 1 і l 2 - плечі реохорда в одиницях шкали реохорда.
5. Повторити аналогічні вимірювання послідовно для всіх резисторів Ri.
6. З’єднати резистори паралельно і виміряти їх загальний опір. Зробити перевірку вимірювання за допомогою аналітичних розрахунків.
7. З’єднати всі резистори послідовно і виміряти їх загальний опір. Зробити перевірку вимірювання за допомогою аналітичних розрахунків.
8.
|
9. З’єднати провідниками резистор із мідного дроту, розміщений в термостаті з мостом постійного струму типу МВУ.
10. Виміряти опір досліджуваної котушки при кімнатній температурі.
11. Включити нагрівник термостата і провести вимірювання опору котушки через 5°С до температури 80-90°С.
12. Скласти таблицю 2 і занести в неї всі одержані результати.
Обробка одержаних експериментальних результатів і їх аналіз.
1. Використовуючи дані таблиці 2, побудувати графік залежності Rt=f (t°), відкладаючи по осі X значення температури від 0°С до t° С, а по осі Y значення Rt.
2. Із графіка визначити значення R0 шляхом продовження одержаної залежності до перетину з віссю Rt (рис.8).

Рис.8.
3. Розрахувати значення a, за формулою (З), скориставшись даними графіка. Одержаний результат порівняти з табличним значенням температурного коефіцієнту опору для міді.
Додаткові завдання
1. Дослідити вплив швидкості нагріву (охолодження) на точність побудованої залежності Rt=f (t°).
2. Дослідити величину температурного коефіцієнта опору в різних межах зміни температури і виявити залежність a=f (t°),.
Лабораторна робота № 2-7
Вивчення законів постійного струму
л.1.§§34,35. 2.§§ 9.2,9.3
Мета роботи: перевірка закону Ома для неоднорідної ділянки кола.
Прилади і обладнання: джерело струму на б В, два джерела на 1,5В; вольтметр; амперметр; реостати.
Теоретичні відомості
Електричний струм - упорядкований рух електричних зарядів. У металах - це рух електронів проти поля, в електролітах – іонів різних знаків у протилежних напрямках, у газах – електронів та іонів, у напівпровідниках - електронів і дірок. Для збудження електричного струму в тілах треба створити електричне поле. Щоб струм був тривалим, енергія поля повинна підтримуватись сталою. Це здійснюється за допомогою джерела струму.
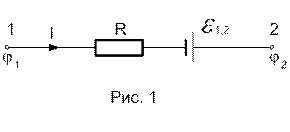
Закон Ома у формі U=IR справджується лише для однорідної ділянки кола, тобто такої, на якій немає стрибків потенціалів за рахунок контактних явищ або дії електрорушійних сил.
Розглянемо неоднорідну ділянку кола 1-2 (рис. І), на кінцях якої діє різниця потенціалів j1-j2. Е.р.с., що діє на даній неоднорідній ділянці кола, позначимо через e1,2.
Знайдемо напрям струму (j1>j2). Тоді e1,2>0, якщо вона діє в напрямі струму (позначено стрілкою). Скористаємось законом збереження і перетворення енергії. Оскільки провідники нерухомі, то робота dA електростатичних і сторонніх сил, яка виконується при переміщенні заряду dq на ділянці 1-2, дорівнює кількості тепла dQ, яке виділилось під час проходження заряду dq.
Тому можна записати:

Прирівнявши праві частини цих рівнянь, будемо мати:
 (1)
(1)
Це - закон Ома для неоднорідної ділянки кола.
Якщо неоднорідна частина кола складається з кількох ділянок, то формулу (1) можна узагальнити на будь-яке число ділянок:
 (2)
(2)

де  — загальний опір усієї ділянки кола;
— загальний опір усієї ділянки кола;
 — алгебраїчна сума е.р.с., що діють на цій ділянці.
— алгебраїчна сума е.р.с., що діють на цій ділянці.
Хід роботи
1. Скласти електричне коло за схемою, показаною на рис.2.
2. Замкнути вимикач 1, потім 2. Резисторами R1 і R2 добитися значення сили струму 0,3 А.
3. Виміряти значення I, UAB, R1, R2, R3. Результати вимірювань занести до таблиці, яку слід нарисувати самостійно.
4. Обчислити величини, які входять до лівої і правої частини рівняння (2):

При цьому слід врахувати знаки e1 і e2.
5. Зміною опорів R1 ,R2 ,R3 підібрати в колі струми 0,З5 А; 0,40 А; 0,45А та провести необхідні обчислення згідно пунктів З, 4.
6. Обчислити похибки вимірювань за класом точності вимірювальних приладів та перевірити рівність (2). Зробити відповідні висновки.
Контрольні запитання
1. За яких умов при перевірці закону Ома для неоднорідної ділянки кола можна знехтувати внутрішнім опором амперметра?
2. Чому можна нехтувати внутрішніми опорами джерел струму?
3. Вказати межі застосування закону Ома.
Лабораторна робота № 2-8
Вивчення законів Кірхгофа для розгалужених електричних кіл
л.1. §36.2. §9.4
Мета роботи: набути навиків складання електричних кіл і вимірювання струмів і напруг.
Прилади і обладнання: джерела струму;амперметр; вольтметр;набір резисторів; провідники.
Теоретичні відомості
Розглянемо розгалужене електричне коло, в окремі ділянки якого включені джерела струму з відомими е.р.с. Розрахунок такого кола можна провести користуючись законом Ома для неоднорідної ділянки кола і законом збереження заряду. Однак завдання значно спрощується, якщо скористатися двома законами Кірхгофа або правилами Кірхгофа, які є дальшим узагальненням закону Ома для неоднорідної ділянки кола.
Перший закон Кірхгофа формулюється так: алгебраїчна сума струмів, які сходяться у вузловій точці, дорівнює нулю:
 (1)
(1)
Струми які входять до вузлової точки, вважаються додатними, а струми, які виходять з неї, — від’ємними. Наприклад, для вузлової точки С (рис. 1) на основі (1) можна записати:
 (2)
(2)
Перший закон Кірхгофа виражає закон збереження електричного заряду. Рівняння (1) можна записати для кожного із n вузлів складного кола, але незалежними будуть n-1 рівняння.
Другий закон Кірхгофа можна сформулювати так: у будь-якому замкненому контурі розгалуженого електричного кола алгебраїчна сума спадів напруг (тобто добутків сил струмів в окремих ділянках контура на їх опір) дорівнює алгебраїчній сумі електрорушійних сил, що діють в даному контурі.
 (3)
(3)
Фізичний зміст цього результату полягає в тому, що робота з переміщення заряду вздовж будь-якого замкненого контура дорівнює тільки роботі сторонніх сил, а робота сил електростатичного поля вздовж замкненого контура дорівнює нулю.
При складанні рівнянь за другим законом Кірхгофа вибирають незалежно замкнені контури, які можна виділити в даному розгалуженому колі. Оскільки ліва і права частини рівняння (3) являють собою алгебраїчні суми, то умовилися вважати знак добутку IiRi додатним, коли струм Ii збігається з наперед вибраним напрямком обходу контура і від’ємним, коли напрям струму протилежний напрямові обходу. Знак е.р.с. додатний, коли напрям власного струму збігається з напрямом обходу контура.
Розглянемо, наприклад, складне коло на рис. 1.

Рис.1
Застосовуючи правила Кірхгофа, можна дотримуватись такої схеми:
1. Визначити довільно напрями струмів, які входять і виходять з вузлових точок та проходять в окремих ділянках замкненого контура.
2. Вибрати довільно напрям обходу контура і, користуючись рекомендованим вище правилом встановлення знаків доданків алгебраїчних сум, скласти шукані рівняння.
3. Складеними рівняннями охопити всі е.р. с, і всі опори даного замкненого контура.
Застосуємо перше правило Кірхгофа до вузла D:
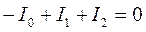
Вибираємо напрям обходу за годинниковою стрілкою,
тоді для контура АВМКА: I1 R1 + I0 R3 = - e1
для контура АВDСА: I1 R1 - I2 R2 = e2 - e1,
Ці два рівняння взаємно незалежні. Для контура СDМКС рівняння вже не є незалежним, воно-результат накладання двох попередніх контурів один на другий. Маємо три рівняння з трьома невідомими, і, розв’язавши систему, визначимо невідомі струми.
Порядок виконання роботи
1. Скласти електричне коло за однією із поданих схем для бригад: 1,5,9 — рис. 2; 2, 6, 10 — рис. 3; 3, 7, II — рис 4; 4, 8,12 — рис. 5.
2. Після перевірки змонтованої схеми лаборантом або керівником занять включити в коло живлення.
3. Підключаючи паралельно кожній ділянці кола вольтметр, виміряти спад напруги на всіх ділянках кола.
4. Виміряти ЕРС джерел струму, для чого підключити вольтметр паралельно джерелу при розімкненому колі.
5. Виміряти струм на всіх ділянках кола, для чого через гнізда підключити у відповідні вітки амперметр.
6. Виміряні результати занести в таблиці 1, 2, 3.
Табл. 1
| № | e1 | e2 | U1 | U2 | I1 | I2 | r0,1 | r0,2 |
Табл. 2
| I1 | I2 | I3 | I4 | I5 | I6 |
Табл. 3
| U1 | U2 | U3 | U4 | U5 | U6 | R1 | R2 | R3 | R4 | R5 | R6 |
Обробка результатів вимірювань
1. Користуючись законом Ома і одержаними при вимірюванні результатами, розрахувати недостаючі параметри для складання правил Кірхгофа.
2. Результати розрахунків занести в таблиці 1,2,3,
3. Користуючись даними таблиць 1,2,3 скласти рівняння першого і другого правил Кірхгофа.
4. У випадку невиконання законів Кірхгофа провести повторні вимірювання більш уважно, враховуючи похибки електровимірювальних приладів.
Контрольні питання
1. Виведіть закон Ома в диференціальній формі на основі електронних уявлень.
2. Як практично використовують правила Кірхгофа для розгалужених кіл?
3. Який порядок розрахунків параметрів розгалужених кіл постійного струму.
Лабораторна робота № 2 - 9
Зміна чутливості електровимірювальних приладів
л. 2. §17.2.
Мета роботи: освоїти методику розширення меж вимірювання електровимірювальних приладів.
Прилади і матеріали: мікроамперметр на 100-300мкА; міст постійного стру-му; еталонний амперметр класу точності не нижче 0,5; еталонний вольтметр такого ж класу точності; джере-ло е.р.с. до 10-12В; мідна або константанова дротина для шунтів; реостати до 30 Ом на струми не менше 3А; магазин опорів.
Теоретичні відомості
Розглянемо способи розширення меж вимірювання або зменшення чутливості вимірювальних приладів — амперметрів та вольтметрів постійного струму.
Основною частиною будь-якого амперметра і вольтметра постійного струму є високочутливий прилад магнітоелектричної системи (мікроамперметр або міліамперметр). Незалежно від того, в якій схемі використовується мікроамперметр — при вимірюванні великих струмів, великих напруг або опорів провідників, він має певну чутливість і стрілка його відхиляється на всю шкалу при проходженні через нього певного струму I0. У зв’язку з цим, коли потрібно вимірювати великі струми з номінальним значенням Iн = nI0, де n може бути числом порядку 10¸105, до мікроамперметра паралельно підключають шунт ri ( рис. 1,а).
Величину опору шунта визначають із співвідношення
 (1)
(1)
де r0 – внутрішній опір мікроамперметра;
n – число, яке показує, в скільки разів зменшується чутливість приладу.
Для вимірювання великих напруг з номінальним значенням Un до мікроамперметра послідовно підключають додатковий опір (рис.1,б), величина якого визначається формулою:
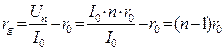 (2)
(2)

Амперметр і вольтметр постійного струму мають ряд переваг: вони можуть бути приладами високого класу точності, майже не чутливі до сторонніх магнітних полів, а шкали їх рівномірні. Виготовлені амперметри чи вольтметри градуюють за еталонними приладами.
Схему для градуювання амперметра подано на рис.2.
Обидва амперметри — еталонний Ае і досліджуваний А — вмикаються послідовно. Реостатом R1 добирають певні струми, які відхиляють стрілку досліджуваного амперметра до відповідних поділок його шкали.
Величини цих підібраних струмів визначають за еталонним ампер-метром Ае. Аналогічно градуюють вольтметр за схемою, поданою на рис.3.

Після потенціометра R1 напруга подається на вольтметр Ve i V. Для точного встановлення напруги заданої величини, користуються додатковим реостатом R2. При градуюванні знаходять ряд значень I(j) і U(j) для досліджуваних амперметра і вольтметра, на основі яких будують робочі графіки.

Порядок виконання роботи
1. Підібравши відповідний мікроамперметр з номінальним значенням струму I0 і внутрішнім опором r0, розрахувати за формулою (І) шунт для заданого n. Величину n визначає викладач безпосередньо на занятті.
2. За допомогою моста підібрати шунт потрібного опору так, щоб густина струму в ньому становила 4 А/мм2. Довжина шунта має бути такою, щоб був деякий запас, потрібний для закріплення шунта в клемах.
3. Під’єднати шунт до клем мікроамперметра i за схемою, поданою на рис.2, проградуювати прилади в одиницях струму за еталонним амперметром.
4. Обчислити за формулою (2) додатковий опір для заданої номінальної напруги UU. Підібрати потрібний опір ry за допомогою магазину опорів.
5. Під’єднавши опір ry до мікроамперметра за схемою, поданою на рис.3, проградуювати його в одиницях напруги за еталонним вольтметром.
6. Побудувати на міліметровому папері робочі графіки I(j) і U(j). Перевірити, чи зберігається на графіках лінійність цих функцій.
Контрольні запитання.
1. Що називається чутливістю вимірювального приладу?
2. Як визначити клас точності вимірювального приладу?
3. Абсолютна і відносна похибки вимірювальних приладів.
Лабораторна робота № 2-10
Експериментальне визначення термо-е.р.c. термопари
Мета роботи: набути навиків експериментального визначення коефіцієнта термо-e.p.c. термопари.
Прилади і матеріали: хромель-алюмелева термопара; два термометри; електрична пічка; потенціометр ПП-63.
Теоретичні відомості
Коло явищ, пов’язаних з виникненням термоелектричного струму при різній температурі контактів, а також явищ Пельтьє і Томсона, дістали назву термоелектричних явищ.
Розглянемо замкнене коло, складене з двох різнорідних металів А і В (рис.1). Місця спаїв 1 і 2 будемо підтримувати при однаковій температурі. В місцях контактів 1 і 2 виникнуть контактні різниці потенціалів j1 - j2, але в колі струму не буде:
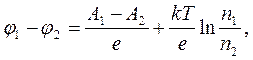 (1)
(1)
де А1 і А2 – роботи виходу електронів із металів;
k – стала Больцмана;
Т – абсолютна температура;
n1 і n2 – концентрації вільних електронів в металах;
e — заряд електрона.
Це пояснюється тим, що у тонкому шарі контакту двох металів виникає подвійний електричний шар і його поле гальмує дальший перехід електронів — настає динамічна рівновага.
При нагріванні спаїв 1 і 2 до різних температур Т1 і Т2, у колі виникає струм, а термо-е.р.с. буде дорівнювати різниці контактних різниць потенціалів j1-j2:
 (2)
(2)
де 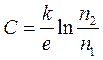 — стала термопари, яка дорівнює е.р.с., що виникає при різниці температур спаїв в 1°С. Таким чином, з формули (2) видно, що е.р.с. термопари пропорційна різниці температур її спаїв.
— стала термопари, яка дорівнює е.р.с., що виникає при різниці температур спаїв в 1°С. Таким чином, з формули (2) видно, що е.р.с. термопари пропорційна різниці температур її спаїв.
Експеримент показує, що стала термопари С у різних пар металів і даної пари металів для різних температурних інтервалів має різне значення. Отже, треба визначити диференціальні значення сталої термопари для окремих температурних інтервалів:
 (3)
(3)
Термопарою називають пристрій з двох різнорідних провідників, з’єднаних між собою надійним контактом (зварені або спаяні) (рис.1).
Явище виникнення е.р.с. в термопарі (2), спаї якої знаходяться при різних температурах, називається ефектом Зеєбека.
При включенні в термопарне коло джерела сторонньої е.р.с. і виникненні при цьому у колі струму, спаї термопари будуть охолоджуватись або нагріватись. Це явище носить назву явища Пельтьє. При цьому теплова енергія або поглинається, або виділяється.
± DQ = П I t, (4)
де П –коефіцієнт Пельтьє;
t – час;
I – величина струму.
Термопари широко застосовуються для вимірювання і контролю за сталістю температури — це так звані термоелектричні термометри, які складаються з термопари і приладу, що вимірює термо-е.р.с..
Явище Пельтьє реалізується в численних пристроях і термостатах, в яких охолодження або стабілізація температури може здійснюватись аж до -130°С.
Перевагою всіх термоелектричних пристроїв, як металевих так і напівпровідникових є їх простота, висока надійність, повна автономність, безшумність, мініатюризація і т.п. Недоліком таких пристроїв є низький к.к.д., який не перевищує 10-12%.
Для збільшення величини термо-е.р.с. термоелементи збирають в батареї (рис.2)
Парні спаї такої термобатареї підтримують при одній температурі, а непарні — при іншій.
Залежно від інтервалу робочих температур на практиці застосовують такі типи термопар:
1. До 1900 К — група ПП, платина- платинородій, С= 6,4×10-3 мВ/К.
2. До 1300 К— група ХА, хромель- алюмель, С= 4, 2×10-2 мВ/К.
3. До 900 К— група ХК, хромель-копель, С= 6,95×10-2 мВ/К.
4. До 600 К— група МК, мідь-копель, С= 4,75×10-2 мВ/К.
5. До 500 К— група МК, мідь-константан, С=4×10-2мВ/К.
У даній лабораторній роботі визначається термоелектрична стала С хромель-алюмелевої термопари. Лабораторна установка складається згідно рис.3.

На рис.3: А— термостат — посудина, заповнена рідиною при кімнатній температурі; В — нагрівальна пічка; D — потенціометр постійного струму ПП63; К-термометри; М-термопара.
Порядок виконання роботи
1. Перед початком виконання лабораторної роботи лаборант приводить потенціометр ПП-63 до робочого стану. При цьому виставляється робочий струм і така напруга, що при однаковій температурі спаїв гальванометр, в колі потенціометра, повинен знаходитись на відмітці “нуль”.
2. Включити електричну пічку і через кожні 5°С виміряти величину термо-е.р.с. в мВ. Вимірювання продовжувати до 80-90°С.
3. Результати вимірювань термо- е.р.с. і температури занести в таблицю.
4. На міліметровому папері побудувати графік залежності e=f (T).
5. Користуючись одержаним графіком, визначити коефіцієнт термо-е.р.с. С, який у цьому випадку чисельно буде рівний тангенсу кута нахилу одержаної прямої до вісі температур.
6. Оцінити похибки вимірювань.
Контрольні запитання
1. У чому полягає суть термоелектричних явищ? Яка їх природа?
2. Охарактеризуйте області застосування термопар?
Лабораторна робота №2-11
Вивчення явища термоелектронної емісії
л. 2. §§10.3,10.4
Мета роботи: вивчити явище термоелектронної емісії і його використання в електронних лампах.
Прилади та матеріали: змонтований макет лабораторної установки.
Теоретичні відомості
У сучасній техніці широко використовуються електровакуумні прилади —радіолампи, електронно-променеві трубки, фотоелектронні помножувачі, вакуумні фотоелементи тощо. Дія цих приладів заснована на проходженні струму у вакуумі. При цьому мова йдеться про технічний вакуум (розрідження становить 10-6 -10-7 Па).
Розглянемо процеси, які відбуваються в електронній лампі при постійному струмі розжарення катода.
У відсутності анодної напруги навколо розжареного катода утворюється так звана електронна хмара, яка являє собою просторовий негативний заряд. У стані термодинамічної рівноваги число електронів, які вилетіли з катода, дорівнює числу електронів, що повернулись в метал. При цьому густина електронної хмари тим більша, чим вища температура катода.
Між катодом і анодом створюється електричне поле, під дією якого і відбувається напрямлений рух електронів, тобто електричний струм у вакуумі. Залежність струму через діод від прикладеної напруги має досить складний характер. При деякому значенні Ua=Uн всі електрони досягають анода, а струм стає таким, що дорівнює струмові насичення, і дальше його зростання припиняється (рис.1).
Така залежність струму від напруги називається анодною (вольт-амперною) характеристикою діода. При невеликих значеннях напруги струм зростає пропорційно Ua3/2. Цю залежність встановили С.Богуслав-ський та І.Ленгмюр, і називається вона законом трьох других. Формула Богуславського-Ленгмюра має вигляд:
 (1)
(1)
де k – коефіцієнт пропорційності, який залежить від форми і розмірів електродів лампи.
Формула (1) справедлива при досить великих емісіях катода. Тому, для досягнення якомога більшої термоелектронної емісії, матеріал повинен мати найменшу роботу виходу.
Емісійну здатність матеріалу катода визначає густина термоелектрон-ного струму насичення, що характеризує максимальну кількість електронів, які можуть покинути метал з одиниці поверхні за одиницю часу.
Для визначення густини термоелектронного струму насичення користуються моделлю, згідно з якою сукупність вільних електронів в металі вважають як ідеальний електронний газ, до якого застосовна квантова статистика Фермі-Дірака. Розрахунки, виконані на основі квантової статистики, приводять до такої формули:
 (2)
(2)

рис. 1
де ej — робота виходу;
A — стала, яка не залежить від роду матеріалу (теоретичне значення її 1,2×106 А/м К).
Вперше аналітичну залежність струму насичення від роботи виходу встановив О.Річардсон на основі термодинамічних міркувань. Пізніше Дешман вивів цю формулу на основі квантово-механічних міркувань. Тому формула (2) дістала назву формули Річардсона-Дешмана. Ця формула досить добре узгоджується з експериментом. Як видно з (2) густина термоелектронного струму насичення досить швидко зростає з підвищенням температури катода і визначається також значенням роботи виходу. Тому, щоб дістати великий струм насичення, а також для збільшення строку роботи лампи потрібно знижувати робочу температуру катода. Це досягається застосуванням так званих складних катодів: барієвих, цезієвих, оксидних та інших, зяких найефективнішим є оксидний. Оксидний катод складається із нікелевого або вольфрамового провідника, на який нанесено суміш оксидів барію і стронцію. Це дає змогу, згідно з формулою (2), одержати великі густини струму при порівняно невисоких температурах (1000-1170 К). Оксидні катоди знайшли широке застосування в електровакуумних приладах.
Технічне значення електронних ламп визначається тим, що електронним струмом в лампі можна легко керувати. Для цього в електронні лампи вводять ще один або кілька додаткових металевих електродів; їх часто виготовляють у вигляді проволочних спіралей і розміщують між катодом і анодом. Ці додаткові електроди одержали назву сіток. На рис.2 показано схематичне зображення тріода.

Оскільки сітка розміщена ближче до катода і певною мірою “екранує” вплив анода на катод, то незначна зміна потенціалу на ній досить сильно впливає на величину анодного струму.
Отже, якщо на сітку подати навіть невеликий позитивний потенціал, електрони прискорюються і, навпаки, навіть незначний негативний потенціал гальмуватиме електрони.
Рис.2
Графіки, які визначають залежність анодного струму Ia від анодної напруги

Рис. 3
на сітці Uc при сталій анодній напрузі (Uа = const), називаються сітковими характеристиками лампи (рис. 3).
Для різних анодних напруг запірний потенціал Uз різний (рис. 3). Для більших анодних напруг запірний потенціал більший. Тому для різних значень напруг можна дістати так зване сімейство сіткових характеристик, з яких визначають основні параметри тріода; крутизну сіткової характеристики S, внутрішній опір R і коефіцієнт підсилення m.
Для визначення параметрів лампи методом трьох точок треба на прямолінійній ділянці двох сіткових характеристик побудувати характеристичний трикутник АВС (рис. 3). Сторона АВ визначає зміну напруги на сітці лампи DUc, ВС — зміну анодного струму Ia. Визначивши величину DUа = Uа2- Uа1, можна обчислити параметри лампи.
Крутизна сіткової характеристики є показником ступеня підсилення лампи і визначається як тангенс кута нахилу характеристики
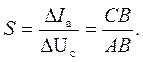 (3)
(3)
Внутрішній опір - відношення приросту анодної напруги до викликаного нею приросту анодного струму (при сталій напрузі на сітці лампи).
 (4)
(4)
Коефіцієнт підсилення m дорівнює відношенню зміни анодної напруги DUа до зміни напруги на керуючій сітці DUc, які спричиняють ту саму зміну анодного струму?
 (5)
(5)
Величина, обернена до коефіцієнта підсилення, називається проникністю лампи D:
 (6)
(6)
Розглянуті характеристики належать до так званого статичного режиму роботи лампи, тобто такого, коли в анодному колі немає анодного навантаження. При наявності анодного навантаження параметри лампи і режими її роботи називають динамічними.
На рис. 4 наведено схему для визначення основних параметрів тріода і зняття анодних та сіткових характеристик. K1, K2 – подільники напруги; П – перемикач, яким можна змінювати знак потенціалу на сітці лампи.
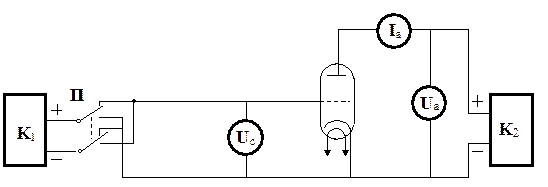
Рис. 4.
Порядок виконання роботи
1. Скласти коло за схемою на рис. 4, дотримуючись полярності подільників напруги K1, і K2.
2. Зняти вольт амперну характеристику Ia = f(Ua) при Uc = 0 та сіткові характеристики Ia = f(Uc) при двох значеннях анодної напруги: Ua = 40 В і Ua = 60 В. При зніманні сіткових характеристик слід підтримувати постійними значення анодної напруги.
3. Подільником напруги K1 добитися відсутності анодного струму. Записати покази вольтметра Uс. Потім, збільшуючи напругу на сітці через 0,5-1 В, записати покази міліамперметра в анодному колі. Дані занести до таблиці.
4. Подати на керуючу сітку невеликий позитивний потенціал (наприклад 2 або 3В). Змінюючи анодну напругу через 5-10В, фіксувати покази міліамперметра в анодному колі. Дані занести до таблиці. Стежити, щоб анодний струм досяг максимуму.
5. Побудувати графіки Ia = f(Uа) та Ia = f(Uc).
6. З графіків сіткових характеристик визначити за формулами (3), (4), (5), (6) параметри лампи.
Контрольні питання
1. Яка будова і принцип дії вакуумного діода та тріода?
2. Які основні параметри тріода?
3. У чому суть явища термоелектронної емісії?
4. Від чого залежить термоелектронний струм насичення?
5. Як формулюється закон трьох других? Поясніть його.
Розділ третій.
Електромагнетизм
До кожної лабораторної роботи подано посилання на слідуючі підручники:
1. Савельев И.В.. Курс общей физики. Т. 2. М: Наука: 1978.
2. Яворский Б.М.. Курс физики. Т.2. М: Наука: 1978.
Лабораторна робота № 3-1
Визначення індукції магнетного поля за допомогою
балістичного гальванометра
л.1. §§ 40, 41, 43. 2. §§15.1, 15.2, 15.3, 14.4
Мета роботи: засвоєння навичок вимірювання індукції магнетного поля і дослідження залежності індукції поля від форми полюсів магнету.
Прилади і матеріали: електромагнет; балістичний гальванометр; вимірювальна котушка; реостат; джерело постійного струму; двохлолюсний перемикач.
Теоретичні відомості
На провідник із струмом в магнетному полі діє сила Ампера:


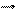

 Вектор B називається магнетною індукцією і є основною характеристикою магнетного поля. Закон Ампера дозволяє визначити числове значення магнетної індукції B. Якшо елемент струму Idl перпендикулярний до B, то формулу (1) можна записати у вигляді:
Вектор B називається магнетною індукцією і є основною характеристикою магнетного поля. Закон Ампера дозволяє визначити числове значення магнетної індукції B. Якшо елемент струму Idl перпендикулярний до B, то формулу (1) можна записати у вигляді:
 (2)
(2)
З формули (2) випливає, що магнетна індукція є силовою характе- ристикою магнетного поля. Одиниця магнетноі індукції – тесла (Тл) – магнетна індукція такого однорідного магнетного поля, яке діє з силою 1Н на кожний метр довжини прямолінійного провідника з струмом 1А, розташованого перпендикулярно до напрямку поля. З (2) маємо:
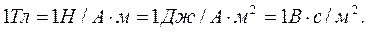 (3)
(3)
 Однією з основних величин електромагнетизму є магнетний потік. Потоком вектора магнетної індукції, або магнетним потоком через малу площину dS, називається фізична величина, що дорівнює добуткові цієї площі на проекцію Вn вектора B на напрямок нормалі n до неї. Це є скалярним добутком векторів B i dS (рис. 1)
Однією з основних величин електромагнетизму є магнетний потік. Потоком вектора магнетної індукції, або магнетним потоком через малу площину dS, називається фізична величина, що дорівнює добуткові цієї площі на проекцію Вn вектора B на напрямок нормалі n до неї. Це є скалярним добутком векторів B i dS (рис. 1)
 (4)
(4)
Магнетний потік через довільну поверхню S можна знайти шляхом інтегрування виразу елементарного потоку dF по всій поверхні S, тобто
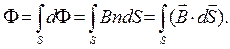 (5)
(5)
Розглянемо електричне коло, що складається з гальванометра G івимірювальної котушки ВК, розташованої в магнетному полі електромагнету між його полюсами (рис.2).

Рис.1
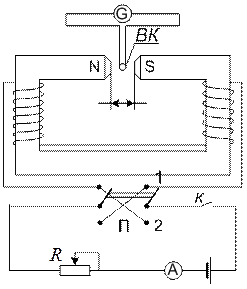
Рис.2
Наявність повітряного проміжку приводить до зменшення B, причому, із збільшенням розмірів повітряного проміжку l0 магнетна індукція зменшується.
Якщо магнетна індукція в місці знаходження вимірювальної котушки стала ( ), то струм в колі гальванометра відсутній. Якщо ж перемикач П перемкнути з положення 1 в положення 2 (чи навпаки),
), то струм в колі гальванометра відсутній. Якщо ж перемикач П перемкнути з положення 1 в положення 2 (чи навпаки),
магнетна індукція поля за певний час зміниться від B до -B. Так як гальванометр G балістичний, він покаже кількість електрики q, яка протекла в колі протягом часу t. Знаючи q, можна визначити B (див. теорію методу лабораторної роботи № 3-4).
Відомо, що:
 (6)
(6)
Враховуючи, що для повітря m=1 та підставляючи в (6) значення Н з (10) (лаб. робота №3-4), одержимо робочу формулу:
 (7)
(7)
Порядок виконання роботи
Завдання 1.
1. Зібрати схему згідно з рис.2.
2. Виставити ВК (вимірювальна котушка) в центрі повітряного проміжку.
3. Довжину l0 зробити рівною 20 мм.
4. За допомогою реостата R підібрати такий струм, щоб при перемиканні П покази гальванометра були максимальними. Записати показ n гальванометра і координату х котушки.
5. Зняти 8 - 10 показів n та х, кожний раз переміщуючи вимірювальну котушку на 1 см вправо (чи вліво).
6. Встановити l0=30 мм. Повторити вимірювання п.п. 4-5, переміщуючи котушку до центру повітряного проміжку.
Завдання 2.
1. Встановити l0=20 мм. При виконанні цього завдання котушка весь час залишається в центрі повітряного проміжку.
2. Записати покази амперметра. Перемикачем П змінити напрям струму в намагнічуючій котушці і при цьому записати покази n гальванометра.
3. За допомогою реостата R змінити величину струму на 0,05-0,1 А. Записати одержане значення струму. Перемикач перемкнути з положення 1 в2 і записати відповідний показ гальванометра.
4. Зменшувати струм до нуля з вибраним кроком. Кожний раз перемикачем П міняти напрям струму, записувати його значення та відповідні їм покази гальванометра.
Обробка результатів експерименту та їх аналіз
Завдання1.
1. За формулою (7) розрахувати магнетну індукцію В для всіх експериментальних значень n. Значення R, N, S, та Rq даються на відповідних елементах схеми.
2. В одній системі координат побудувати графіки B=¦(х) для l0=20 мм і l0=30 мм (за вісь х береться пряма, що проходить через центр вимірювальної котушки і паралельна осі гвинта).
Завдання 2.
1. Розрахувати за формулою (7) магнетну індукцію для відповідних значень струму.
2. Побудувати графік залежності B=¦(I). Пояснити результати, одержані в обох завданнях.
Конторольні запитання.
1. Закон Ампера. Природа сил електромагнетної взаємодії.
2. Вектор магнетної індукції, його фізичний зміст та одиниці вимірювання.
3. Що називається магнетним потоком?
4. Робота переміщення провідника з струмом в магнетному полі.
Лабораторна робота № 3-2
Визначення горизонтальної складової напруженості магнетного поля Землі.
л. 1. §§40,41,42. 2. §§ 15.4,15.5,15.6
Мета роботи: визначення горизонтальної складової напруженості магнетного поля Землі.
Прилади та матеріали: тангенс-гальванометр; міліамперметр; реостат; джерело постійного струму; двохполюсний перемикач.
Теоретичні відомості
Земля являє собою природний магнет, полюси якого лежать поблизу географічних полюсів: недалеко від північного географічного полюса розташований південний магнетний полюс S, а поблизу південного географічного - північний магнетний полюс N (рис.1).

Рис. 1
У першому наближенні магнетне поле Землі, подібне полю диполя, поміщеного в центрі Землі, або однорідно намагнеченої кулі, магнетний момент якої дорівнює ~8,3×1022 А×м2 і направлений під кутом ~11,50 до осі обертання Землі.
Характеристикою магнетного поля Землі служить напруженість Н магнетного поля та її складові. Для розкладу вектора Н на складові звичайно вибирають прямокутну систему координат, в якій одну із осей (х) орієнтують в напрямку географічного меридіану, а іншу (y) — в напрямі паралелі.
При цьому додатним вважається напрямок осі х на північ, а осі y – на схід. Третя вісь z в такому випадку прийме вертикальне положення і буде направлена зверху вниз (рис.2). Таким чином значення та напрямок напруженості Н магнетного поля в будь-якій точці можна задати трьома складовими: Нy, Hx, Hz (північною, східною та вертикальною) або трьома елементами земного магнетизму:
· горизонтальною складовою H0 (проекцією вектора  на горизонтальну площину xoy);
на горизонтальну площину xoy);
· магнетним схиленням a (кутом між горизонтальною складовою H0 та площиною географічного меридіана);
· магнетним нахиленням b (кутом між вектором Н та площиною горизонту xoy)
Магнетне поле Землі складається з постійного (стійкого) поля, створеного магнетизмом самої Земної кулі, і змінного поля (або магнетних варіацій), зумовленого електричними струмами, що течуть над земною поверхнею і в земній корі.
Постійне поле різне в різних точках Землі і схильне до повільних (вікових) змін. Для вивчення просторового розподілу постійного поля на географічні карти наносять значення a, H0, Hz, b, з'єднують лініями точки, в яких їх значення рівні.

На картах видно, що b змінюється від 0 в приекваторіальній області до 900 в магнетних полюсах, а H0 і Hx – відповідно від 33,44 А/м та 0 А/м в приекваторіальних областях до 55,73 А/м на полюсах.
Вивчення магнетного поля Землі в минулі геологічні епохи шляхом дослідження магнетних властивостей гірських порід вказує, що напрямок магнетної осі Землі не завжди був однаковим, і, напевне, кілька разів змінювався на прямо протилежні.
Достовірної теорії постійного магнетного поля Землі поки ще немає. Локальні та регіональні магнетні аномалії викликані нерівномірним розподілом у земній корі порід, багатих феромагнітними мінералами. Проте загальної кількості їх, як показують розрахунки, недостатньо для пояснення магнетизму земної кулі в цілому. Припущення про намагнеченість глибинних шарів Землі та її ядра виявляється неможливим, так як в глибинних шарах Землі температура значно вище точки Кюрі всіх відомих феромагнітних речовин. Гіпотеза про зв’язок магнітного поля Землі з її обертанням не підтверджена ні експериментально, ні теоретично.
Більш вірогідно, що головна частина постійного геомагнітного поля пояснюється вихровими електричними стрілами, що течуть в верхніх шарах земного ядра. По теорії Я.І.Френкеля, ці струми - індукційного, а по теорії В.Ельзасера — термоелектричного походження. Розвивається теорія “самозбуджуючого диполя” (Баллард, Такеуті та ін.), згідно якій електричні струми в ядрі виникають в результаті механічних рухів складаючої ядро рідкої речовини, що має високу електропровідність.
Змінне поле не перевищує, як правило,1% постійного поля. Первинною причиною його є електричні струми, що течуть в верхніх шарах земної атмосфери та за її межами. Магнетні варіації поділяються на правильні періодичні (періодом в одну сонячну добу) і неправильні коливання різної форми і амплітуди — магнетні бурі. Вони досить різноманітні по інтенсивності та вигляду: від невеликих короткочасних коливань елементів земного магнетизму до магнетних бур тривалістю від одного до кількох днів, під час яких ампдітуди коливань магнетних елементів можуть перевищувати 10-2 Е. Магнетні бурі тісно зв’язані з іоносферними бурями, бурями земних струмів та полярними сяйвами. Сильні магнетоіоносферні бурі часто супроводжуються порушенням короткохвильового зв’язку.
Характерною формою малих бур є короткоперіодичні коливання, інколи правильного синусоїдального характеру, інколи- менш регулярні. Іншим типом малих бур є невеликі бурі, викликані спалахами ультрафіолетової радіації під час хромосферних вивержень Сонця, які часто супроводжуються повним поглинанням коротких радіохвиль та припиненням зв'язку на денній стороні Землі.
Теорія методу.
Якщо в данній точці Землі вільно підвішати магнетну стрілку (тобто підвішати за центр маси так, щоб вона могла повертатись і в горизонтальній і в вертикальній площинах), то вона встановиться за напрямком напруженості Н магнітного поля Землі в цій точці, тобто вісь стрілки складе кут b з горизонтальною площиною і кут a - з площиною географічного меридіана.
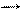 Магнетна стрілка, що може обертатись тільки навколо вертикальної осі, буде відхилятись в горизонтальній площині під дією горизонтальної складової Н0. Слід відмітити, що магнетна стрілка встановлюється в певному напрямі під дією вектора індукції магнетного поля, а не вектора напруженості. Але в силу встановленої традиції будемо говорити про вектор напруженості. Це не внесе значної похибки, так як дослідження проводяться в повітрі і В = m0Н.
Магнетна стрілка, що може обертатись тільки навколо вертикальної осі, буде відхилятись в горизонтальній площині під дією горизонтальної складової Н0. Слід відмітити, що магнетна стрілка встановлюється в певному напрямі під дією вектора індукції магнетного поля, а не вектора напруженості. Але в силу встановленої традиції будемо говорити про вектор напруженості. Це не внесе значної похибки, так як дослідження проводяться в повітрі і В = m0Н.
Розглянемо круговий провідник з N витків, прилягаючих достатньо густо один до одного, розташованих вертикально в площині магнетного меридіану. В центрі провідника помістимо магнетну стрілку, що може обертатись навколо вертикальної осі. Якщо через котушку пропустити струм I, то виникає магнетне поле з напруженістю Hm, направлене перпендикулярно до площини котушки. Таким чином, на стрілку буде діяти два взаємно перпендикулярних магнетних поля: магнетне поле Землі і магнетне поле струму. На рис.3. показано переріз котушки горизонтальною площиною. Тут Нm– вектор напруженості поля, створеного коловим струмом, H0 –горизонтальна складова магнетного поля Землі. Стрілка встановиться за напрямом H1, тобто за напрямком векторної суми Нm і H0.

З рис. 3 слідує:
 (1)
(1)
Напруженість в центрі колового струму знайдемо за законом Біо-Савара -Лапласа:
 (2)
(2)
де N – кількість витків, середній радіус яких рівний R; I – значення сили струму в окремому витку.
З (1) та (2) знаходимо:
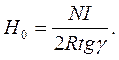 (3)
(3)
Для даного місця Землі і даного приладу величина
 (4)
(4)
є постійною. Тоді
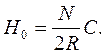 (5)
(5)
З формули (4) слідує, що постійна С чисельно дорівнює струму, який протікає через витки, коли кут відхилення стрілки g = 45°.
Таким чином, коловий провідник з магнетною стрілкою в центрі може бути використаний для вимірювання значення струму. Прилад, оснований на цьому принципі, називається тангенс-гальванометром. Загальний вигляд тангенс-гальванометра показаний на рисунку 4.
Використаний в даній роботі тангенс-гальванометр складається з котушки 1, закріпленої на підставці 3, що обертається. В центрі котушки на вертикальній осі закріплена стрілка 2, під якою є лімб з поділками 4.
Хід роботи.
1. Скласти схему.
Підставку 3 виставити на сферичній поверхні так, щоб кінці магнетної стрілки не торкались лімба 4.
2. Повертаючи тангенс-гальванометр по поверхні 5, встановити його витки в площині магнетного меридіану (магнетна стрілка повинна встановитись на нулі).
3. Ввімкнути котушку на N = 100 витків і, змінюючи струм реостатом R, добитися відхилення стрілки на 45°. Записати значення струму I1¢.
4. Перемикачем П змінити напрямок струму в котушці і знову добитись відхилення стрілки на 45° в протилежний бік. Записати значення струму I2¢.

Рис.4
5. Перевірити нульове встановлення приладу і повторити виміри для N2 =75 i N3 =50 витків. Записати значення струмів I1", I1¢¢¢, I2¢¢, I2¢¢¢.
6. Штангенциркулем виміряти середній діаметр витків котушки.
Додаткове завдання.
1. Перевірити, експериментально, справедливість рівності 
2. Дослідити вплив кута відхилення стрілки g на точність визначення Н0.
Обробка результатів експерименту та їх аналіз
1. Обчислити значення постійних С як середнє значення струмів:

2. За формулою(5) обчислити Н0¢, Н0¢¢, Н0¢¢¢.
3. Розрахувати середнє значення Н0, абсолюту DН0 і відносну E похибки по результатах трьох вимірювань.
4. Обгрунтувати вибраний в даній роботі кут повороту стрілки на 45°, провівши аналіз формули відносної похибки, одержаної з робочої формули, записаної у вигляді:
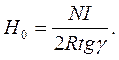
Контрольні запитання.
1. Елементи земного магнетизму.
2. Природа земного магнетизму.
3. Cформулювати закон Біо-Савара-Лапласа.
4. Вивести формулу для напруженості магнетного поля в центрі і на осі колового струму.
5. Пояснити будову і принцип дії тангенс-гальванометра.
6.. Чому виміри проводились при куті відхилення g = 45°?
Лабораторна робота №3-3
Визначення питомого заряду електрона методом магнетного фокусування
л. 1. §§41,43. 2. §§18.1,18.2,18.3,18.4
Мета роботи: визначити питомий заряд електрона з допомогою магнетного фокусування розбіжного електронного пучка.
Прилади та матеріали: електронно-променева трубка з блоком живлення; джерело постійного і змінного струмів; реостат; амперметр; вольтметр.
Теоретичні відомості
Питомий заряд електрона є важливою характеристикою, знання якого необхідне при розрахунках конструкцій різних електровакуумних приладів, електронно-оптичних установок, прискорювачів і т.д. Експериментальні методи визначення e/m засновані на законах руху електронів в електричних і магнетних полях. Ці ж методи використовуються і для визначення маси частинок, якщо відомий їх заряд або заряду при відомій масі.
У даній лабораторній роботі використовується метод фокусування пучка електронів поздовжнім магнетним полем. Принципова схема установки показана на рис. 1.

Рис.1
Електрони, які вилетіли з нагрітого катоду К, прискорюються електричним полем, створеним між катодом і анодом А, входять через малий отвір в аноді розбіжним променем і, попавши на флуоресціюючий екран e створюють світлу пляму.
 Якщо в просторі між анодом і екраном Ee створити магнетне поле з індукцією B, направленою вздовж осі x, то на електрон, який рухається в цьому полі з швидкістю
Якщо в просторі між анодом і екраном Ee створити магнетне поле з індукцією B, направленою вздовж осі x, то на електрон, який рухається в цьому полі з швидкістю  , буде діяти сила Лоренца:
, буде діяти сила Лоренца:
 (1)
(1)
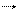 Сила F перпендикулярна як до напряму магнетного поля, так і до напряму руху електрона. Для електрона е < 0, тому сила буде направлена так, як показано на рис. 2.
Сила F перпендикулярна як до напряму магнетного поля, так і до напряму руху електрона. Для електрона е < 0, тому сила буде направлена так, як показано на рис. 2.

Date: 2015-10-19; view: 1726; Нарушение авторских прав