
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Продолжение таблицы 3
|
|
| L | |||||
| Vi | 0,2246 | -0,3019 | -0,2184 | 0,0859 | - |
| V2i | 0,0505 | 0,0911 | 0,0477 | 0,0074 | - |
Продолжение таблицы 3
| L | |||
| Vi | 0,2626 | -0,1625 | -0,3045 |
| V2i | 0,0690 | 0,0264 | 0,0927 |
5.3 Вычисляем оценку среднего квадратического отклонения результатов наблюдений  :
:
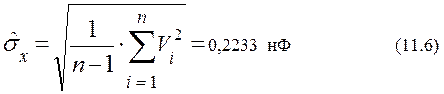
5.4 С помощью критерия грубых погрешностей (критерий «трёх сигм») проверяем наличие грубых погрешностей.
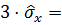 0,6699 нФ.
0,6699 нФ.
Грубые погрешности отсутствуют.
6. Определяем оценку среднего квадратического отклонения результата измерения  из выражения:
из выражения:

7. Выдвигаем гипотезу о принадлежности результатов наблюдений нормальному распределению и проверяем эту гипотезу.
В решаемой задаче n = 17. Поэтому принадлежность результатов наблюдений к нормальному распределению проверяем по составному критерию.
Критерий 1. Вычисляем смещённую оценку среднего квадратического отклонения по формуле [2]:
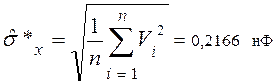 (11.8)
(11.8)
Вычисляем параметр
 (11.9)
(11.9)
Результаты наблюдений можно считать распределенными нормально, если
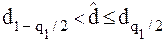 , где
, где 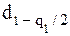 и
и 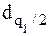 - квантили распределения, причем
- квантили распределения, причем
q1 - заранее выбранный уровень значимости критерия. Выбираем уровень значимости q равным 5 %. Находим 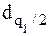 = 0,8884,
= 0,8884, 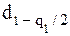 = 0,7236. Сравнивая полученное значение
= 0,7236. Сравнивая полученное значение 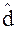 с этими величинами, делаем вывод о том, что по критерию 1 результаты наблюдений распределены по нормальному закону.
с этими величинами, делаем вывод о том, что по критерию 1 результаты наблюдений распределены по нормальному закону.
Критерий 2. Этот критерий используется дополнительно для проверки «концов» распределений.
Гипотеза о нормальности по критерию 2 не отвергается, если не более m разностей Vi превзошли значение  , где верная квантиль распределения нормированной функции Лапласа отвечает вероятности P/2. [2]
, где верная квантиль распределения нормированной функции Лапласа отвечает вероятности P/2. [2]
Для решаемой задачи выбираем уровень значимости q2 = 5% и для n = 17 находим P = 0,98 и m = 1. Тогда, обращаясь к таблице значений нормированной функции Лапласа ф(z), находим ZP/2 = 2,33. Отсюда 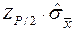 = 0,5203 нФ.
= 0,5203 нФ.
Согласно критерию 2 не более одной (m = 1) разности Vi могут превзойти значение 0,5203 нФ.
По данным, приведенным в таблице 3, видим, что ни одно V не превышает критическое значение. Следовательно, критерий 2 выполняется.
Таким образом, с уровнем значимости q £ q1+ q2 = 0,1 гипотеза о нормальности полученных данных согласуется с данными наблюдений.
8. По заданной доверительной вероятности Pд и числу степеней свободы (n-1) распределения Стьюдента определим коэффициент t. [2]
Для нашей задачи (P = 0,95 и n-1 = 16) значение t = 2,120.
Рассчитываем доверительные границы случайной погрешности результата измерения
 2,120×0,0542 = 0,1148 нФ (11.10)
2,120×0,0542 = 0,1148 нФ (11.10)
9. Записываем результат измерения.
При симметричной доверительной погрешности результаты измерений представляют в виде 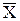 ±
±  , Pд.
, Pд.
При этом значащих цифр в  должно быть не более двух, а числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности
должно быть не более двух, а числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности  .
.
Результат измерения записываем в следующем виде:
С = (15,96 ± 0,12) нФ; Pд = 0,95 (11.11)
Ответ: С = (15,96 ± 0,12) нФ; Pд = 0,95. [1]
№12
В процессе обработки результатов прямых измерений напряжения определено: среднее арифметическое значение этого напряжения 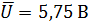 , среднее квадратическое отклонение среднего арифметического
, среднее квадратическое отклонение среднего арифметического 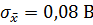 , границы неисключенных остатков двух составляющих систематической погрешности
, границы неисключенных остатков двух составляющих систематической погрешности 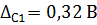 и
и 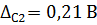 .
.
Необходимо определить доверительные границы суммарной погрешности результата измерения и записать его в соответствии МИ 1317-86 или ГОСТ 8.207-76. Значение доверительной вероятности. При расчётах полагать, что случайные погрешности распределены по нормальному закону, а число наблюдений существенно больше 30.
Date: 2015-10-19; view: 448; Нарушение авторских прав