
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема Чебышева
|
|
Пусть ξ1, ξ2, ξ3, …, ξn - попарно независимые случайные величины, имеющие конечные дисперсии. Тогда вероятность того, что среднее арифметическое случайных величин отклонится от среднего арифметического их математических ожиданий по модулю на величину меньшую ε, стремится к 1 при неограниченном увеличении n:  .
.
Сущность теоремы Чебышева состоит в следующем: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое большого числа случайных величин с большой вероятностью принимает значение, близкое к среднему арифметическому их математических ожиданий.
Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое. Итак, среднее арифметическое достаточно большого числа независимых случайных величин утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем они взаимно погашаются.
Теорема Ляпунова (центральная предельная теорема)
Рассмотрим случайные величины ξ1, ξ2, ξ3, …, ξn и найдем закон распределения их суммы при неограниченном увеличении n:
ζn= ξ1+ξ2+ξ3+…+ξn. Оказывается, что закон распределения такой суммы близок к нормальному закону. Соответствующее утверждение называется центральной предельной теоремой. Ее строгое доказательство впервые было дано русским математиком А. М. Ляпуновым.
Теорема Ляпунова (центральная предельная теорема)
Если случайная величина ζn представляет собой сумму большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то ζn имеет распределение близкое к нормальному: пусть ζn=ξ1+ξ2+ξ3+…+ξn, An=Mζn=Mξ1+Mξ2+Mξ3+…+Mξn, Bn=Dζn=D(ξ1+ξ2+ξ3+…+ξn)=Dξ1+Dξ2+Dξ3+…+Dξn, то 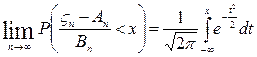
Контрольные вопросы:
1. Сформулируйте лемму Чебышева. Приведите пример ее использования.
2. Какое неравенство называется неравенством Чебышева? Приведите пример его использования.
3. Сформулируйте теорему Чебышева.
4. Сформулируйте теорему Ляпунова.
Литература:
1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.
2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.
3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.
4. Гмурман В. Е. Руководство к решению задач по теории вероятностей и магматической статистике. - М.: Высшая школа, 2005. – 400 с.
5. Гмурман. В.Е Теория вероятностей и математическая статистика. - М.: Высшая школа, 2005.
6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.
7. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.
8. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.
Date: 2015-10-18; view: 630; Нарушение авторских прав