Рассмотрим примеры сочетаний

Если покупатель оплачивает сделанную в магазине покупку, то совокупность передаваемых кассиру денег может рассматриваться как:

a) сочетание без повторений, если оплата осуществляется только банкнотами, каждая из которых имеет уникальный номер;

b) сочетание с повторениями, если оплата осуществляется монетами, среди которых могут встречаться неотличимые монеты одного достоинства.

Выведем формулы для определения числа сочетаний из n по m с повторениями и без повторений.

1. Число сочетаний без повторений из n по m.

Пусть D это некоторое множество, состоящее из n элементов. Рассмотрим все размещения без повторений из n по m, составленные из элементов этого множества. Число таких размещений равно .

Компоненты каждого такого размещения определяют некоторое сочетание без повторений из n по m, составленное из элементов этого размещения. При этом размещения, отличающиеся лишь порядком вхождения значений, образуют одно и то же сочетание.

Поскольку размещения, соответствующие одному и тому же сочетанию являются перестановками элементов этого сочетания, то всякое сочетание порождается m! различными размещениями. Обозначим число сочетаний из n по m без повторений как .

Поэтому имеет место равенство m! = .

Следовательно, справедлива следующая формула для числа сочетаний без повторений: = .

Пусть D - это произвольное множество, содержащее n элементов. Тогда число m -элементных подмножеств этого множества равно . Значит число всех различных подмножеств данного множества равно + +... + .

С другой стороны, поскольку число подмножеств n -элементного множества равно 2 ⁿ, то для сочетаний без повторений справедливо равенство:

+ +... + = 2 ⁿ.

Упражнение

Используя комбинаторные доводы доказать справедливость равенств:

1) (1 - x) ^r = 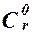x⁰ +... + (- 1) ⁱ xⁱ +... + (- 1) ^r x^r.

2) = .

2. Число сочетаний с повторениями из n по m.

Пусть D = { a ₁,..., a _n } - некоторое множество. Сочетания с повторениями, содержащие по m элементов этого множества, будем представлять двоичными последовательностями длины n + m - 1, составленными из m нулей и n - 1 единиц.

Двоичная последовательность, сопоставляемая отдельному сочетанию, состоит из n групп последовательно идущих нулей разделенных, n - 1 единицами.

В i -й группе нулей, отсчитываемой слева направо, столько нулей, сколько экземпляров элемента a _i входит в выбранное сочетание. Если некоторый элемент не входит в сочетание без повторений ни одного раза, то соответствующая ему группа нулей окажется пустой.

Например, если A = { a ₁, a ₂, a ₃, a ₄}, то сочетание с повторениями, содержащее 2 элемента a ₁, 3 элемента a ₂ и 2 элемента a ₄ представляется двоичным набором:

(0 0 1 0 0 0 1 1 0 0).

Покажем, что определенное ранее соотношение между сочетаниями с повторениями из n по m и двоичными последовательностями длины n + m - 1, содержащими по m нулей, является биективным.

Всякая двоичная последовательность длины n + m - 1, содержащая m нулей, разбивается входящими в неё единицами на n последовательно идущих групп нулей, определяющих количества вхождений элементов a ₁,..., a _n в m элементное сочетание с повторениями. Следовательно, соотношение сочетаний с повторениями и двоичных последовательностей является сюрьективным.

Покажем, что если a = s₁,..., s_m+n-1 и b = d₁,..., d_m+n-1 - две разные двоичные последовательности, то они представляют разные сочетания с повторениями. Пусть V₁,..., V_n и W₁,..., W_n - последовательности групп нулей разделенных единицами в последовательностях a и b. Тогда найдется такое i, что V _i ¹ W _i. В противном случае a и b оказываются равными. Следовательно, соотношение сочетаний с повторениями и двоичных последовательностей является инъективным.

Поэтому, число сочетаний с повторениями из n по m равно числу рассматриваемых двоичных последовательностей.

Легко проверить, что последних ровно столько, сколько имеется различных способов выбора из n + m - 1 позиций в двоичных последовательностях, таких n - 1 позиций, в которые записываются единицы. В каждом случае остальные позиции последовательности заполняются нулями.

Число способов выбора различных n - 1 позиций, если имеется n + m - 1 разных позиций, равно: .

Для обозначения числа сочетаний с повторениями из n по m применяется запись . Поэтому справедлива формула:

= _.

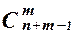Рассмотрим несколько примеров задач, приводящих к использованию сочетаний с повторениями.

1. Определить число способов составления букета из 7 гвоздик, если имеются гвоздики трех цветов.

Очевидно, что букеты как комбинаторные объекты представляют собой сочетания с повторениями из 3 по 7. Поэтому число различных букетов равно .

2. Пусть имеется n одинаковых книг. Сколько может быть способов расстановки таких книг на шести полках книжного шкафа?

Очевидно, что всякая расстановка книг на полках соответствует сочетанию с повторениями из 6 элементов по n. В таком сочетании содержатся номера полок. Число вхождений номера некоторой полки в сочетание равно количеству книг, помещенных на эту полку.

Поэтому число указанных расстановок книг на полках равно .