Критерий, определяющий расчетный случай разрушения по нормальному сечению. Связь между напряжениями в арматуре и относительной высотой сжатой зоны бетона

Критерий, определяющий расчетный случай разрушения по нормальному сечению в методе предельных усилий:

ξ=x/d – относительная высота сжатой зоны сечения

МПУ базируется на принципе пластического разрушения сечения, при котором достигается предельные напряжения в растянутой арматуре и сжатом бетоне (принцип Лолейта). На основе этого принципа расчет нормального напряжения производят, используя условия статического равновесия. Поэтому при рас­чете конструкции по методу предельных усилий необходимо прежде всего выяснить случай, по которому происходит разрушение нормального сечения.

Относительные деформации, а, следовательно, и напряжения, в растянутой арматуре зависят от высоты сжатой зоны сечения х.

εst=εcc(1/ξ-1)

В результате обработки эмпирических данных была выведена следующая зависимость:

εst=(εcu/(1-ξ0/1.1))*(ξ0/ξ-1)

εcu – предельные относительные деформации бетона при сжатии, принимаются для условий осевого сжатия = 2,5%

Величина ξ0 представляет собой относительную высоту сжатой зоны бетона с прямоугольной эпюрой напряжений, при которой деформации и напряжения в растянутой арматуре = 0, т.е. когда фактическая нейтральная линия при фактической криволинейной эпюре напряжений проходит через ц.т. арматуры и фактическая высота сжатой зоны х=d

Таким образом, величина ξ0, по существу, характеризует отклонение фактической эпюры на­пряжений в сжатой зоне сечения от принятой прямоугольной, то есть полноту эпюры напряжений в сжатом бетоне, обозначаемую далее ω0.

ω0=α-0.008fcd, α=0.85 – для тяжелого бетона

График зависимости относительных деформаций (а) и напряжений (б) в растянутой арматуре от относительной вы­соты сжатой зоны

Из данного рисунка видно, что с увелич. относит.высоты сжатой зоны, относ. деф-ции арматуры уменьшаются, проходят через 0 и затем переходят в деф-ции укорочения, которые увеличиваются до предельных деформаций укорочения бетона.

Для упругой области работы:

σs=εs+Es

Таким образом, если ξ≤ξlim, напряжения в растян.арматуре будут достигать предела текучести и разрушения будут происходить в раст.арматуре и заканчиваться в сжатом бетоне. Если если ξ>ξlim реализуем 2й случай разрушения, т.е. по сжатому бетону.

42. Расчетная схема усилий в нормальном сечении. Основные расчетные формулы

Рис. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого железобетонного элемента при расчете его прочности

Прочность изгибаемых железобетонных элементов, имею­щих как минимум одну плоскость симметрии и изгибаемых в этой плоскости следует проверять из условия M_Sd≤M_Rd,

где M_Rd=α*f_cd*S_c+ f_yd*A_sc*(d-c₁)

При этом высота условной сжатой зоны x_eff определяется из условия

f_ydA_sl = αf_cdA_cc + f_yd А_sc

При расчете изгибаемых элементов по прочности рекомендуется соблюдать условие Хeff≤ ξ_lim*d. В случае, когда площадь растянутой арматуры по конструктивным соображениям или из рас­чета по второй группе предельных состояний принята большей, чем это требуется для соблюдения условия Хeff≤ ξ_lim*d, расчет следует производить, руководствуясь положениями деформационной расчетной модели.

Для элементов, выполненных из бетона классов С²⁵/₃₀ и ниже с арматурой классов S240, S500 при Хeff≤ ξ_lim*d допускается производить расчет, принимая значения Хeff= ξ_lim*d

43. Расчет прочности изгибаемых элементов прямоугольного сечения. Решение пря­мой и обратной задачи.

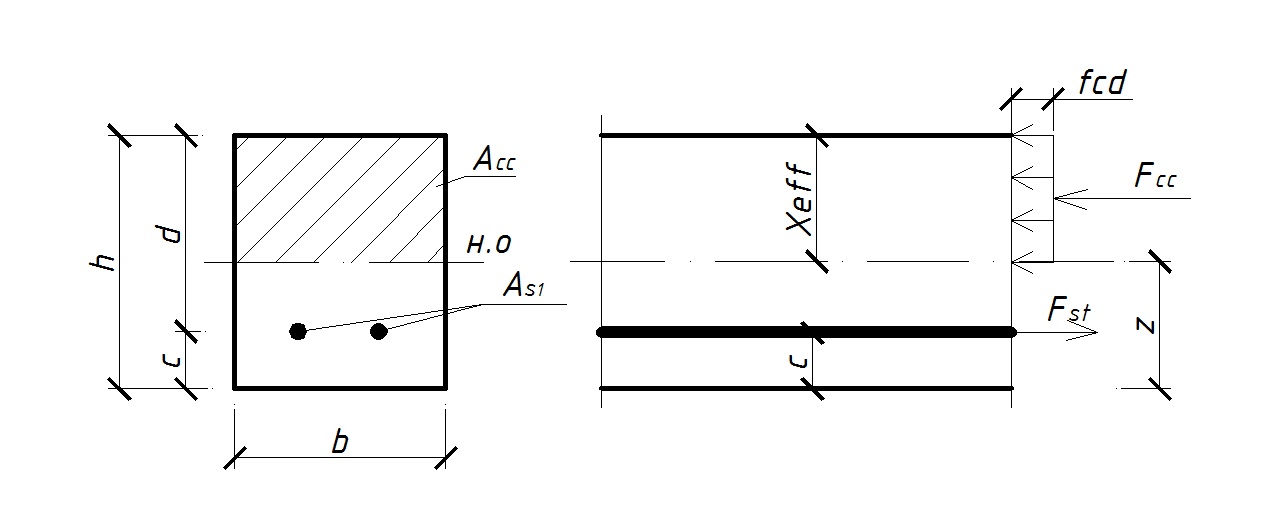1 ) C одиночным армированием

F_cc=A_cc*f_cd=b*x_eff*f_cd

(1) F_st=F_cc; f_cd*b*d*ζ=A_s1*f_yd

(2) ζ= x_eff/d; x_eff= ζ*d

(2.1) M_sd≤ M_pd=F_cc*z=f_cd*b*d* ζ*(d-0.05* x_eff)=α_m* f_cd*b*d²

(2.2) M_sd≤ M_Rd=F_st*z=f_yd*A_S1*(d-0.05* x_eff)= f_yd*d* A_S1*y_d

y=z/d=(d-0.05* x_eff)/d

Данные уравнения справедливы для случаев ζ< ζ_lim.

2) C двойным армированием

F_cc=A_cc*f_cd=b*x_eff*f_cd=b*d* ζ * f_cd

F_st= A_S1* f_yd

(1) F_st= F_cc+ F_sc

(2) M_Rd= F_cc*z+ F_sc* z_s

A_S1* f_yd= b*d* ζ * f_cd+ A_S2* f_yd(d-C₁)

2.1 α_m* f_cd*b*d²⁺ A_S2* f_yd(d-C₁)

2.2 M_Rd= A_S1* f_yd

Решение прямой задачи

Date: 2015-10-18; view: 1119; Нарушение авторских прав