Пример 1. Спроектировать контейнер в форме параллелепипеда, площадь поверхности которого была бы минимальной

Спроектировать контейнер в форме параллелепипеда, площадь поверхности которого была бы минимальной.

1. Проектные параметры X₁, X₂, X₃.

2. Ограничения. Задан объем контейнера V = 1 м.

3. ЦФ S = 2(X₁X₂+X₁X₃+X₂X₃), т.е. min S(X) X₁· X₂· X₃ = 1

Использование условия позволяет упростить ЦФ

X₃ = 1/ X₁· X₂, т.е. S = 2(X₁X₂ + 1/X₂ + 1/X₃).

Это задача безусловной оптимизации размерностью два.

§ 3.2.2 Методы решения задач оптимизации

В принципе задача оптимизации может быть решена тремя разными способами:

- аналитически;

- численно;

- методом итеративного поиска.

Первый способ решения возможен, если существуют аналитические выражения для первой и второй производной F(X) и можно аналитически решить уравнение F'(X) = 0.

Если аналитического решения уравнений F'(X)= 0 нет, то его можно получить численно методами решения системы нелинейных уравнений.

1. Поисковые методы заключаются в последовательном улучшении решения. Их схема такова: выбирают некоторое начальное допустимое решение. Чем оно ближе окажется к оптимальному, тем лучше.

2. Окружают это решение множеством сравнения и на этом множестве тем или иным способом определяют наилучший вектор X или, во всяком случае, вектор лучший, чем начальное решение; затем этот цикл вычислений повторяют, образуя окрестность улучшенного решения и т.д.

Все алгоритмы этих способов основаны на необходимых условиях оптимизации.

Существуют еще два класса вычислительных алгоритмов при поиске экстремума:

- алгоритм отсечения неоптимальных решений;

- алгоритмы, базирующиеся на достаточных условиях оптимальности.

§ 3.2.3. Задача поиска одномерного, локального безусловного оптимума.

Задача формулируется следующим образом. Найти наименьшее (или наибольшее) значение целевой функции f(X), заданной на множестве М и определить значение проектного параметра х^* Î М, при котором целевая функция принимает экстремальное значение. Если целевая функция может быть вычислена при некоторых дискретных значениях аргумента, то среди них можно выбрать экстремальное значение. Существует несколько методов решения такой задачи:

перебора, дихотомии, половинного деления, золотого сечения, квадратичной функции, Фибоначчи. Все они используют такой алгоритм.

1. Выбор начального интервала поиска [a, b] и допустимой ошибки e.
2. Выбор направления поиска внутри интервала и шага поиска Dx (стратегия поиска).
3. Вычисление значений ЦФ f(x_i).
4. Проверка условия окончания поиска. |x_i+1- x_i| < e. Если условия выполняются, переход к п.6 иначе к п.4.
5. Конец.

Рассмотрим наиболее простой метод - “ половинного деления ”.

Пусть требуется найти безусловный минимум функции f(X) одной переменной. Метод относится к последовательным стратегиям и позволяет исключать из дальнейшего рассмотрения на каждой итерации в точности половину текущего интервала неопределенности. Алгоритм уменьшения интервала основан на анализе величин функции в трех точках, равномерно распределенных на текущем интервале (делящих его на четыре равные части).

Алгоритм метода

Шаг 1. Задать начальный интервал неопределенности L₀ = [a,b], погрешность - e

Шаг 2. Положить i = k = 0

Шаг 3. Вычислить координату средней точки интервала L₀ x^c_k = (a_k + b_k)/2, длину интервала½L_2k½= b_k – a_k и значение функции f(x^c_k).

Шаг 4. Вычислить координаты точек: y_k = a_k + ½L_2k½/4, z_k = b_k - ½L_2k½/4, f(y_k), f(z_k).

Эти три точки делят равномерно исходный интервал на 4 части.

Шаг 5. Сравнить значения f(y_k) и f(x^c_k) – слева от средней точки.

а) если f(y_k) < f(x^c_k), исключить интервал (x^c_k, b_k]. Положить b_k+1 = x^c_k, a_k+1 = a_k. Средней точкой нового интервала неопределенности L₂ становится точка y_k: x^c_k+1 = y_k. Перейти к шагу 7.

б) если f(y_k) ³ f(x^c_k), перейти к шагу 6.

Шаг 6. Сравнить значения f(z_k) и f(x^c_k) – справа от средней точки.

а) если f(z_k) < f(x^c_k), исключить интервал (a_k x^c_k], положив a_k+1 = x^c_k, b_k+1 = b_k. Средней точкой нового интервала L₂ становится точка z_k: x^c_k+1 = z_k. Перейти к шагу 7.

б) если f(z_k) ³ f(x^c_k), исключить интервал [a_k, y_k), (z_k, b_k ], положив a_k+1= y_k, b_k+1 = z_k Средней точкой нового интервала останется точка x^c_k+1 = x^c _k.

Шаг 7. Вычислить длину нового интервала неопределенности½L_2(k+1)½= ½b_k+1 – a_k+1½ и проверить условие окончания поиска.

а) если ½L_2(k+1)½£ e, процесс поиска завершается и x^*Î [b_k+1, a_k+1]. В качестве приближенного решения можно взять середину интервала x^c_k+1 ;

б) если ½L_2(k+1)½> e, то положить k= k +1 и перейти к шагу 4.

Продолжать вычисления до выполнения условия ½L_2(k+1)½£ e.

ПРИМЕР 2 Найти минимум функции f(x)= 2x² – 12x на интервале [0,10], e = 1.

ð 1. L₀ = [0,10].

2. k=0.

3⁰. Вычислим x^c₀ = (0+10)/2 = 5 ½L₀½= ½ 10 - 0½, f(x^c_k) = f(5) = -10.

4⁰. Вычислим y₀ = 0 + ½10½/4 = 2.5, z₀ = 10 - ½10½/4 = 7.5, f(y₀)= -17.5,f(z₀)= 22.5.

5⁰. Так как f(y₀)= -17.5 < f(x^c₀) = -10, то положим b_k+1 = b₁ = x^c₀ =5, x^c₁ = y₀ = 2.5, a₁ = a₀= 0 и переходим к следующему шагу 7⁰.

7⁰. Получим новый интервал L₂= [ 0,5 ] ½L₂½= ½5-0½= 5> 1 k=1, переходим к шагу 4¹.

4¹. Вычислим y₁ = 0 + ½5½/4 = 1.25, z₁ = 5 - ½10½/4 = 3.75, f(y₁)= -11.875, f(z₁)= - 16.875.

5¹. Сравним f(y₁) и f(x^c₁) = f(y₀) = -17.5 Так как, f(y₁)= -11.875 > f(x^c₁) = -17.5, то перейдем к шагу 6.

6¹. Сравним f(z₁) и f(x^c₁) f(z₁) = - 16.875 > f(x^c₁) = -17.5, то положим: a₂ = y₁= 1.25 b₂ = z₁=3.75,

x^c₂ = x^c₁ = 2.5 и переходим к следующему шагу 7¹.

7¹. Получим новый интервал L₄= [ 1.25,3.75 ] ½L₄½=½3.75- 1.25½= 2.5> 1 k = 2, поэтому снова переходим к шагу 4².

4². Вычислим y₂ = 1.25 + ½2.5½/4 = 1.875, z₂ = 3.75 - ½2.5½/4 = 3.125, f(y₂)= -15.47, f(z₂)= - 17.87.

5². Сравним f(y₂) и f(x^c₂) = f(x^c₁) = -17.5 Так как f(y₂)= -15.47 > f(x^c₂) = -17.5 то перейдем к шагу 6.

6². Сравним f(y₂) и f(x^c₂) = f(x^c₁) = -17.5 Так как f(y₂)= -15.47 > f(x^c₂) = -17.5 то положим: a₃ = x^c₂ = 2.5 b₃ = b₂ = 3.75, x^c₃ = z₂ = 3.125

7². Получим новый интервал L₆= [2.5,3.75] ½L₆½= ½3.75-2.5½= 1.25> 1 k=3, переходим к шагу 4.

4³. Вычислим y₃ =2.5 + ½1.25½/4 = 2.81, z₃ = 3.75 - ½1.25½/4 = 3.43, f(y₃)= -17.93, f(z₃)= - -17.62.

5³. Сравним f(y₃) и f(x^c₃) Так как f(y₃)= -17.93 > f(x^c₃) = -17.97 то перейдем к шагу 6.

6³. Сравним f(z₃) и f(x^c₃) Так как f(z₃)= -17.62 > f(x^c₂) = -17.97 то положим: a₄ = y₃= 2.81 b₄ = z₃ = 3.43, x^c₄ = x^*Î [b_k+1, a_k+1]. = 3.125

7³. Получим новый интервал L₈= [2.81,3.43] ½L₈½= ½3.43-2.81½= 0.62 < 1 x^*Î [b_k+1, a_k+1]. Î L₈.

x^* = x^c₄ = 3.125.

Для этого уравнения оптимум можно вычислить аналитически. f ^'(x)= 4x – 12 = 0, x = 3. Значит, последний интервал надо уменьшать.

Методы дихотомии, золотого сечения и чисел Фибоначчи описаны в рекомендованной литературе.

Тестовые задания для самопроверки усвоения темы.

1. ( - это алгебраическое уравнение?

2. Перечислить шаги алгоритма поиска безусловного экстремума одномерной функции.

3. В чем идея алгоритма метода половинного деления?

4. Перечислить типы и виды экстремума функции.

5. Перечислить виды ограничений при решении задачи условной оптимизации.

§ 3.2.4 Задачи многомерной оптимизации

Как правило, целевая функция сложных технических систем зависит от многих проектных параметров,

поэтому отыскание оптимума значительно усложняется. Существует, как и для задачи одномерной безусловной

оптимизации, несколько методов отыскания многомерного оптимума.

Если уравнение целевой функции дважды дифференцируемо, то задача решается аналитически.

Если можно получить значение функции, и ее первых производных, то можно применить метод численного решен-

ния системы нелинейных уравнений.

Если можно вычислять только f(X), f' ′ (X), f " (X) только численно, то

применяют поисковые методы. Различают регулярные и случайные поисковые методы. В этом будут

рассматриваться только регулярные методы поиска.

Аналитический способ отыскания оптимума сводится к определению частных производных

целевой функции. Если приравнять их к нулю, то образуется система нелинейных уравнений.

Когда она поддается аналитическому решению, то находят значения проектных

параметров, при которых они принимают оптимальные значения.

Однако, аналитическое решение нелинейных систем уравнений редко возможно и поэтому используются

численные методы и методы поиска.

Различают 3 типа регулярных методов поиска оптимума многомерных ЦФ.

1. Методы нулевого порядка - для поиска используются только значения целевой функции F(X).

2. Методы первого порядка - кроме F(X) используются и F'(X).

3. Методы второго порядка - используются значения F(X), F'(X), F"(X).

Функцию нескольких переменных f(x) = f(x₁,x₂,...,x_n) трудно изобразить графически уже для

n=2. При n=2 функцию отображают на плоскости линиями равного уровня. Линией равного

уровня f(x) называют геометрическое место точек, в которых f(x) принимает одно и то же

значение. Так, например, для функции

f(x) = (1)

на множестве значений переменных и можно построить линии равного уровня следующим образом.

Зададимся значением функции f_i = const.

Решим уравнение (1) относительно x₂:

x₂(x₁+1)- x = f_i

.

Будем задавать значения x₁, вычислять x₂ и на пересечении x₁ с x₂ фиксировать точку, где f = const.

x₂ Для f₁ = -1

x₁ x₂

+1 0 -1

0,5 0,5

1 0

Для f₂ = 0

x₁ x₂

-1 0 +1 x₁ 0 0

0,5 0,7

1,0 0,5

0,25 0,05

0,75 0,321

- 0,25 0,083

- 0,625 1,042

-1

Рис. 4.1

Линии равного уровня функции позволяют оценить область оптимума и его характер: седло, овраг и т.д.

Для поиска оптимума многомерной функции необходимо знать её градиент и составить (затем вычислить) матрицу Гессе (H).

Градиент f(x⁰) определяется как

(2)

Матрица Гессе

, где (3)

Для функции одной переменной градиент равен первой производной, а матрица вырождается в скаляр, равный второй производной.

Найдём градиент f(x) (1) в точке .

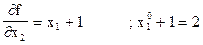
Для этой функции легко найти экстремум:

x₁ = -1; x₂ = 3.

< 0, это максимум.

Существует несколько численных методов поиска максимума функции нескольких переменных, основанных на построении улучшающей последовательности решений. Любой алгоритм построения последовательности улучшающихся решений состоит из правила перехода от решений xⁱ, полученного на I -том шаге алгоритма, к решению xⁱ⁺¹ и из правила остановки.

Для любого метода точки связаны соотношением

xⁱ⁺¹ = xⁱ + , где

- вектор направления поиска;

- характеризует величину шага;

- модуль произведения характеризует длину шага вдоль выбранного направления, и если - нормирован так, что его модуль равен 1, то - скаляр.

Правило остановки основано на неулучшаемости некоторого полученного в ходе поиска решения.

Чаще всего методы расчёта максимума функции нескольких переменных делят на три типа, в зависимости от того, какие характеристики функции используются для выбора и .

В методе нулевого порядка используются только значения функции. В этом методе используются несколько видов алгоритмов.

Для f (x₁,x₂) = 0 их можно схематически изобразить так:

x₂ x₂ x₂ x^*

M C 2

x^* x₂ x²

x’ 1

1 1’ x₁ x¹

0 0 0’

x⁰ 0’ x₀ A x⁰

x₁ x₁ x₁

Рис. 4.2 а) б) в).

На рисунках не нанесены линии равного уровня, чтобы не усложнять картинку.

В первом случае (рис.4.2а) из точки x⁰ в точку x^* можно попасть, двигаясь поочерёдно по направлениям, параллельным осям x₁ и x₂.

Это алгоритм поочерёдного изменения переменных (Гаусса-Зейделя). При движении по координате x₁ фиксируют координату x₂ и ведут одномерный поиск. Алгоритм обобщается на n переменных.

Во втором случае (рис.4.2б) используется идея параллельных касательных (сопряжённых направлений).

Из некоторой начальной точки по направлению координаты x₁ осуществляют одномерный поиск и попадают в точку x⁰. Из точки x⁰,как из начальной, методом координатного изменения аргументов находят точку x¹. Осуществляют дальнейшее движение по направлению

- такое значение аргумента функции f(x), при котором оно максимально на множестве значений. Т.е. переход из точки 1 в точку 2 осуществляется быстрее.

В третьем случае алгоритм называют симплексным. Для n=2 симплекс представляет собой треугольник.. Симплексом в общем случае (при n переменных) называют выпуклый многоугольник с n+1 вершинами, не лежащих в подпространстве размерности меньшей n. Симплекс называют регулярным (правильным), если расстояние между его вершинами одинаково.

Важным свойством симплекса является тот факт, что в результате отображения любой из вершин относительно противоположной грани, получается новый симплекс. Все вершины этого симплекса, кроме отображённой вершины, совпадают с вершинами предыдущего симплекса.

x₂ Если обозначить отображаемую вершину x⁰, две остальные

x² иx¹, а отображённую , то координату последней

x¹ x² можно определить из выражения:

x⁰ , где ; >0 множитель.

x₁

При >1 симплекс растянется;

=2 получит зеркальное отображение;

0< <1 сожмётся;

Известно несколько видов симплексных алгоритмов:

1. Алгоритм регулярных симплексов (рис.4.2в).

Строится начальный симплекс S¹.

Вычисляются значения функции f₀ в каждой из его вершин.

Находится худшее (минимальное значение f₀) из его вершин.

Производится операция отображения худшей вершины относительно противоположной грани.

Затем процедура циклически повторяется до выполнения правила остановки. Остановить поиск можно в случае, когда отображённая вершина в новом симплексе снова окажется худшей. Для уменьшения погрешности можно далее уменьшить симплекс.

2. Недлером и Мидом в 1964 году был предложен метод деформируемого симплекса, в котором симплекс меняет свою форму от цикла к циклу.

Для функции с сильно взаимосвязанными переменными, когда линии уровня функции имеют характер граблей. Хуком и Дживсом в 1961 году был предложен метод конфигураций.

Каждый цикл алгоритма состоит из 2-х операций:

- оценки характера функции f₀ вблизи текущей точки поиска;

- движения в направлении роста f₀.

При n =2

Здесь верхний индекс – номер точки, а нижний – координата.

Из исходной точки можно задавшись координатами и числом k = h построить исходный симплекс, определить координаты точек 1 и 2.

Точка 1 ( + h; -h);

Точка 2 ( -h).

При этом симплекс получится нерегулярным, т.к. сторона противоположная x⁰ будет равна 2h, а две другие

Для построения регулярного симплекса надо выбрать длину стороны h, шаг по x₁, равный h/2, а по x₂ . Тогда сторона противоположная x⁰ будет h, а две другие равны ей, т.к.

.

В этом случае

Точка 1 ( + h; -h)

Точка 2 (; )

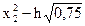Например, для функции

f (x₁ ; x₂) = x₁x₂+x₂-

в точке =1, = -1 можно построить вершину симплекса, в дальнейшем взяв приращение координат k=0,5.

x₂

-1 0,5 1 1,5

x₁

-0,5 x¹ x²

-1

x⁰

x²

a = 0,5

h = =0,87

=1, = -1

=0,5, = -0,5

=1,5, = -0,5

1

наихудшая

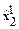= -1,

=0,5 = -1,5

Выберем сторону симплекса: а = 0.25; a / 2 = 0,125, тогда шаг по x₁= =0,43

=1 = -1

=0,875 = -0,57

=1,125 = -0,57

Затем снова повторяются вычисления функции в вершинах симплекса, пока не выполнится правило остановки.

Методы деформируемого многогранника и градиента, подробно изложены в методических указаниях по выполнению курсовой работы.

Тестовые задания для самопроверки усвоения темы.

1. А) X_ni < X_i < X_bi при i Î [1:n],

Б) ψ(X) = 0;

В) ψ(X) > 0. Где выражение для прямого ограничения ЦФ?

2. Классифицировать

Метод поиска используемые значения

а) второго порядка; 1) целевой функции F(X).

б) нулевого порядка; 2) F(X) и F'(X).

в) первого порядка; 3) значения F(X), F'(X), F"(X).

3. Неравенство F(x)-F(X^*)< 0 или F(x)-F(X^*)> 0 характеризует оптимум в точке X^*?

4. 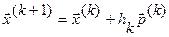, это выражение для поиска оптимума симплексным методом?

5. - это операция растяжения при симплексном методе решения задачи оптимизации?