Метод динамического программирования

Предполагается, что граф G = (X, U) не содержит контуров. Такие графы часто используются при решении задач автоматизированного проектирования, а также управления выполнением проектов с использованием методов PERT и CPM. В основе этих методов лежит построение ориентированного бесконтурного графа (сети PERT или CPM), дуги которого соответствуют некоторым элементарным задачам (этапам или операциям), составляющим проект, а их веса указывают на время, необходимое для решения отдельных задач. Кроме того, предполагается, что для любых
(x_i, x_j) Î U и (x_i, x_k) Î U задача, соответствующая дуге (x_i, x_j), должна быть закончена до начала решения задачи, изображаемой дугой (x_i, x_k). Очевидно, что ориентированный граф, который строится по указанным правилам, всегда является бесконтурным.

Алгоритмы поиска кратчайших путей в бесконтурных орграфах, основанные на методе динамического программирования, используют следующий принцип оптимальности Беллмана: "любой подпуть минимального пути является минимальным путем между соответствующими вершинами" [3].

Пусть вершины графа G = (X, U) перенумерованы таким образом, что для любой дуги (x_i, x_j) Î U всегда i < j, т. е. дуга направлена от вершины с меньшим номером к вершине с большим. Такая нумерация называется правильной и для бесконтурных орграфов всегда возможна [6].

Для построения правильной нумерации вершин используются алгоритмы топологической сортировки. Их суть заключается в следующем. Определяется некоторая вершина y Î X, из которой не исходит ни одной дуги, т. е. Г(y) = Æ. Этой вершине присваивается наибольший номер n и она удаляется из графа вместе с заходящими в нее дугами (x, y) Î U, где x Î Г^-1(y). В полученном орграфе вновь отыскивается вершина, не имеющая исходящих дуг, и ей присваивается номер n – 1. Процесс продолжается до тех пор, пока не будет образован граф, состоящий из единственной вершины x_i, которая получает номер i = 1. Варианты реализации алгоритма топологической сортировки детально описаны в работах [1, 6, 7].

Алгоритм поиска кратчайших путей m[ s, x_i ] от источника s = x ₁ до всех других вершин x_i (), представленный ниже, подобно алгоритмам 1.1 и 1.2 также использует пометки l(x_i) вершин графа.

Алгоритм 1.3 (вычисление длин кратчайших путей m[ s, x_i ]

методом динамического программирования)

Данные: бесконтурный орграф G =(X, U) с n вершинами, имеющими правильную нумерацию; выделенный источник s = x ₁; произвольные веса дуг l (x_i, x_j).

Результаты: длины l^*(x_i) кратчайших путей m[ s, x_i ] от источника s до вершин x_i ().

Шаг 1 (присвоение начальных значений)

Задать пометки l(x_i) = ¥ вершинам l(x_i) Î X \ s и l^*(x ₁) = 0 для x ₁ = s. Присвоить j = 1.

Шаг 2 (изменение пометок)

Присвоить j = j + 1 и для вершины x_j вычислить окончательное значение пометки:

, (1.4)

где T = Г^-1(x_j). При T = Æ пометка вершины x_j не изменяется.

Шаг 3 (проверка условия окончания)

Если j = n, то конец алгоритма. Иначе переход к шагу 2.

При решении задачи поиска кратчайшего пути m[ s, t ] от источника
s = x ₁ до стока t Î X \ s процесс изменения пометок завершается при достижении вершины t. В этом случае последний шаг имеет вид.

Шаг 3′ (условие окончания алгоритма 1.3 при поиске пути m[ s, t ])

Если x_j = t, то конец алгоритма. Иначе переход к шагу 2.

Таким образом, для определения пометок l^*(x_i) достаточно один раз просмотреть список вершин графа в порядке возрастания их номеров. При этом выражение (1.4) обеспечивает получение корректного результата только при правильной нумерации вершин. В целом вычислительная сложность алгоритма оценивается как O (m) операций (m - число дуг), так как каждая дуга (x_i, x_j) Î U анализируется на шаге 2 в точности один раз. Построение кратчайших путей может быть выполнено любым из способов, указанных в разделе 1.2.

Использование метода динамического программирования позволяет легко построить еще одну модификацию алгоритма поиска кратчайших путей для бесконтурных орграфов, в которой решается задача вычисления минимальных расстояний g(x_i) от каждой вершины x_i Î X \ t до стока t = x_n.

Алгоритм 1.4 (вычисление длин кратчайших путей m[ s, t ]

методом динамического программирования)

Данные: бесконтурный орграф G = (X, U) с n вершинами, имеющими правильную нумерацию; выделенный сток t = x_n; произвольные веса дуг l (x_i, x_j).

Результаты: длины g^*(x ₁) кратчайших путей m[ s, x_i ] от вершин x_i () до стока t.

Шаг 1 (присвоение начальных значений)

Задать пометки g(x_j) = ¥ вершинам x_j Î X \ t и g^*(x_n) = 0 для x_n = t. Присвоить i = n.

Шаг 2 (изменение пометок)

Присвоить i = i - 1 и для вершины x_i вычислить окончательное значение пометки:

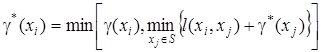, (1.5)

где S = Г(x_i). При S = Ø пометка вершины x_i не изменяется.

Шаг 3 (проверка условия окончания)

Если i = n, то конец алгоритма. Иначе переход к шагу 2.

Чтобы использовать алгоритм 1.4 для поиска пути m[ s, t ], где t = x_n и s Î X \ t, необходимо изменить условие окончания следующим образом.

Шаг 3' (условие окончания алгоритма 1.4 при поиске m[ s, t ])

Если x_i = s, то конец алгоритма. Иначе переход к шагу 2.

Трудоемкость алгоритма 1.4 определяется аналогично и также составляет O (m) операций. Эта же оценка является предельной при поиске пути m[ s, t ] и достигается в случае s = x ₁.

Существенное отличие алгоритма 1.4 состоит в обратном порядке просмотра вершин графа при расстановке пометок от стока к источнику. Для некоторой вершины x_i Î X величина g^*(x_i) определяет длину кратчайшего пути m[ x_i, t ], в отличие от пометки l^*(x_i), соответствующей длине пути m[ s, x_i ]. Поэтому при построении пути не удается использовать соотношение (1.2), так как значения g^*(x_i) предполагают получение последовательности вершин

m[ s, t ] = (s, x ⁽¹⁾, x ⁽²⁾,..., x ^(k), t)

в направлении от источника s к стоку t в соответствии с выражением вида

g^*(x_j) = g^*(x_i) - l (x_i, x_j), (1.6)

которое должно выполняться для любой дуги (x_i, x_j) Î m[ s, t ].

Сначала определяется вершина x ⁽¹⁾ Î Г(s), удовлетворяющая условию (1.6), затем x ⁽²⁾ Î Г(x ⁽¹⁾) и т.д.

При построении кратчайшего пути также возможно применение двойных пометок вида [g^*(x_i), m_i ], где m_i - вершина графа, из которой помечена x_i Î X. Вторая часть пометки обновляется при изменении g^*(x_i) по формуле (1.5) и получает значение m_i = x_j. В итоге источник s = x ₁ с пометкой [g^*(x ₁), m ₁] указывает вторую вершину x ⁽¹⁾ = m ₁ пути m[ s, t ], пометка [g(x ⁽¹⁾), m ₂] определяет вершину x ⁽²⁾ = m ₂ и т.д.

Пример 1.3. Пусть ориентированный граф, в котором отсутствуют контуры, имеет вид, показанный на рис. 1.7. Необходимо определить кратчайший путь m[ x ₁, x ₉].

Рис. 1.7. Представление графа для примера 1.3

Результаты работы алгоритма 1.3 показаны в виде вектора пометок l^*(x_i), который имеет вид:

(0, 2, 3, 1, 5, 6, 6, 9, 10).

Значения g^*(x_i), полученные по алгоритму 1.4, представлены вектором

(10, 12, 10, 9, 5, 4, 8, 5, 0).

Кратчайший путь m[ x ₁, x ₉] может быть построен по любому из этих векторов с помощью соотношения (1.2) или (1.6) соответственно и имеет вид:

m[ x ₁, x ₉] = (x ₁, x ₄, x ₅, x ₆, x ₉).

В заключение следует отметить важное свойство пометок l^*(x_i) и g^*(x_i). Для любой вершины x_i, принадлежащей кратчайшему пути m[ s, t ] в бесконтурном орграфе, всегда справедливо соотношение

l^*(x_i) + g^*(x_i) = L (m[ s, t ]), x_i Î m[ s, t ], (1.7)

где L (m[ s, t ]) = l^*(t) = g^*(s) - длина кратчайшего пути от истока к стоку.

Условие (1.7) и требование правильной нумерации вершин позволяют построить кратчайший путь, так как в последовательности m[ s, t ] вершины x_i Î m[ s, t ] всегда располагаются в порядке возрастания индексов i Î {1, 2,..., n }.

У П Р А Ж Н Е Н И Я

1.30. Обосновать необходимость правильной нумерации вершин графа при поиске кратчайшего пути методом динамического программирования.

1.31. Что показывают пометки g(x_i), приписываемые вершинам графа в алгоритме 1.4?

1.32. Составить подпрограмму построения кратчайшего пути на графе по известным значениям пометок g^*(x_i).

1.33. Разработать формальную схему алгоритма топологической сортировки вершин бесконтурного ориентированного графа.

1.34. Написать программу построения правильной нумерации вершин графа на основе алгоритма топологической сортировки.

1.35. Модифицировать алгоритм 1.3 для поиска кратчайших путей с использованием пометок вида [l(x_i), m_i ].

1.36. Модифицировать алгоритм 1.4 для поиска кратчайших путей с использованием пометок вида [g(x_i), m_i ].

1.37. Решить задачу поиска кратчайших путей m[ x_i, x ₉], , для графа из примера 1.3 по алгоритму, в котором применяются двойные пометки.

1.38. Разработать процедуру построения кратчайшего пути из источника в сток на основе соотношения (1.7).

1.39. Определить кратчайший путь из вершины x ₁ в вершину x ₉ для графа, показанного на рис. 1.8.

Ответ: значения l^*(x_i) представлены вектором

(0, 6, 4, 7, 9, 13, 15, 14, 20).

Рис. 1.8. Представление графа для упражнения 1.39

1.40. Для графа на рис. 1.8 вычислить значения g^*(x_i) при условии, что стоком является вершина x ₉.