
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод Форда - Беллмана
|
|
Данный метод обеспечивает нахождение кратчайших путей m[ s, xi ] между источником s и всеми другими вершинами xi Î X \ s для ориентированного графа G = (X, U), в котором отсутствуют контуры суммарной отрицательной длины. Веса дуг l (xi, xj) могут иметь любые значения. Метод является итерационным и основан на изменении пометок вершин графа, причем значения  (xi) в конце k -й итерации равны длинам таких кратчайших путей m[ s, xj ], которые содержат не более k + 1 дуг.
(xi) в конце k -й итерации равны длинам таких кратчайших путей m[ s, xj ], которые содержат не более k + 1 дуг.
Ниже приводится формальная схема алгоритма, реализующая метод Форда - Беллмана.
Алгоритм 1.1 (метод Форда - Беллмана)
Данные: орграф G = (X, U), имеющий n вершин, с выделенным иcточником s Î X; веса дуг l (xi, xj) для всех (xi, xj) Î U.
Результаты: длины l*(xi) кратчайших путей m[ s, xi ] для всех xi Î X \ s.
Шаг 1 (присвоение начальных значений)
Установить номер итерации k = 0. Определить множество вершин
S = Г(s). Присвоить начальные значения пометкам:

Шаг 2 (обновление пометок вершин)
Для каждой вершины xj ÎГ(S) изменить пометку:

 ,
,
где  .
.
Пометки вершин xj Ï Г(S) не изменять и присвоить
 .
.
Шаг 3 (проверка условий окончания)
а) Если k £ n - 1 и  для всех xi Î X, то получен оптимальный результат
для всех xi Î X, то получен оптимальный результат  , i =
, i =  . Конец алгоритма.
. Конец алгоритма.
б) Если k < n - 1 и  хотя бы для одной вершины
хотя бы для одной вершины
xi Î X, то выполнить переход к шагу 4.
в) Если k = n - 1 и  для некоторой xi Î X, то в графе G существует цикл суммарной отрицательной длины и задача не имеет решения. Конец алгоритма.
для некоторой xi Î X, то в графе G существует цикл суммарной отрицательной длины и задача не имеет решения. Конец алгоритма.
Шаг 4 (подготовка к следующей итерации)
Определить множество S следующим образом:
 .
.
Изменить номер итерации k = k + 1 и выполнить переход к шагу 2.
Следует отметить, что на шаге 2 множество S содержит все вершины xi графа, для которых кратчайшие пути m[ s, xi ] состоят из k дуг. Множество Tj определяет вершины из множества S, связанные дугами с xj. Если
xj Ï Г(S), то кратчайший путь из s в xj не может состоять из k + 1 дуг и поэтому пометки таких вершин l(xj) изменять не требуется. На шаге 4 новое множество S содержит все вершины, кратчайшие пути до которых содержат k + 1 дуг.
Представленный алгоритм обеспечивает получение оптимального решения. Доказательство приводится в работах [6, 10] и базируется на принципах динамического программирования и том факте, что если не существует никакого оптимального пути из k дуг, то не может также существовать никакого оптимального пути, содержащего k + 1 дуг.
Вычислительная сложность метода Форда - Беллмана имеет оценку О (n 3), т. е. в случае полного связного графа с n вершинами требуется порядка n 3 операций сложения и сравнения. Алгоритм 1.1 можно использовать и в случае неотрицательных весов дуг, но более предпочтительным является применение алгоритма Дейкстры, так как его оценка трудоемкости составляет О (n 2) операций.
Пример 1.1. Применение метода Форда - Беллмана для графа G = (X, U), приведенного на рис. 1.2 и заданного матрицей D (см. упражнение 1.12), показано в табл. 1.2. Предполагается, что источником s является вершина x 1. Окончательные значения пометок l*(xi) равны 0, 1, 4, 3, -1 для вершин xi,  , соответственно. Кратчайшие пути m[ s, xi ], где s = x 1 и
, соответственно. Кратчайшие пути m[ s, xi ], где s = x 1 и  , получены с использованием соотношения (1.2). Результаты решения задачи, включая дерево кратчайших путей, представлены на рис. 1.3.
, получены с использованием соотношения (1.2). Результаты решения задачи, включая дерево кратчайших путей, представлены на рис. 1.3.
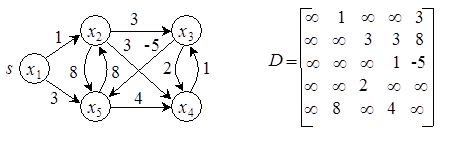
Рис. 1.2. Представление графа для примера 1.1
У П Р А Ж Н Е Н И Я
1.15. Определить особенности графовых моделей, для которых может применяться метод Форда - Беллмана.
1.16. Какое наибольшее число итераций может потребоваться при работе алгоритма 1.1? Изменится ли это значение, если веса всех дуг графа будут неотрицательными?
1.17. Решить задачу построения кратчайших путей m[ x 2, x 5] и m[ x 5, x 2] для графа, показанного на рис. 1.2.
1.18. Разработать подпрограммы формирования множеств S, Г(S) и Tj для xj Î Г(S).
1.19. Разработать подпрограммы вычисления меток вершин и проверки условий окончания итерационного процесса для метода Форда -Беллмана.
1.20. Модифицировать алгоритм 1.1 таким образом, чтобы для построения кратчайших путей использовать пометки вида [l*(xj), mj ], описанные в предыдущем разделе.
Таблица 1.2
Результаты работы алгоритма Форда - Беллмана (пример 1.1)
| Итерация | Множество S | Множество Г(S) | Вершина | Множество Ti | Пометка l(xi) |
| k = 0 | { x 2, x 5} | s = x 1 x 2 x 3 x 4 x 5 | ¥ ¥ | ||
| k = 1 | { x 2, x 5} | { x 2, x 3, x 4, x 5} | x 1 x 2 x 3 x 4 x 5 | { x 5} { x 2} { x 2 , x 5} { x 2} | min(1, 3+8) = 1 min(¥, 1+3) = 4 min(¥, 1+3, 3+4) = 4 min(3, 1+8) = 3 |
| k = 2 | { x 3, x 4} | { x 3, x 4, x 5} | x 1 x 2 x 3 x 4 x 5 | { x 4} { x 3} { x 3} | min(4, 4+2) = 4 min(4, 4+1) = 4 min(3, 4-5) = -1 |
| k = 3 | { x 5} | { x 2, x 4} | x 1 x 2 x 3 x 4 x 5 | { x 5} { x 5} | min(1, -1+8) = 1 min(4, -1+4) = 3 -1 |
| k = 4 | { x 4} | { x 3} | x 1 x 2 x 3 x 4 x 5 | { x 4} | min(4, 3+2) = 4 -1 |
1.21. Решить задачу из примера 1.1 по алгоритму, полученному при выполнении упражнения 1.20.
1.22. Составить программы поиска кратчайших путей по методу Форда - Беллмана для двух способов построения путей (см. раздел 1.2).
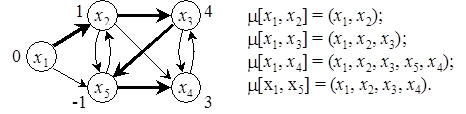
Рис. 1.3. Результаты поиска путей (пример 1.1)
1.23. Получить (машинное) решение задачи вычисления длин кратчайших путей m[ x 1, xj ],  , для графа, показанного на рис. 1.4.
, для графа, показанного на рис. 1.4.
Ответ: вектор значений l*(xi),  , имеет следующий вид:
, имеет следующий вид:
(0, -3, -11, -5, 2, -7, -1, 13, 16).


Рис. 1.4. Представление графа для упражнения 1.23
Date: 2015-10-21; view: 4422; Нарушение авторских прав