Решение. Плотность вероятности имеет вид:

Плотность вероятности имеет вид:

Построим графики функций.

Найдем вероятность того, что случайная величина примет значение, меньше 1:

Задача 5. В группе спортсменов 15 лыжников и 10 велосипедистов. Вероятность выполнить норму для лыжника равна 0,8 для велосипедиста 0,7, найти вероятность того, что наудачу выбранный спортсмен выполнит норму.

Решение. Введем полную группу гипотез

= (Спортсмен - лыжник),

= (Спортсмен – велосипедист).

Найдем вероятности гипотез по классическому определению вероятности:

,

.

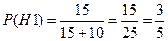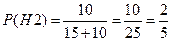Введем событие = (Спортсмен выполнит норму). Известны вероятности , .

Тогда вероятность события найдем по формуле полной вероятности

Ответ: 0,76.

Задача 6. Случайная величина x распределения по нормальному закону с параметрами m=1, σ=1. Найти

Решение. Используем формулу для нахождения вероятности попадания нормальной случайной величины в интервал:

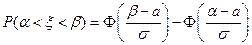, где 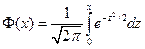- функция Лапласа (значения берутся из таблицы), - математическое ожидание, - среднее квадратическое отклонение. Получаем:

Ответ: 0,1359.

Задача 7. В первой урне 10 белых и 8 черных шаров, во второй — 6 белых и 5 черных. Из первой урны во вторую переложили один шар. Затем из второй вынимают один шар. Найти вероятность, что это будет белый шар.

Решение. Введем полную группу гипотез:

= (Из первой урны во вторую переложили белый шар),

= (Из первой урны во вторую переложили черный шар).

Найдем вероятности гипотез по классическому определению вероятности (отношение числа белых/черных шаров к общему числу шаров):

, .

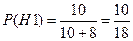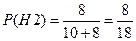Тогда во второй урне станет:

при гипотезе - 7 белых и 5 черных шаров,

при гипотезе - 6 белых и 6 черных шаров.

Введем событие = (Из второй урны извлечен белый шар). Можно вычислить условные вероятности: , .

Тогда вероятность события найдем по формуле полной вероятности

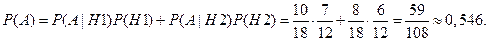
Ответ: 0,546.

Задача 8. Математическое ожидание показательно распределенной случайной величины равно 6. Написать уравнение функции и плотности распределения, построить их график. Найти вероятность попадания в интервал (0,3).

Решение. Математическое ожидание 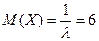, откуда .

Плотность вероятности:

График:

Функция распределения:

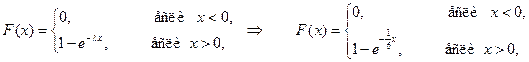
График:

Найдем вероятность:

Задача 9. Среди 20 деталей, сделанных рабочими, 5 нестандартных. Найти вероятность того, что среди взятых на испытание 6 деталей 2 будут не стандартные.

Решение. Используем классическое определение вероятности: 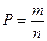, где m – число исходов, благоприятствующих осуществлению события, а n – число всех возможных исходов.

Число различных способов выбрать любые 6 деталей из 20.

Число m = различных способов выбрать 2 нестандартные детали (из 5) и еще 4 стандартные (из остальных 20-5=15 деталей).

Тогда искомая вероятность

.

Ответ: 0,352.

Задача 10. Стрелок имеет неограниченный запас патронов и ведет стрельбу до первого попадания в мишень. Вероятность попадания при одном выстреле 0,7. Найти вероятность того, что число выстрелов не превышает 5. Найти математическое ожидание и дисперсию случайной величины числа попаданий в мишень.

Решение. Пусть - дискретная случайная величина, равная числу выстрелов (числу израсходованных патронов). Она может принимать значения 1, 2, 3, 4, 5 и так далее. Найдем соответствующие вероятности.

, если при первом выстреле было попадание, .

, если при первом выстреле был промах, а при втором - попадание, .

Аналогично далее, , если при первых выстрелах были промахи, а при -ом - попадание, .

Получаем ряд распределения:

			…		…
	0,7	0,21	…		…

Математическое ожидание , дисперсия .

Найдем вероятность того, что число выстрелов не превышает 5:

Задача 11. Баскетболист делает 4 броска в кольцо. Найти вероятность того, что будет не менее 2 попаданий.

Решение. Если предположить, что вероятность попадания при одном броске равна , то искомая вероятность того, что будет не менее 2 попаданий, может быть найдена по формуле Бернулли:

Задача 12. Случайная величина x имеет плотность распределения.

f(x) =

Найти коэффициент А, математическое ожидание и дисперсию. Построить график плотности распределения.

Решение. Найдем параметр из условия нормировки: . Получаем:

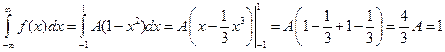, откуда находим , то есть

Найдем математическое ожидание:

(интеграл от нечетной функции по симметричному интервалу)

Найдем дисперсию:

Построим график плотности распределения:

Задача 13. На кубиках написаны буквы «к» «н» «и» «г» «а». Какова вероятность хаотично выбирая буквы сложить слово «книга»

Решение. Используем классическое определение вероятности: , где m – число исходов, благоприятствующих осуществлению события, а n – число всех возможных исходов.

способов составить различные слова из букв «к» «н» «и» «г» «а».

, так как только один из этих способов дает слово «книга».

Получаем .

Ответ: 0,0083.

Задача 14. Три стрелка производят по одному выстрелу. Вероятность попадания первого стрелка 0,8, второго 0,7, третий 0,1. Составить ряд распределения числа попаданий и найти его математическое ожидание и дисперсию.

Решение. Пусть – дискретная случайная величина, равная числу попаданий в цель, она может принимать значения 0, 1, 2 и 3. Найдем соответствующие вероятности.

Введем независимые события = ( -ый выстрел попал в цель), .

По условию даны вероятности 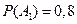, , . Вероятности противоположных событий , , .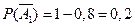

Х принимает значение 0, если все три стрелка промахнулись, то есть . Так как события независимы, получаем вероятность

.

Х принимает значение 1

или если первый стрелок попал в цель, а второй и третий – нет,

или если второй стрелок попал в цель, а первый и третий – нет,

или если третий стрелок попал в цель, а первый и второй – нет.

Таким образом, . По теореме сложения и умножения вероятностей

Аналогично для оставшихся двух случаев вычисляем:

и

.

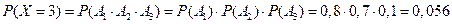Таким образом, ряд распределения случайной величины имеет вид:

	0,054	0,348	0,542	0,056

Найдем числовые характеристики случайной величины .

Математическое ожидание:

Дисперсия:

Задача 15. Из колоды в 36 карт наугад извлекают 5 карт. Найти вероятность того, что среди них ровно 1 дама.

Решение. Введем событие: = (Среди 5 взятых карт будет ровно 1 дама).

Используем классическое определение вероятности: , где m – число исходов, благоприятствующих осуществлению события, а n – число всех равновозможных элементарных исходов.

- число различных способов выбрать 5 карт из 36.

Вычислим

- число различных способов выбрать 1 даму (из 4) и еще 4 карты из колоды без дам в 36-4=32 карты.

Вероятность .

Ответ: 0,382.

Задача 16. Случайная величина равномерно распределена в интервале (-2;5). Написать уравнения плотности и функции распределения. Построить их графики. Найти математическое ожидание и дисперсию, вероятность попадания в интервал (0;5).

Решение. По условию

Найдем плотность вероятности:

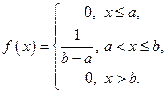то есть

Функция распределения вероятности:

то есть

Найдем математическое ожидание

.

Найдем дисперсию:

Вероятность попадания в интервал : .

Date: 2015-10-21; view: 693; Нарушение авторских прав