Векторна алгебра

Дані координати точок 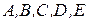. Необхідно:

1. Знайти модуль та напрям вектора у просторі.

2. Знайти кут між векторами та .

3. Знайти проекцію вектора на напрям вектора .

4. Знайти вектор , перпендикулярний до вектора 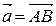і до .

5. Обчислити площу трикутника АВС.

6. Знайти висоту паралелограма, побудованого на векторах 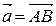і .

7. Обчислити об’єм піраміди .

8. Перевірити, чи колінеарні вектори і .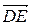

9. Перевірити, чи ортогональні вектори і .

10.Перевірити, чи належать точки до однієї площини.

Варіант 1	(0; –1; 2)	В (1; 2; 1)	С (–3; 2; 1)	D (0; 0; –1)	Е (2; 6; –3)
Варіант 2	A (–1; 3; 0)	В (2; 1; –1)	С (3; –1; 2)	D (1; –1; 3)	Е (5; 2; 2)
Варіант 3	A (0; 3; 1)	В (2; –1; 3)	С (0; 2; 1)	D (0; 1; 3)	Е (1; –1;–4)
Варіант 4	A (–1; 2; 3)	В (–1; 3; 0)	С (0; –1; 2)	D (–2;1;–1)	Е (5; 2; 3)
Варіант 5	A (2; –2; 0)	В (–2; –1;3)	С (1; –2; 0)	D (–1; 0; 1)	Е (7;–2; –5)
Варіант 6	A (–2; 0;–1)	В (1; –2; 0)	С (0; 1; 1)	D (2; 0; –3)	Е (–1; 1; 4)
Варіант 7	A (0; 1; –2)	В (2; 2; –1)	С (–1; –1;0)	D (–1;–1;0)	Е (5; 2; 3)
Варіант 8	A (3; 1; –1)	В (2; –1; 0)	С (2; 1; 0)	D (2; 1; 3)	Е (4; 0; 0)
Варіант 9	A (3; 2; 0)	В (1; –1; 1)	С (2; 0; –1)	D (2; 0; –1)	Е (6; 6; –3)
Варіант 10	A (0; –3;–1)	В (1; 0; –2)	С (–1; 0; 2)	D (0; 0; 1)	Е (–1; 1; 5)
Варіант 11	A (2; 1; –2)	В (1; 2; 3)	С (0; 3; 1)	D (–1;–2;–3)	Е (2;–5;–18)
Варіант 12	A (0; 3; –2)	В (1; –2; 1)	С (–1; 0; 3)	D (1; –2; 0)	Е (–4; 0; 4)
Варіант 13	A (2; –1; 3)	В (0; 1; –1)	С (–2; 3; 1)	D (0; –1; 0)	Е (1; –2; 2)
Варіант 14	A (0; 2; –1)	В (1; 3; –1)	С (–2; 1; 0)	D (3; 0; 1)	Е (0; –1; 3)
Варіант 15	A (1; –1; 2)	В (3; 1; –2)	С (0; 1; –1)	D (2; 3; 0)	Е (1; 2; 2)
Варіант 16	A (1; 0; 2)	В (–1; 2; 3)	С (1; 0; –3)	D (2; 1; –1)	Е (5; 3; –1)
Варіант 17	A (1;–3;–2)	В (0; –2; 1)	С (2; –3; 1)	D (–1; 0; 0)	Е (–4; 3; 9)
Варіант 18	A (1; –2; 2)	В (0; 1; 3)	С (2; 1; –1)	D (–3; 1; 0)	Е (6; 2; 0)
Варіант 19	A (2; –1; 0)	В (0; 1; 1)	С (–2; 0; 1)	D (–1;–1;–1)	Е (0; –2; 0)
Варіант 20	A (–3; 0; 1)	В (1;–2; –1)	С (0; 3; 1)	D (–2; 1; 0)	Е (1; 4; 2)
Варіант 21	A (–3;1;–1)	В (0; 2; 1)	С (–1; 3; 2)	D (2; –2; 2)	Е (–1;–3;0)
Варіант 22	A (–1;–2;–3)	В (2; 1; 0)	С (0; 1; –1)	D (–3;1;–1)	Е (–1; 1; 0)
Варіант 23	A (–1; 0; 0)	В (1; 2; –3)	С (2; 0; –1)	D (1; 3; –1)	Е (–1; 1; 2)
Варіант 24	A (0; 0; –2)	В (2; 1; –3)	С (0; 1; –2)	D (–2;–1; 0)	Е (1; 4; 3)
Варіант 25	A (–2;–1;–3)	В (–3; 1; 0)	С (2; 1; –1)	D (0; 1; 3)	Е (–2; 5; 9)
Варіант 26	A (0; 1; –4)	В (2; 2; –3)	С (–1;3; –1)	D (1; 1; 1)	Е (–2; 4; 0)
Варіант 27	A (–3;0;1)	В (–2; 1; 3)	С (0;–1; –2)	D (–1;–2;–5)	Е (1; 0; 3)
Варіант 28	A (3; 0; –2)	В (2; 1; –3)	С (–1; 0; 2)	D (2;–1;–1)	Е (2; 0; –1)
Варіант 29	A (–4; 0; 3)	В (–3; 1; 2)	С (–1; 0; 2)	D (0; –3; 1)	Е (–3; 0; 4)
Варіант 30	A (2; 2; 2)	В (3; 2; 0)	С (–1; 3;–1)	D (–2;–1;3)	Е (–1;–1;–1)

Питання для контролю знань

1. Визначення вектора. Довжина й напрям вектора.

2. Лінійні операції над векторами.

3. Проекція вектора на вісь. Вектор в прямокутній декартовій системі координат.

4. Скалярний добуток, його властивості. Кут між векторами.

5. Векторний добуток, його властивості. Площа трикутника.

6. Змішаний добуток, його властивості. Об'єм піраміди.

Date: 2015-10-21; view: 293; Нарушение авторских прав