
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение обратной геодезической задачи
|
|
 Целью решения обратной геодезической задачи является вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. То есть при известных координатах точек А (XA, YA) и В (XB, YB) необходимо найти длину SAB и направление линии АВ: осевой румб rAB и дирекционный угол aAB (рис. 10).
Целью решения обратной геодезической задачи является вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. То есть при известных координатах точек А (XA, YA) и В (XB, YB) необходимо найти длину SAB и направление линии АВ: осевой румб rAB и дирекционный угол aAB (рис. 10).
Координаты точек А (XA, YA) и
В (XB, YB) определяют при решении предыдущей задачи (см. п. 1.4.2).
Данная задача решается следующим образом.
Сначала находим приращения координат
ΔX = XB – XA,
ΔY = YB – YA.
Величину осевого румба rAB определяем из отношения
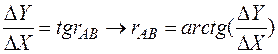 .
.
По знакам приращений координат определяем четверть, в которой располагается румб, и её название (табл. 1).
Таблица 1
Знаки приращений координат ΔX и ΔY
| Приращения координат | Четверть окружности, в которую направлена линия | |||
| I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) | |
| ΔX | + | – | – | + |
| ΔY | + | + | – | – |
Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим a AB.

Рис. 11. Осевые румбы и дирекционные углы
Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:
I четверть (СВ) r = a,
II четверть (ЮВ) r = 180° – a,
III четверть (ЮЗ) r = a – 180°,
IV четверть (СЗ) r = 360° – a.
Расстояние SAB определяем по формуле
 .
.
Для контроля расстояние SAB вычисляют дважды по формулам:
 ,
,
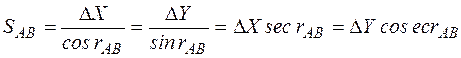 .
.
Пример. Координаты точек: А (5998.650 км, 2396.750 км);
В (6000.150 км, 2395.250 км).
Вычисляем осевой румб rAB из отношения
 ,
,
 .
.
По знакам приращений координат ΔX > 0 и ΔY < 0 определяем четверть – IV (СЗ).
Используя зависимость между дирекционными углами и осевыми румбами в IV четверти, находим дирекционный угол
 .
.
Вычисляем расстояние SAB
 км.
км.
Контроль  км,
км,
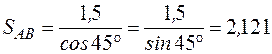 км.
км.
Date: 2015-10-21; view: 7040; Нарушение авторских прав